[논문 리뷰]Dataset Augmentation in Feature Space

논문 링크 : https://arxiv.org/abs/1702.05538

ICLR 2017 / 23.11.30 기준 447회 인용

논문 선정 이유

• 자사의 제조 데이터의 경우 시계열 데이터이지만 시계열의 특성인 t를 활용하기 애매함

• 그러한 이유 때문에, 진폭이나 진동의 반복성을 활용한 증강 기법, clipping&shuffling 같은 기존의 시계열 데이터 증강 방식 활용이 어려움

• 이 논문은 분류(회귀에서도 동작하는지는 모르겠음) 모델 한정이지만, 어떠한 데이터에도 적용 간단하고 방법이 간단하다는 점에서 논문 채택 → 시계열, 이미지, 텍스트 모두 적용 가능

• 모델의 자유도가 높음(feature map을 추출해낼 수 있는 모델이면 사용 가능)

Summary

• Objective : 데이터 증강을 통해 time-series 데이터를 분류하는 모델의 성능을 올리기 위해 데이터 $x$를 증강하는 것이 아닌 시계열 데이터를 학습한 Feature space에 증강(transform)을 주어 성능을 올림

• 기존 데이터 증강 기법들은 특정 도메인에 특화되어 다른 도메인에 적용하기 어렵다는 한계점이 존재

• 학습된 Feature space에서 간단한 transform을 적용함으로써 데이터 증강

• Method

1. Sequence Autoencoder(SA) 모델을 활용하여 Feature Space 학습

2. Feature Space에 간단한 노이즈, interpolating, extrapolating 등 다양한 방법 적용 가능

Background

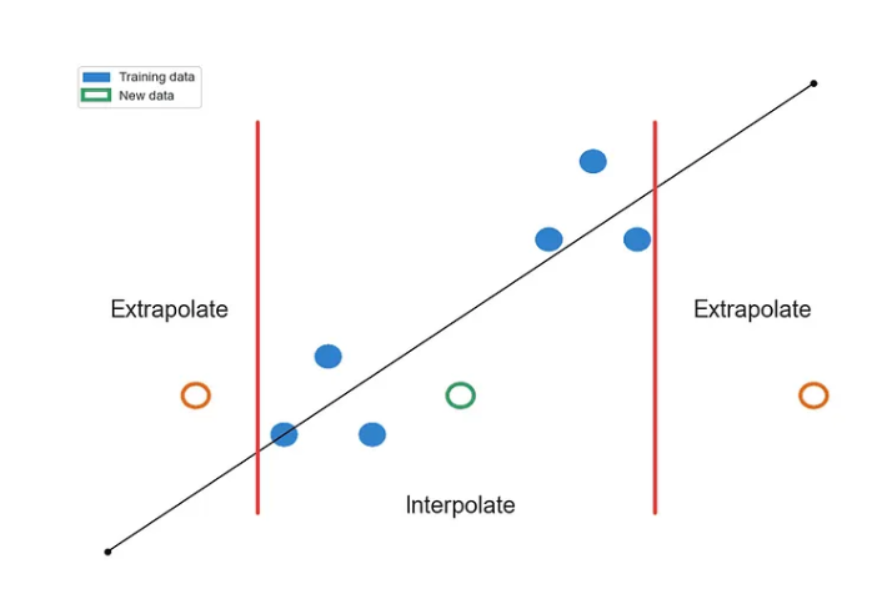
Interpolating VS Extrapolating

• 두 방식 모두 데이터 포인트를 추정하는 방식이지만, 추정하고자 하는 범위의 차이가 있음

  • Interpolating : 주어진 데이터 내부의 데이터 포인트 추정

    • ex) 11월 1일의 온도와 11월 3일의 온도를 알고 있을 때, 2일의 온도를 추정

  • Extrapolating : 주어진 데이터 외부의 데이터 포인트 추정

    • ex) 11월 1일, 2일, 3일의 온도를 알고 있을 때, 4일의 온도나 그 이후의 온도를 추정

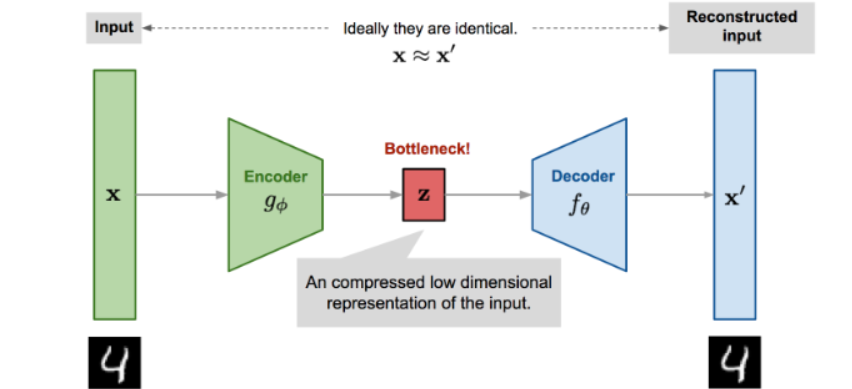
AutoEncoder

• 차원축소 혹은 Generative model로서 활용

• Reconstructed input을 생성하는 과정에서 노이즈나 크기 등의 제한을 줌

• 기존의 데이터 x와 Autoencoder를 통해 생성된 x’ 의 차이를 줄이는 방향으로 학습 진행

• $L_{AE}(\theta, \phi) = \frac{1}{n}\sum_{i=1}^{n}(x^{(i)}-f_\theta(g_\phi(x^{(i)})))^2$
  

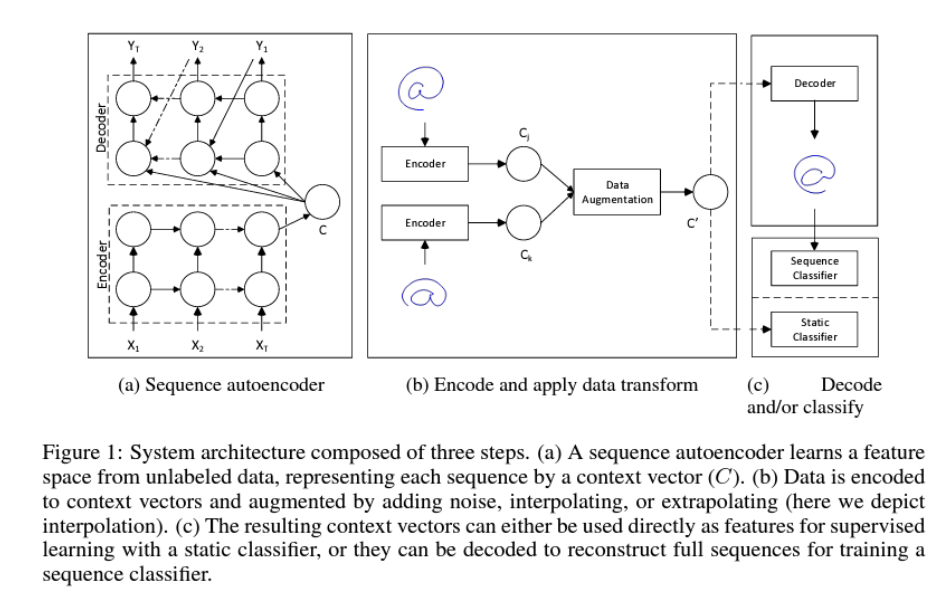
Model

• 가변하는 input과 라벨링이 되지 않은 데이터에 대해 feature 학습이 가능한 Sequece Autoencoder 활용

• 인코더&디코더 구성 요소 : LSTM

Method

1. 라벨링이 되어있지 않은 데이터에 대해서 sequence autoencoder는 feature 학습 → Context Vector(C) 생성

2. 생성된 context vector에 대해 noise, interpolating or extrapolating (논문에서는 interpolating 서술) 적용

3. Transform context vector는 바로 분류 모델의 인자로 활용되어지거나, 디코더를 통과한 reconstruct vector를 활용하여 분류 모델의 인자로 활용될 수 있음

• $y_0 = f(s_0, c)$
• $y_t = f(s_{t-1}, y_{t-1}, c)$
• $f$ : LSTM function, $s$ : state of the LSTM(both hidden, cell state), $c$ : context vector, $y$ : output of the decoder

Augmentation in Feature Space

• Gaussian noise

  • 인코더를 통과한 Context vector에 간단하게 noise를 주어 augment를 할 수 있지만, 기존 original class 혹은 다른 class 들과 너무 달라질 수 있음

  • 논문에서는 모든 context vector에 대해서 평균 및 분산을 활용한 가우시안 노이즈 활용

• Interpolation

  • 노이즈가 포함된 각 context vector($c_i$)에 대해서 feature 공간 내에 있는 동일 class(K-nearest)의 context vector 쌍을 가져옴

  • $c_i'$ : 증강한 데이터, $c_i$&$c_j$ : 이웃 context vector, $\lambda$ : control the degree of interpolation(0~1)

    • 논문에서는 $\lambda$ = 0.5로 고정해서 실험

• Extrapolation

  • $\lambda$ : control the degree of extrapolation(0 ~ infinite)

  • 0.5로 고정해서 사용해도 좋은 성능을 보임

• Data augmentation이 적용된 context vector을 바로 학습하거나, 디코더를 거쳐서 새로운 sequence data를 생성하여 학습에 활용

• 디코더 활용시 sequence 길이

  • interpolation : $c_k$, $c_j$ sequence 길이의 평균

  • extrapolation : $c_j$ sequence 길이

Experiments

Sinusoids Dataset

• 실험 환경

  • Model : LSTM based sequence autoencoder

  • Dataset : 임의의 sinusoids(진폭과 시간으로 이루어진) → amplitude, frequency, phase drawn from a uniform distribution

  • dropout : 0.2

  • Optimizer : Adam

  • lr : 0.001

  • epochs : 10

• extrapolation 방식의 경우 기존의 데이터에서 확장 → 성능 향상에 도움이 됨

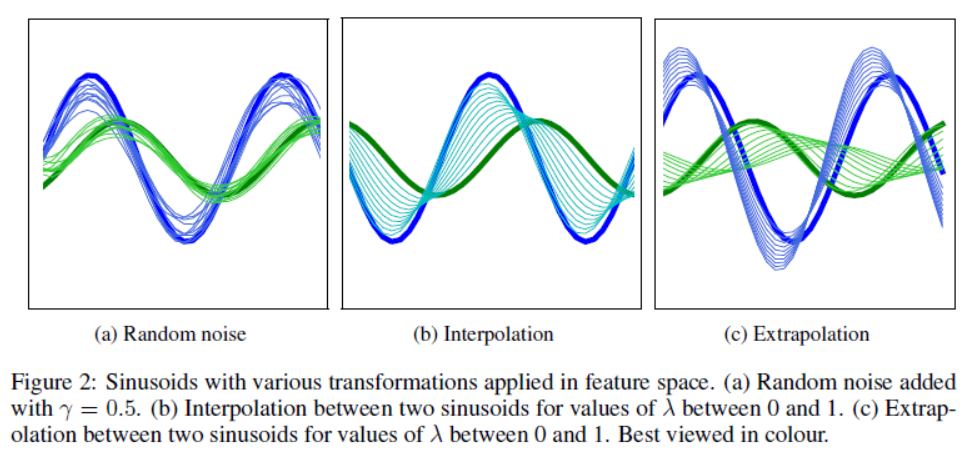
• 임의의 Sinusoids에 대해 (a)random noise 증강 (b) interpolation 증강 (c) extrapolation 증강 적용 이후(얇은 선이 증강 데이터)

• 추가 실험 결과는 논문 참조
  • 고차원 데이터일수록 Extrapolation 이 성능이 제일 잘 나온다는 내용

결론

• extrapolation은 좋은 성능을 보이는 반면, interpolation이나 noise 추가는 좋은 성능을 보이지 못함

• interpolation 같은 경우 오히려 overfitting 문제를 초래할 수 있음

• extrapolation은 각 class 간의 경계가 복잡할 때에만 좋은 성능

• 고차원 데이터일 수록 class 간의 경계가 복잡하기 때문에 extrapolation 증강 방식이 좋은 성능을 보일 것이다.

• 정교하게 각 데이터 특성에 맞는 모델을 사용하여 feature 추출 후 데이터 증강 시 좋은 성능 기대