주성분분석 - Principal Component Analysis (PCA)

차원축소(Dimension Reduction)

머신러닝 모델링을 할 때 가끔 너무 많은 양의 데이터 또는 많은 피처/특성으로 인해 메모리 문제 등 곤란을 겪을 때가 있다. 또한, 데이터들의 의미를 제대로 표현하기도 어려울 수 있다. 이러한 때에, 데이터셋의 차원을 축소해 새로운 차원의 데이터로 만들어 처리를 해주는 것이 용이 할 수 있다. 이를 차원 축소(Dimension Reduction)라 부른다.

차원 축소(Demensianlity Reduction)를 하는 이유에 대해 좀 더 알아보자면:

1. 시각화
   컴퓨터가 일반적으로 표현할 수 있는 시각화 과정은 x,y축 그리고 z축 까지의 2차원 혹은 3차원의 공간을 표현할 수 있다고 한다. 차원 축소를 3차원 이하로 하게 된다면 시각적으로 데이터를 압축하여 표현하기도 용이하다. 또한, 3차원이 넘어간 그래프는 우리의 눈으로 볼 수 없다. 따라서, 차원 축소를 통해 시각화하여 데이터 패턴을 쉽게 인지 할 수 있게된다.

2. 노이즈 제거
   불필요한 피처를 제거하여 노이즈를 제거 할 수 있다.

3. 메모리 절약
   불필요한 피처를 제거하여 데이터 처리에 필요한 메모리도 절약하면서 메모리에 의미있는 정보만 담을 수 있다.

4. 퍼포먼스 향상
   차원이 증가할수록, 피처가 많을 수록 개별 피처간 상관관계가 높을 가능성도 있으며, 과적합이 발생하고 예측 신뢰도가 떨어질 수 있다. 차원의 축소로 모델 성능 향상에 기여를 할 수도 있다.

이번에는 이 차원축소와 변수추출(Feature Extraction) 기법으로 널리 쓰이고 있는 방법 중에 하나인 주성분분석(Principal Component Analysis)에 대해 알아보았다.

주성분분석(PCA)

PCA란 데이터 집합 내에 존재하는 각 데이터의 차이를 가장 잘 나타내 주는 요소를, 데이터를 잘 표현 할 수 있는 특성을 찾아내는 방법으로, 통계 데이터 분석, 데이터 압축, 노이즈 제거 등 다양한 분야에서 사용되고 있다. 특히, 특성이 많을 경우 특성간 상관관계가 높을 가능성도 있는데, 선형 회귀와 같은 선형 모델에서는 입력한 변수들간의 상관관계가 높을 것으로 인해 다중공선성 문제로 모델의 예측 성능이 저하 될 수 있기 때문에 꼭 필요한 과정이라 할 수 있다.

PCA는 서로 상관성이 높은 여러 변수들의 선형조합으로 만든 새로운 변수들로 요약 및 축약하는 기법으로, 데이터의 분산(variance)를 최대한 보존하면서 직교하는 새 기저(축)을 찾아 고차원 공간의 표봄들을 선형 연관성이 없는 저차원 공간으로 변환해 준다. 간단하게, 가장 높은 분산을 가지는 데이터의 축을 찾아 차원을 축소하는데, 이것이 PCA의 주성분이 되는 방식이다.

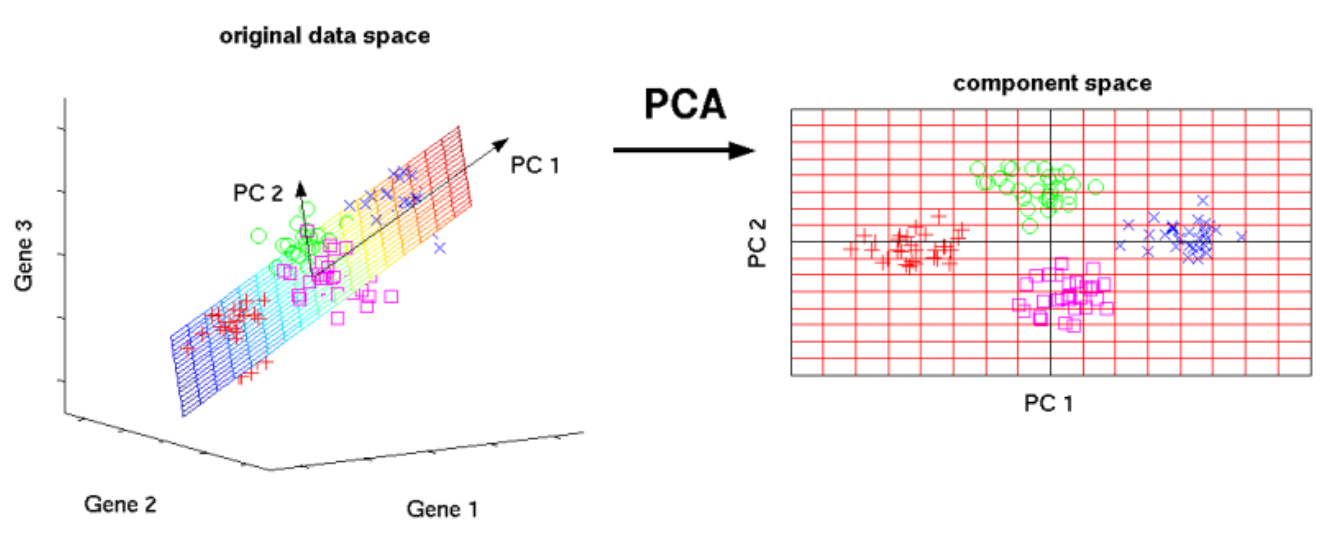
변수추출(Feature Extraction)은 기존 변수를 조합해 새로운 변수를 만드는 기법으로 변수선택(Feature Selection)과 구분해야 한다.

간단하게 데이터를 만들어 살펴보자.

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style('whitegrid')

rng = np.random.RandomState(13)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
X.shape

plt.scatter(X[:,0], X[:,1])
plt.axis('equal');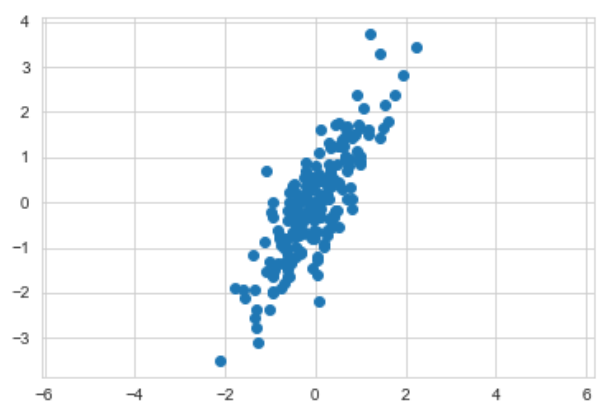

# PCA fit
from sklearn.decomposition import PCA

pca = PCA(n_components=2, random_state=0)
pca.fit(X)

# 벡터와 분산값
pca.components_

행 별로, 첫번째 주성분 pc1, 두번째 주성분 pc2를 나타낸다.

pca.explained_variance_ # 분산 설명력; 값이 클수록 좋다
# pca.explained_variance_ratio_ : %로 나타낸다

explained_variance나 explained_variance_ratio를 사용하여 분산 설명력을 조회 할 수 있다. 값이 클수록 좋다.

# 주성분 벡터를 그릴 준비
def draw_vector(v0, v1, ax=None):
    ax = ax or plt.gca()
    arrowprops = dict(arrowstyle='->',
                      linewidth=2, color='black',
                      shrinkA=0, shrinkB=0)
    ax.annotate('', v1, v0, arrowprops=arrowprops)
    
plt.scatter(X[:, 0], X[:, 1], alpha=0.4)
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)
    draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal')
plt.show();

데이터의 주성분을 찾은 다음 주축을 변경하는 것도 가능하다.

# 이번에는 n_components를 1로 두고
pca = PCA(n_components=1, random_state=13)
pca.fit(X)
X_pca = pca.transform(X)

print(pca.components_) 
print(pca.explained_variance_)

1을 주었으니 주성분도 1개가 나온다.

X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.3)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.9)
plt.axis('equal')
plt.show(); 

linear regression과 비슷한 결과처럼 보인다.

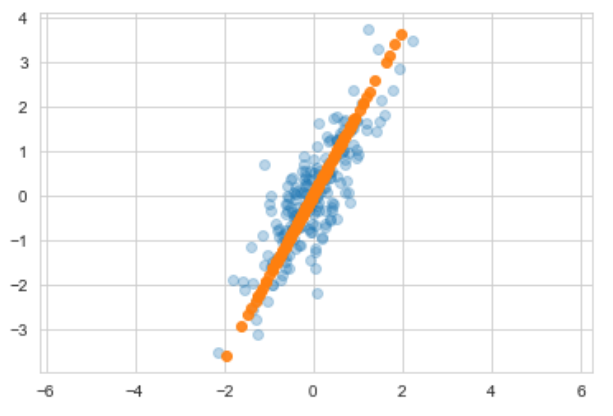
이제 Iris 데이터를 사용해 주성분분석을 진행해 보겠다.

Iris

import pandas as pd
from sklearn.datasets import load_iris

iris = load_iris()

iris_pd = pd.DataFrame(iris.data, columns=iris.feature_names)
iris_pd['species'] = iris.target
iris_pd.head(3)

# 특성 4개를 한번에 확인하기는 어렵다
sns.pairplot(iris_pd, hue='species', height=3,
             x_vars=['sepal length (cm)', 'petal width (cm)'],
             y_vars=['petal length (cm)', 'sepal width (cm)']);

특성을 pairplot으로 시각화하였다. 특성 4개를 한번에 확인하기에는 어려움이 있다.

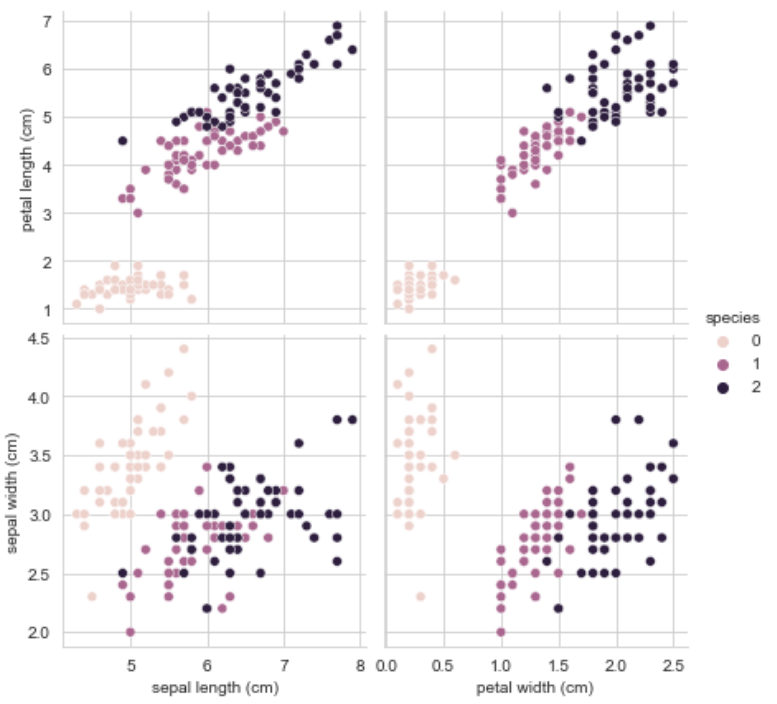
# 일단 SScaler 적용
from sklearn.preprocessing import StandardScaler

iris_ss = StandardScaler().fit_transform(iris.data)
iris_ss[:3]

일단 기존 Iris 데이터에 Standard Scaler를 적용하여 스케일링 하였다.

# pca 결과를 return하는 함수도 하나 만들어 두고
from sklearn.decomposition import PCA

def get_pca_data(ss_data, n_components=2):
    pca = PCA(n_components=n_components)
    pca.fit(ss_data)
    
    return pca.transform(ss_data), pca
    
# return 값 확인
iris_pca, pca = get_pca_data(iris_ss, 2) # 4개의 특성을 2개로
iris_pca.shape

PCA 결과 형태는 (150, 2)로 4개의 특성이 2개로 줄어든 것을 볼 수 있다. 그럼 PCA 결과를 pandas로 정리해서 보자.

def get_pd_from_pca(pca_data, cols=['pca_component_1', 'pca_component_2']):
    return pd.DataFrame(pca_data, columns=cols)
    
# 간단히 4개의 특성을 두 개의 특성으로 정리
iris_pd_pca = get_pd_from_pca(iris_pca)
iris_pd_pca['species'] = iris.target
iris_pd_pca.head(3)

두 개의 특성을 시각화해 보겠다.

sns.pairplot(iris_pd_pca, hue='species', height=5,
             x_vars=['pca_component_1'], y_vars=['pca_component_2']);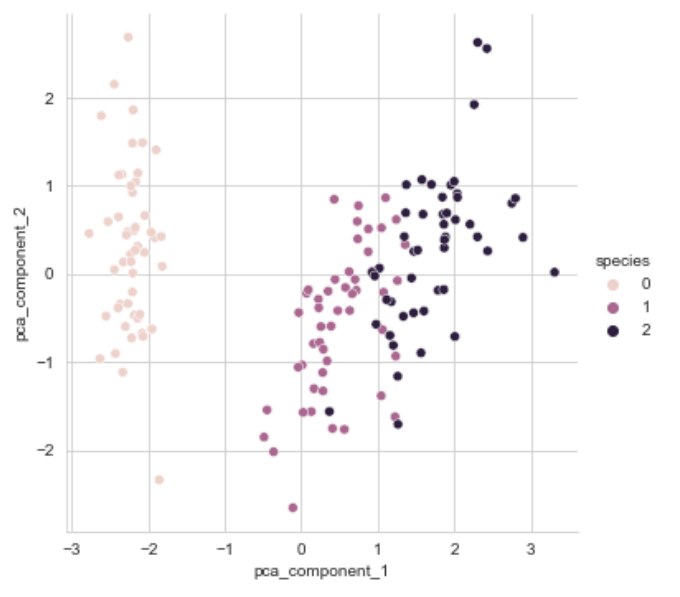

마지막으로, 4개의 특성을 모두 사용해서 randomforest에 적용해 보겠다.

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score

# 모델 평가 측정 함수 생성
def rf_scores(X, y, cv=5):
    rf = RandomForestClassifier(random_state=13, n_estimators=100)
    scores_rf = cross_val_score(rf, X, y, scoring='accuracy', cv=cv)
    
    print('Score :', np.mean(scores_rf))

# Scaling한 iris 데이터로 예측
rf_scores(iris_ss, iris.target)

우선 기존 iris 데이터를 standard scaling 적용한 데이터로 예측을 해 보았고 결과는 96%가 나왔다.

이어서 PCA 결과를 사용하여 예측을 하였다.

pca_X = iris_pd_pca[['pca_component_1', 'pca_component_2']]
rf_scores(pca_X, iris.target)

예측 결과는 91%로 기존 데이터로 예측한 결과보다는 낮지만, 데이터 차원을 감소시켰음에도 여전히 높은 예측 결과를 보인다.

이처럼, 주성분분석을 사용하여 피처/차원은 줄이되, 데이터를 나타내는 특징은 가지면서, 효율적으로 괜챃은 성능의 모델을 만들 수 있을 것 같다.

향후 모델링을 할 때에, 꼭 써보고 싶은 기법이다. 그리고 PCA 외에도 효율적이면서 효과적인 차원축소 기법이 있는지 더 알아봐야 겠다.