책은 파이썬이지만 c 언어 병행해서 공부하기

• 9/1부터 6주차로 진행하는 스터디를 정리한 것이다.
• 코딩테스트 합격자 되기 - 파이썬편 책 소개
• 인프런 동영상 링크

스터디 커리큘럼

1주차 시간복잡도 ✅
2주차 스택 ✅
3주차 큐 ✅
4주차 해시 ✅
5주차 트리 ✅
6주차 집합

9. 트리

9-1 개념

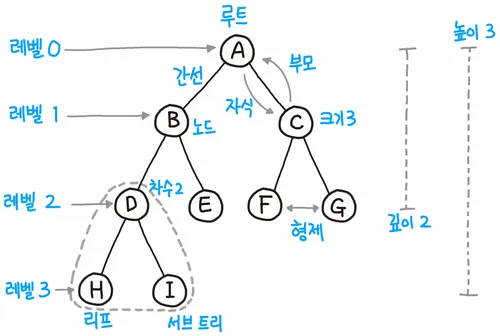
(출처: 나무위키)

• 차수: 특정 노드에서 아래로 향하는 간선의 개수

트리의 특성 활용

• 인공지능: 분류모델(decision tree, random forest 등)
• 자동완성 기능
• 데이터베이스

그래프 vs 트리 차이점

• 트리는 순환 구조를 갖지 않는 그래프
• 부모 노드에서 자식 노드를 가리키는 단방향뿐.
• 하나의 부모 노드를 갖는다. 루트는 하나.

9-2 이진 트리 표현하기

1. 배열로 표현하기

• 빈 공간이 생긴다
• 배열로 트리를 표현하면, 자식이 없거나 쓰지 않는 인덱스들은 모두 빈 값이므로 메모리가 낭비된다.(단점)
• 나쁜 표현 방법은 아님. 구현 난이도가 쉬움! 메모리가 넉넉하다면 구현 시간을 단축하는 용도로 사용하면 좋다.

2. 이진 트리 순회하기

순회: 데이터가 있을 때 그 데이터를 빠짐없이 방문하는 방법
🔹전위 순회(preoder): 현재 노드를 부모 노드로 생각했을 때,
부모노드 → 왼쪽 자식 노드 → 오른쪽 자식 노드 순서로 방문. 트리를 복사할 때 많이 사용
🔹중위 순회(inoder): 현재 노드를 부모 노드로 생각했을 때,
왼쪽 자식 노드 → 부모노드 → 오른쪽 자식 노드 순서로 방문. 이진 탐색 트리에서 정렬된 순서대로 값을 가져올 때 사용.
🔹후위 순회(postoder): 현재 노드를 부모 노드로 생각했을 때
왼쪽 자식 노드 → 오른쪽 자식 노드 → 부모노드 순서로 방문. 트리 삭제에 자주 활용.

3. 포인터로 표현하기

• 배열과 달리 인덱스 연산을 하지 않으므로 메모리 공간 낭비 x
• 구현 난이도는 조금 높음

9-3 이진 트리 탐색하기

1. 구축하기

• 데이터 크기를 따져 크기가 작으면 왼쪽 자식 위치에, 크거나 같으면 오른쪽 자식 위치에 배치하는 정렬 방식.

2. 탐색하기

• 찾으려는 값이 현재 노드의 값과 같으면 탐색 종료, 크면 오른쪽 노드 탐색
• 찾으려는 값이 현재 노드의 값보다 작으면 왼쪽 노드 탐색
• 값을 찾으면 종료. 노드가 없을 때까지 계속 탐색했는데 값이 없으면 현재 트리에 값이 없음

3. 이진 탐색 트리와 배열 탐색의 효율 비교

• 균형 이진 탐색 트리(balanced binary search tree)
  - AVL 트리 https://en.wikipedia.org/wiki/AVL_tree

  (출처: AVL tree - wikipedia)

• 레드 블랙 트리 https://en.wikipedia.org/wiki/Red%E2%80%93black_tree
  

🔹배열 탐색과 비교하면, 데이터 크기에 따라 하위 데이터 중 한 방향을 검색 대상에서 제외하므로 검색이 빠르다.

🔹시간 복잡도:

• 트리 균형이 유지된다는 전제에서 시간 복잡도는 $O(logN)$
• 균형이 맞지 않을 때는 배열과 비슷. 최악인 경우 $O(N)$

5주차 미션

트리 - 개념

문제 1.

아래와 같은 이진 트리가 주어졌을 때, 세 가지 순회 방식(전위, 중위, 후위)의 결과를 각각 작성하세요. 또한, 각 순회 방식이 어떤 경우에 유용하게 사용될 수 있는지 그 특징과 실제 활용 예시를 한 가지 이상 들어 설명하세요.

1) A를 루트로, 왼쪽 자식 B, 오른쪽 자식 C
2) B의 왼쪽 자식 D, 오른쪽 자식 E
3) C의 오른쪽 자식 F

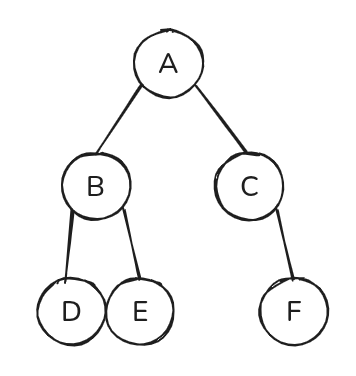
• 전위 순회 (Pre-order Traversal): A B D E C F / 트리 복사, 출력
• 중위 순회 (In-order Traversal): D B E A C F / 정렬된 순서대로 가져올 때
• 후위 순회 (Post-order Traversal): D E B F C A / 트리 삭제

문제 2.

이진 탐색 트리(BST)는 평균적으로 O(log n)의 빠른 시간 복잡도로 탐색, 삽입, 삭제가 가능하지만, 최악의 경우 O(n)까지 성능이 저하될 수 있습니다.

• 어떤 경우에 이진 탐색 트리의 성능이 최악(O(n))이 되는지 설명하세요.
  한 쪽으로 치우친 경우 연결 리스트와 동일한 구조가 된다.
• 이러한 최악의 상황을 만드는 데이터 삽입 순서의 예시를 들어보고, 그 결과로 만들어지는 트리의 형태(편향 트리, Degenerate Tree)를 설명하세요.
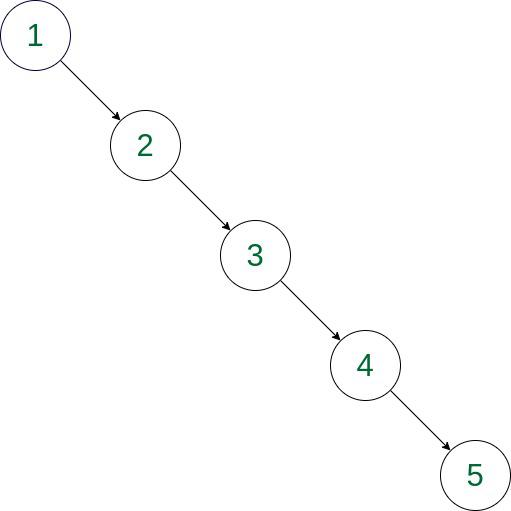
  이미 정렬된 오름차순 데이터라면, 삽입 과정이 다음과 같다.
  1 -> 루트
  2 -> 1의 오른쪽 자식
  3 -> 2의 오른쪽 자식
  4 -> 3의 오른쪽 자식
  5 -> 4의 오른쪽 자식
  

# Python implementation of above approach
class Node:
    def __init__(self, data):
        self.left = None
        self.right = None
        self.data = data

# Function to insert nodes on the right side of
# current node


def insert(root, data):
    if root is None:
        root = Node(data)
    else:
        root.right = insert(root.right, data) # 왼쪽으로 치우친 경우는 root.left
    return root

# Function to print tree


def printTree(node):
    if node is not None:
        print(node.data)
        printTree(node.right) # 왼쪽으로 치우친 경우는 node.left


# Driver code
root = None
root = insert(root, 1)
insert(root, 2)
insert(root, 3)
insert(root, 4)
insert(root, 5)

# Function call
printTree(root)

출처: geeksforgeeks

문제 3.

실시간으로 발생하는 이벤트 로그를 타임스탬프 순서대로 저장하고 검색하는 시스템을 구축한다고 가정해 봅시다. 이는 이미 정렬된 데이터가 순차적으로 계속해서 들어오는 상황과 같습니다.

만약 이 데이터를 타임스탬프를 키(key)로 사용하여 일반적인 이진 탐색 트리(BST)에 삽입한다면 어떤 문제가 발생할까요? 아래 질문에 따라 단계적으로 서술하세요.

• 데이터가 순차적으로 삽입될 때, 트리는 어떤 형태로 만들어지나요? 이 구조의 문제점을 설명하세요. (힌트: 편향 트리)
  항상 한쪽으로 치우친(왼쪽 혹은 오른쪽) 편항트리(Degenerate Tree)가 된다.
  사실상 연결 리스트와 같아져서 탐색, 삽입, 삭제 모두 O(n)
• 이러한 구조가 왜 이진 탐색 트리의 핵심 장점인 O(log n) 탐색 성능을 잃고, 마치 연결 리스트(Linked List)처럼 O(n)의 성능을 갖게 되는지 그 원인을 서술하세요.
  트리가 왼쪽 오른쪽 균형이 잡히면 높이가 log n이 되는데, 위와 같이 한쪽으로 치우치는 경우 높이가 n 에 가까워진다.
• 결론적으로, 이진 탐색 트리가 왜 '이미 정렬된 데이터'의 순차적 삽입에 비효율적인지 요약하여 설명하세요.
  정렬된 입력이 들어오면 BST는 균형을 유지하지 못한다. 사실 연결리스트나 다름이 없다.