[논문] VanillaNet: the power of Minimalism in Deep Learning

해당 논문은 Huawei에서 나온 VanillaNet 논문입니다.
동료 분께서 읽어보라고 알려주신 덕분에 읽을 수 있었습니다. 정말 저희 조직은 다 너무 좋은 분들이에요🙏
중국이 정말 무서워요...학교 다닐때 경험에 따르면 AI 분야에 엄청난 투자를 하고 있습니다. 학생들한테도 GPU를 마구마구 사용하도록 지원합니다. 그땐 몰랐어요... 그게 행복한 건지🤣

리뷰를 시작하기전에 저자 중 한 분인 王云鹤가 zhihu에 포스팅 한 것을 보았는데요. 이런게 있습니다.(https://zhuanlan.zhihu.com/p/632685158)

어떻게 VanillaNet이라는 이름을 붙이게 됐는지에 대한 이야기 입니다.
엄청 고민을 많이 하셨대요. 원래는 DeLeNet으로 하려 했다고 합니다.(세심한 꼬마친구들은 github에서 봤을거라고 말씀하셨습니다. 꼬마친구들ㅋㅋㅋ) DeLeNet은 DepthLessNet의 줄임말인데요. 막상 이름을 붙이고 보니, 너무 극단적인 것 같으셨대요. 왜냐면 한개의 레이어 수의 제한을 초월하진 못했기 때문이죠.. 그래서 또 다른 저자 분인 타오선생님께서 토론중에 VanillaNet을 제안하셨고, 다른 분들께 AlexNet을 다시 최적하여 간단, 소박, 아주 쉬운 아키텍쳐의 잠재력을 깨워서 큰 모델들이 주를 이루는 시대에서의 본 모델의 능력을 보이자고 하셨대요. (엄청난 포부..)
그리고 VanillaNet의 그들의 시작으로, 많은 것들을 다시 생각하게 하여, 어떤것이 신경망 성능을 향상 시키는것인지, depth인지, receptive field인지, 아니면 params수인지를 고민하셨다고 합니다. 게다가, 이 VanillaNet을 1년동안 개선해왔고, 현재 많은 업무에 활용중이라고 합니다.그러나 아직 발전할 가능성이 많이 남았다고 생각하십니다. 예를 들어서 pretrain 모델이 없어도, 또는 distillation이 없어도, 또는 다른 네트워크와의 결합이 없는 상황에서도, 또는 최적화를 하지 않아도 되는 그런 모델을 말이죠. 이렇게 빠른 속도로 AI가 발전한다면, 기대해볼만 하시다며 정리하셨습니다.

https://github.com/huawei-noah/VanillaNet/tree/main
https://arxiv.org/pdf/2305.12972.pdf

Introduction

해당 논문은 기존에 deep neural network들의 히스토리들을 시작으로 합니다. 그러면서 강조하는 것이 "모델의 complexity가 증가할 수 록 퍼포먼스가 증가해왔다" 입니다. 넵, 맞아요. 많은 뉴런들로 구성한 많은 layer들이나 transformer block들은 human-like task들을 수행할 수 있게 됐죠.

해당 논문의 내용을 통해 히스토리를 잠시 정리해보자면,

• AlexNet: 12 layer로 large-scale image recognition에서 SOTA를 이룸
• ResNet: shortcut connection을 통한 identity mapping으로 많은 분야에서 높은 퍼포먼스를 보임
• ViT: transformer 구조를 이미지 분야에 도입함
• Scaling Vision Transformer, Scaling transformers to 1,000 layer: ViT의 scaling laws를 만들어 성능 향상. transformer의 depth를 1000개 레이어로 scaling하여 성능 향상
• ConvNext

또, model의 complecity에 더불어 shortcut connection 얘기가 나옵니다. shortcut 없이는 34 layer의 plain network가 18 layer를 이기지 못함을 얘기하는데요.

이 shortcut 얘기를 한 이유는!! shortcut connection이 이렇게 중요함에도 불구하고 "우리는 사용하지 않았다"를 얘기합니다. shortcut이 off-chip memory traffic을 많이 소비한다는 것도 넌지히 얘기하면서 말이죠.

그러면서, VanillaNet을 아래 처럼 간단히 정리해줍니다.

• 제한된 환경에서도 학습이 가능함
  • 엄청나게 큰 depth를 사용하지 않음
  • shortcut을 사용하지 않음
  • 복잡한 self-attention을 사용하지 않음
• 간단한 구조로 생길 수 있는 challenge들을 포괄적으로 분석함
• "deep training"전략을 사용함
  • 인퍼런스 속도를 늘리지 않고도, easy-merging을 위해서 non-linear 레이어들을 없앰.
  • network의 non-linearity를 augment하기 위해서, 효율적인 series-based function을 넣음
• 이로써, 덜 복잡하지만 성능 좋은 NN을 만들어냄.

Vanilla Neural Architecture

VanillaNet의 구조에 대해서 조금 더 자세히 얘기를 시작해봅니다.
우선, VanillaNet은 수십년동안 연구자들이 만들어 온 NN의 기본 구성을 따라갑니다. 그 consensus는 바로 3 단 구조인데요. 아래와 같습니다.

• stem block: input 이미지의 3개 채널을 downsampling을 통해서 다수의 channel로 만드는 부분
• main body: 유용한 정보들을 학습하는 부분
  • 4개의 stage로 구성되어 있고, 각 stage는 여러 block들을 쌓은 구조
  • channel이 확장되고, width & height 감소
• FC (Fully Connected) layer: 출력 결과를 classification하는 부분

기존의 network들은, ResNet은 34 또는 50 layer, ViT는 62 layer와 같은 구성으로 다소 복잡한데요. 아무리 AI chip들이 발전해왔어도, 이러한 구조들이 speed면에서는 좋다고는 할 수 없다고 합니다. 그래서, VanillaNet은 한 stage에 하나의 layer로 매우 간단하게 만들어졌습니다..😲

VanillaNet의 구조를 6 layer로 예를 들어 자세히 살펴보면 이렇습니다.

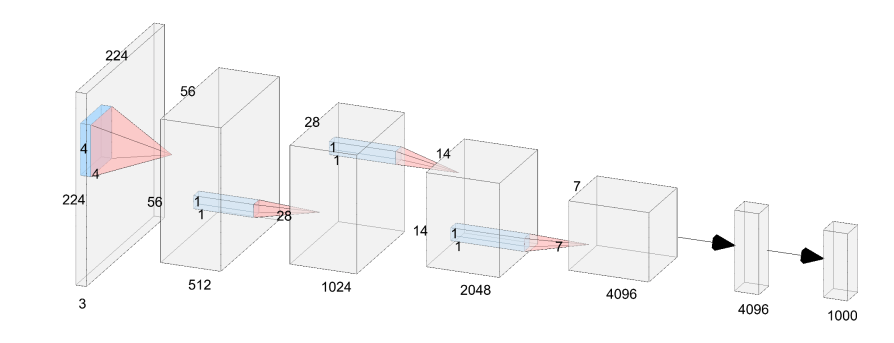
• Stem
  • stride4의 4 x 4 x 3 x C의 conv layer로 이미지의 3채널을 C채널로 만들어 줍니다.
• Main Body
  • Stage 1,2,3: stride 2의 maxpooling으로 사이즈는 줄이고, 피쳐맵과 채널 수를 두배씩 늘려줍니다.
  • Stage 4: 채널을 늘리지 않고 average pooling을 해줍니다.
• FC layer
  • 최소한의 계산량을 얻고 feature map의 정보를 유지하기 위해서, 각 conv layer의 kenel size는 1 x 1로 합니다.
  • activation function은 각각의 1 x 1 conv layer뒤에 넣어줍니다.
• 학습을 쉽게 해주기 위해서, BN(Batch Normalization)도 각각 layer에 넣어줍니다.

추가로, 저자는 shortcut을 넣어보긴 했으나, 성능 향상이 없었다고 합니다. 또한 squeeze나 excitation block과 같은 extra block이 없어서 동작하기 아주 쉬운점도 언급했습니다.

Training of Vanilla Networks

Deep Training Strategy

• 처음 학습할 때, 두개의 convolutional layer를 하나의 activation만 적용합니다.
• activation function은 학습 에포크가 증가함에 따라, indetity mapping으로 감소합니다.
• 그럼, 학습 후에는, 두 conv layer를 하나로 합치기 쉬워지고, inference 시간까지 줄일 수 있습니다.

이런 아이디어는 여기서만 쓰는 건 아니고 다른 논문에서도 많이 활용하죠.
(Acnet, Diverse branch block, Scaling up your kernels to 31x31, Repvgg) -> 약간 TODO 느낌이네요 😆

Activation Function

ReLu와 Tanh같은 Activation $A(x)$을 저자는 identity mapping으로 합칩니다. 식은 아래와 같습니다.
$A'(x) = (1-\lambda)A(x) + \lambda x$
여기서, $\lambda$는 개선된 activation fucntion $A'(x)$의 non-linearity의 밸런스를 맞추기 위한 하이퍼 파라미터 입니다. 현재의 epoch를 $\epsilon$, 학습하는 epoch를 $E$라고 한다면, $\lambda$는 $\frac{\epsilon}{E}$로 설정했고, 따라서 처음 시작할때는 $A'(x) = A(x)$겠죠. 다른 의미로 시작일때는 non-linearity가 강하다는 거죠. 반대로 학습이 진행되면서 $A'(x) = x$로 수렴하게 되는겁니다. 즉, 두 conv layer 중간에 activation function이 없다는 의미를 가집니다.

How to merge 2 conv layers

그럼, 어떻게 이런 두 conv layer를 합치는 지를 보겠습니다.

• BN과 그 앞에 있는 conv를 하나의 conv로 변환합니다.
  • conv관련
    • W, B: weight, bias
    • $C_{in},C_{out}, k$: input channel, output channel, kernel size
  • BN관련
    • $\gamma, \beta, \mu, \sigma$: scale, shift, mean, variance
  • 합쳐진 weight 와 bias는 아래와 같아집니다.
    • $W'_i=\frac{\gamma_i}{\sigma}W_i B'_i =\frac{(B_i-\mu_i)\gamma_i}{\sigma_i}+\beta_i$
    • $i$는 $i$번째 output channel입니다.
• BN과 conv를 합친 후, 두개의 1 x 1 conv를 합쳐줍니다.
  • 이때, $x$와$y$는 input, output feature
  • 그럼 conv를 다음과 같이 정의할 수 있습니다.
    • $y = W*x=W\cdot im2col(x)=W\cdot X$
  • 이를 통해, im2col operation이 간단한 reshape이 되었음을 알 수 있습니다.
• 최종으로 다음과 같이 정리 됩니다.
  • 두 conv의 weight를 $W^1,W^2$라고 한다면,
  • $y=W^1*(W^2*x)=W^1 \cdot W^2\cdot im2col(x)=(W^1*W^2)*X$

삐빅, 천재입니다....대박이죠...👏

Series Informed Activation Function

유명한 activation function RELU계열들은 deep하고 복잡한 network의 성능을 올리는데에 초점을 두었습니다. 그러나, 많은 논문에서 증명된 것 처럼, 간단하고 shallow한 network는 non-linearity의 부족함으로 인해서 충분한 연구 또한 부족했죠.
사실, NN의 non-linearity를 향상시키는 방법에는 두가지가 있습니다.
1. non-linear activation layer 쌓기
2. 각각의 activation 레이어의 non-lianearity를 향상시키기
기존의 논문들은 1번에 집중했고, 병렬 연산 능력이 초과하면 높은 latency가 생길 수 밖에 없었죠.

하나의 직관적인 아이디어로 activation layer의 non-linearity를 개선하는 것은 stacking입니다. 연속적으로 activation layer를 쌓는 것이 deep network의 주요 아이디어죠. 반대로, 저자들은 concurrent하게 activation layer를 쌓았습니다.

• concurrently stacking of $A(x)$
  • $A_s(x)=\sum^n_{i=1}a_iA(x+b_i)$
    • $A(x)$: 하나의 activation function
    • $a,b$: 단순한 축적을 피하기 위한 각 activation의 scale과 bias

위와 같은 방식은 activation function의 non-linearity 대폭 향상시킨다고 합니다.

두번째로 approximation ability를 더 풍부하게 하기 위해서, series based function이 BNET과 비슷한 방법인 input을 neighbor들로 부터 다양하게 함으로써 global 정보 또한 배울 수 있게 했습니다. 수식은 아래와 같습니다.

• $A_s(x_{h,w,c})=\sum_{i,j\in\{-n,n\}}a_{i,j,c}A(x_{i+h,j+w,c}+b_c)$
  • $h\in\{1,2,...,H\}, height, w\in\{1,2,...,W\}, width, c\in\{1,2,...,C\}, channel$

수식에서 알 수 있듯이, $n=0$일땐, $A_s(x)$가 일반 activation functiond인$A(x)$되죠. 다른 말로 하면, 기존의 activation function의 일반적인 확장으로 볼 수 있죠. 저자는 VanillaNet에서 activation function로 ReLU를 써서 GPUs에서 효율적으로 쓸 수 있었다고 합니다.

연산량으로 따지면 아래와 같아집니다.

• $O(CONV) = H$ x $W$ x $C_{in}$ x $C_{out}$ x $k^2$
• $O(SA) = H$ x $W$ x $C_{in}$ x $n^2$, $SA$: series activation
• $\frac{CONV}{SA}=\frac{H\times W\times C_{in}\times C_{out}\times k^2}{H\times W\times C_{in}\times n^2}=\frac{C_{out}\times k^2}{n^2}$

VanillaNet-B의 네번째 stage를 예로 들면 $C_{out}=2048, k=1, n=7$로, 84정도입니다. 즉, 연산량이 확 줄어드는 걸 체감 할 수 있죠 (WOW)

Experiments

Ablation study

사실 n=0일때는 일반 activation이기 때문에, 이 논문의 컨셉과는 맞지 않죠. 그렇지만 위의 표를 보면 알 수 있습니다. 위의 결과는 ImageNet dataset에 대한 결과인데요. 저자는 n=3일때가 가장 밸런스적으로 적절하다고 말합니다.

Influence of deep training

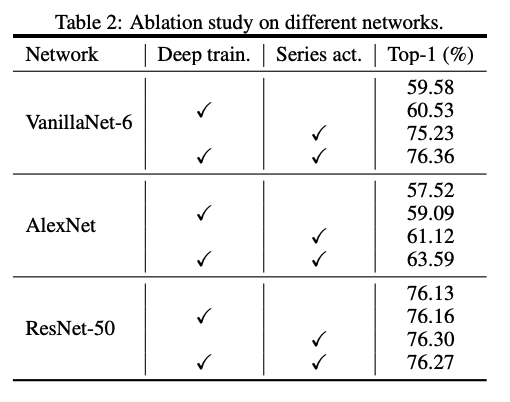
위의 표를 보면 모든 네트워크에 해당 테크닉이 성능향상을 보여주는데요. 그래도 ResNet-50을 보면 알 수 있듯이 복잡한 모델은 deep training 없이도 이미 충분한 non-linearity를 가지고 있음을 알 수 있습니다. 반대로, VanillNet처럼 간단하고 shallow한 network에는 deep training이 엄청난 효과를 주는거죠!

Influence of shortcuts

저자는 shortcut을 VanillaNet에 넣어보면서 놀라운 걸 발견했다고 합니다. 저자가 해당 네트워크의 bottleneck으로 보는것은 identity mapping이 아니라, 약한 non-linearity인데, shortcut은 activation function을 스킵하면서 depth를 줄여 이런 non-linearity를 올리지 못할 뿐만 아니라 오히려 감소시킨다고 합니다.

Visualization of Attention

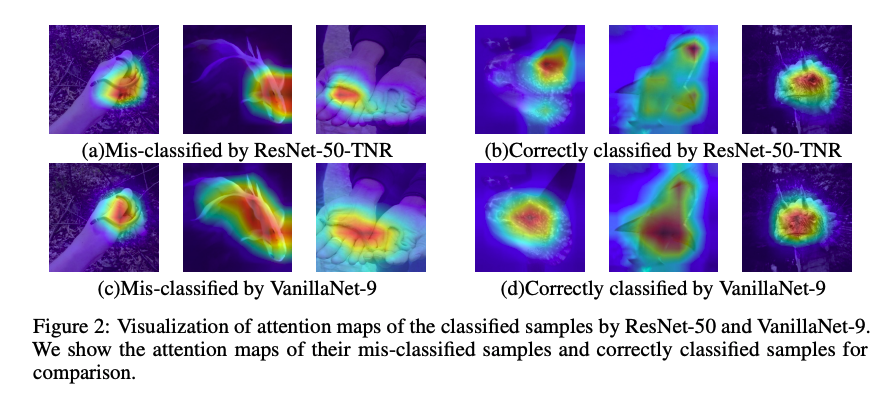
다른 네트워크들보다 더 잘 attention함을 보여줍니다.

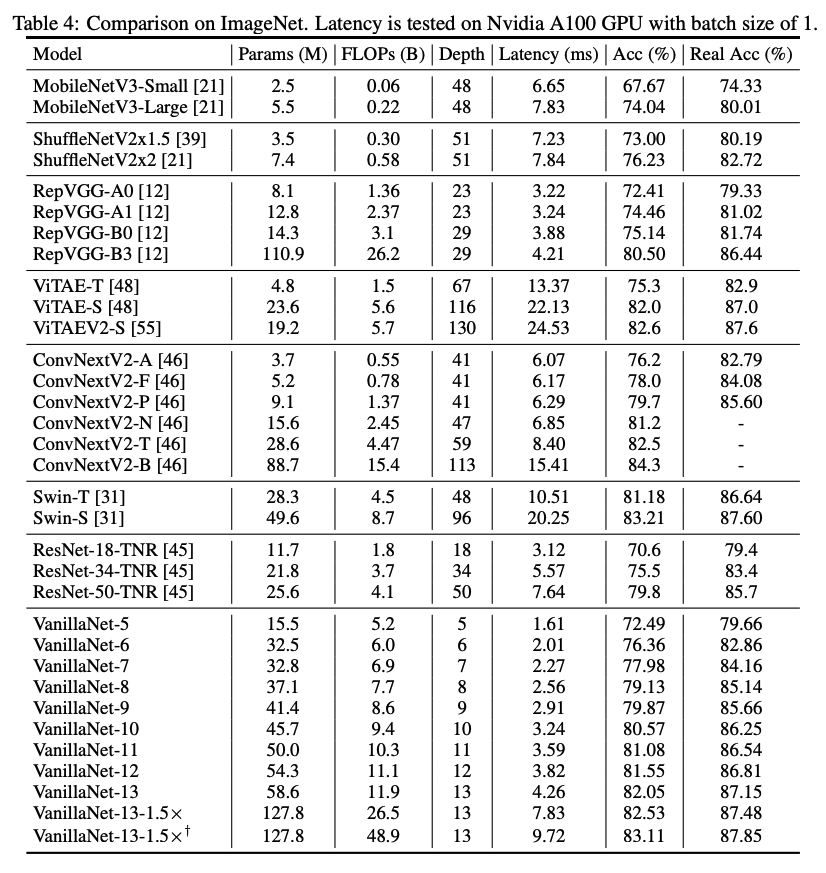
Comparison with SOTA architectures