ML [7] Bayesian Network(1)

본 포스팅은 카이스트 산업및시스템공학과 문일철 교수님의 Introduction to Artificial Intelligence/Machine Learning(https://aai.kaist.ac.kr/xe2/courses) 강의에 대한 학습 정리입니다.

이번장에서는 graphical model중에 bayesian network를 다룹니다.

확률론 복습

확률, Probabilities

• outcome이 얻어지는 상대적인 빈도(relative frequency)

조건부 확률, conditional Probability

• A라는 조건이 보장될때 B의 확률.
  $P(A=true|B=true)$

Joint Probability

• A와 B가 동시에 일어날 확률
  $P(A=true, B=true)$
  $P(X|Y)=P(X,Y)/P(Y)$

확률 연산

• Law of Total Probability
  • $P(a) = \sum_{b}P(a,b) = \sum_{b}P(a|b)P(b)$
  • $P(b) = \sum_{a}\sum_{c}\sum_{d}P(a,b,c,d)$
  • $P(c|b)=\sum_{a}\sum_{d}P(a,c,d|b)$$=\frac{1}{P(b)\sum_{a}\sum_{d}P(a,b,c,d)}$
• Chain Rule or Factorization
  • $P(a,b,c,d,....,z)=P(a|b,c,d,...,z)P(b,c,d,...,z)$
  • $P(a,b,c,d,....,z)=P(a|b,c,d,...,z)P(b|c,...,z)....P(z)$
    => factorized into a series of multiplication => chain rule
• Independence
  • $P(A,B) = P(A)P(B)$
  • $P(B|A) = P(B)$

Bayesian Network

• Graphical notation of
  • Random variables
  • Conditional independence
  • full joint distributions의 가장 compact하게 representation
• Syntax
  • 사이클이 없는(acyclic) 그래프
  • A set of nodes
    • A random variable
    • A codniational distribution gicen its parents
    • $P(X_1|Parents(X_1))$
  • A set of links
    • parents가 child에게 주는 direct influence

Components of Bayesian Network

• 질적인 요소
  • 일반적인 관계의 사전 지식
  • 데이터를 통한 learning
  • 구조적인 모습
• 양적인 요소
  • 조건부확률 테이블
  • 확률 분포
• 확률 계산에는 두 요소 모두 필요

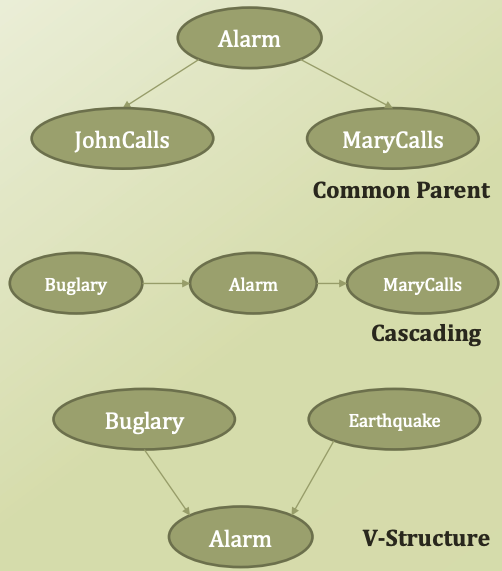
Typical Local Structures

• Common parent
• Cascading
• V-Structure
  

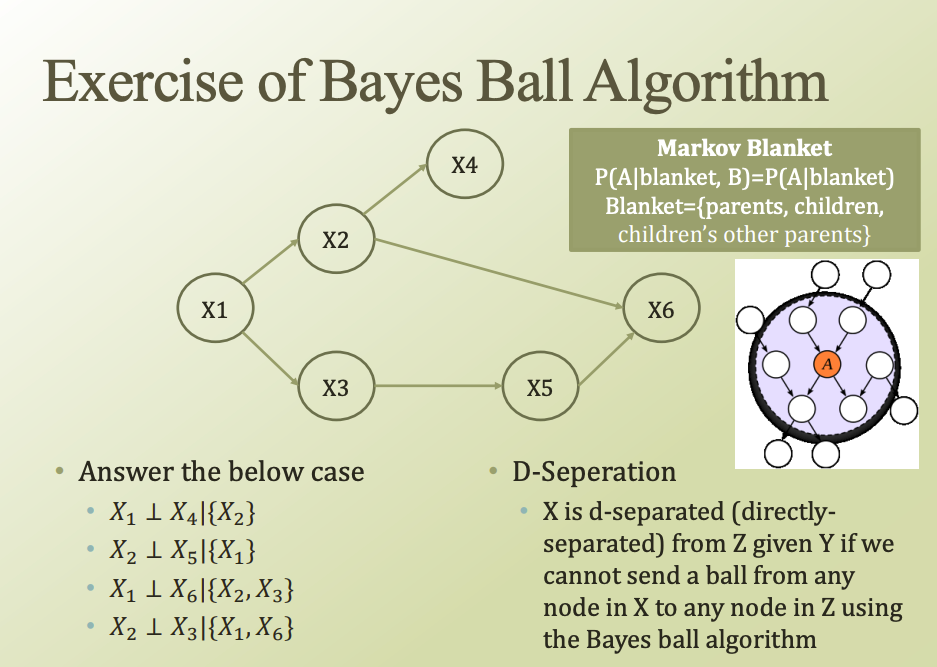
Bayes Ball Algorithm

• 목적: checking $X_A 와X_B 독립,X_C의 조건$
• 예)
  

Factorization of Bayesian Network

• Factorization Theorem
  • 주어진 Bayesian Network에서
  • 가장 일반적인 확률 분포 형태는
  • 주어진 부모 노드에 따라서 factorize된다.
  • $P(x)=\prod_i{P(x_i|x_{\pi_i})}$
  • $x_{\pi_i}:X_i$의 부모노드 집합

Plate Notation

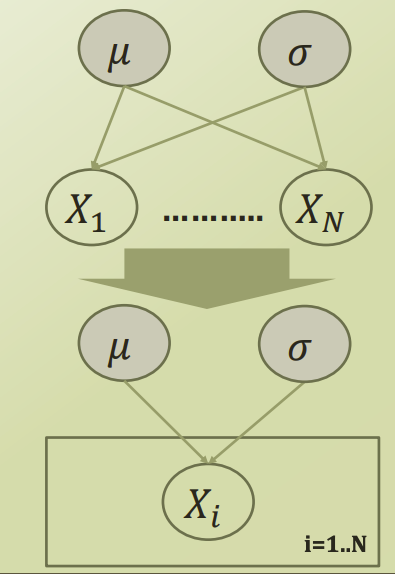
위의 그림 중 위의 네트워트를 아래 네트워크처럼 표현하는 것을 plate notation이라고 한다.