본 포스팅은 카이스트 산업및시스템공학과 문일철 교수님의 Introduction to Artificial Intelligence/Machine Learning(https://aai.kaist.ac.kr/xe2/courses) 강의에 대한 학습 정리입니다.
Bayesian Network로 해결할 수 있는 문제들
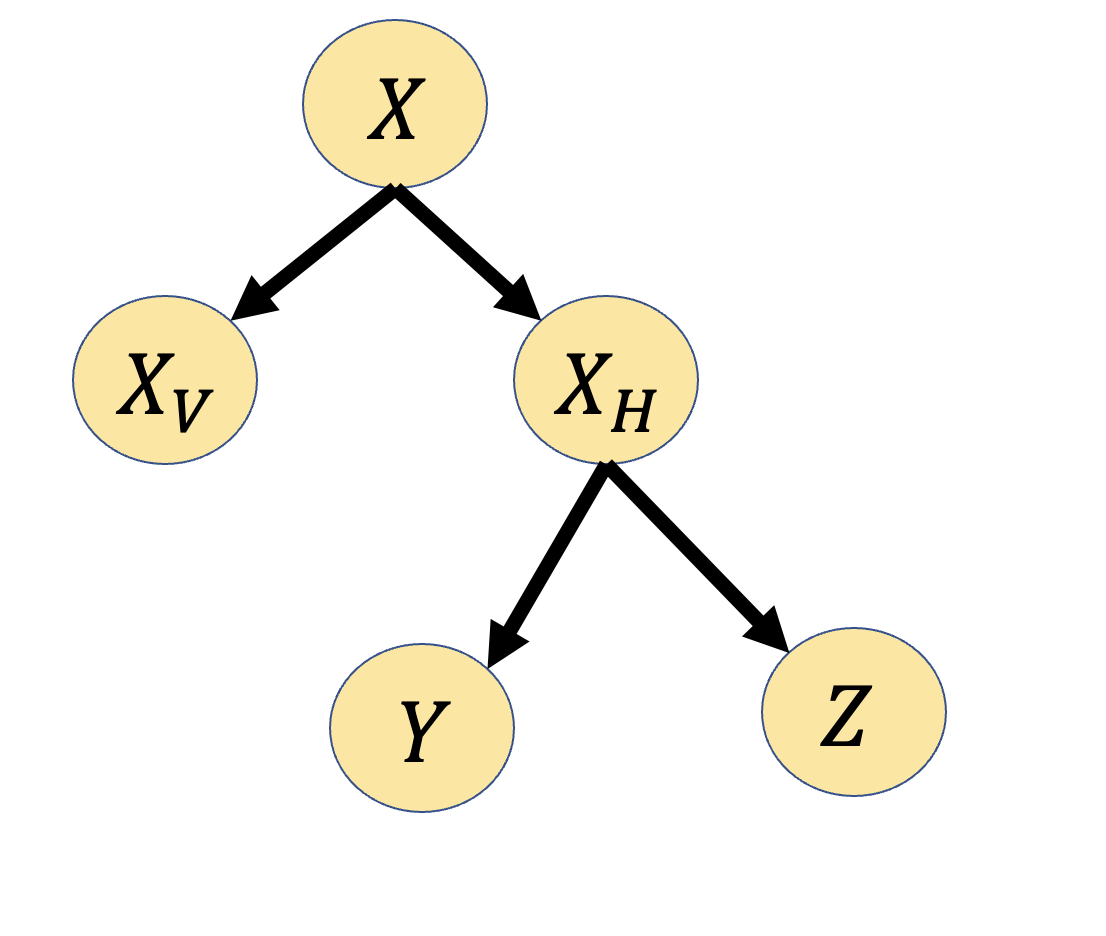
- evidence 집합이 주어졌을 때, 관심있는 Hidden variable의 conditional probability는?
- : 관심있는(Interested) Hidden variables
- : 관심없는 Hidden variables
- 일반적인 형태
- (Most probable assignment) evidence 집합이 주어졌을 때, 가장 말이되는(probable) 설명은 어떤것일까?
- 몇몇의 관심있는 variables들이 있을때,
- 관심 있는 Y에 대해서 가장 Maximize할 수 있는 assignment를 찾는 것.
- Prediction의 경우: B,E -> A
- Diagnosis의 경우: A -> b,E
Marginalization and Elimination
- Joint probability를 계산할때, 곱셈과 덧셈이 너무 많아지는 경우가 생길 수 있다.
- 따라서, summation과 독립적인 확률계산은 앞으로 옮겨 계산하는 것이 더 좋다.
- Variable Elimination
- Preliminary
- Joint probability ()
- 위 처럼 topological order
- 확률을 function으로
- Preliminary
- Variable Elimination
Undirected Graphical Model
- 우선, 강의에서 다룬 Bayesian Networks는 Directed Graphical Model의 대표적인 예 입니다.
- Bayesian Network의 특징
- directed: 방향은 있지만
- Acyclic: 순환하지 않는
- 유효하지 않은 bayesian network
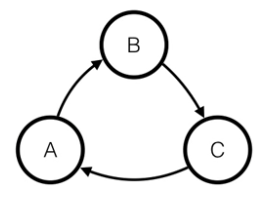
- 이 경우가 가능한 경우는 오직
- aka. directed acyclic graphs(DAGs)
-
Undirected Graphical Models
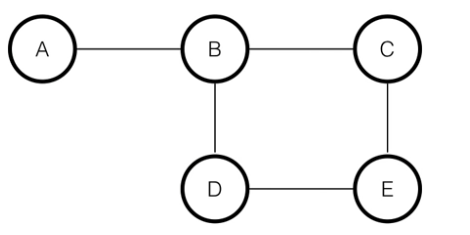
- 위 그림의 edge는 factorized probability에서 특정 factor의 potential function을 의미한다.
- 즉, 그래프의 변수들의 joint probability가 각각의 clique potential function으로 factorize된다.
- clique: 그래프 이론에서 그래프의 subset
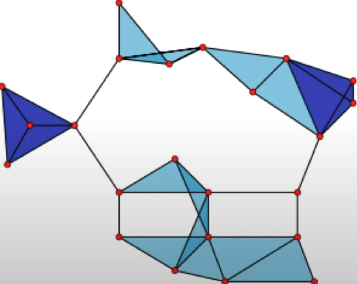
- 위의 그래프에서는 clique는 다음 그림처럼 각각의 한 묶음을 지칭한다.
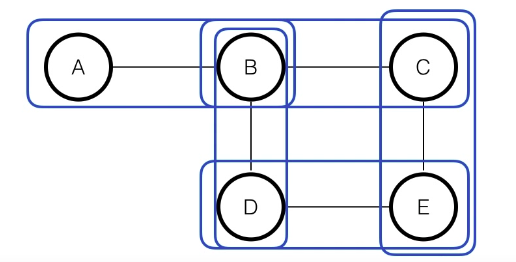
- 다음 경우도 또 다른 clique라고 볼 수 있다
-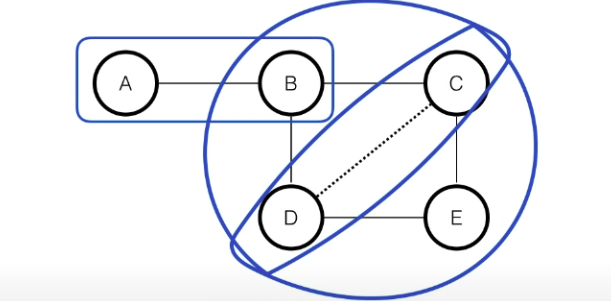
- 이 경우는, 으로 표현 가능하다.
- clique: 그래프 이론에서 그래프의 subset
-
Markov Random Fields
- 각각의 분리된 subset가 있을때, 임의의 두 subset S,T는 conditionally independent
-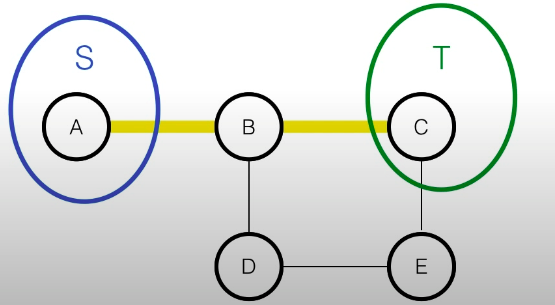
- A에서 C로 간다고 할때
- A-B-C
- A-B-D-E-C
- 위의 경로를 막는 분리된(seperating) subset을 찾으려고 할때, 세가지 경우가 있다
- 이러한 subset들이 S, T를 conditionally independent하게 한다.
- Markov Property: 인접하지 않은 경우는 conditionally independent
- Markov blanket:
- bayesian network에서의 markov blanket은 child의 parent가 markov blanket의 일부분이지만,
- Markov Random Field의 markov blanket은 단지 연결하는 부분에만 특정된다.
- bayesian network에서의 markov blanket은 child의 parent가 markov blanket의 일부분이지만,
- 각각의 분리된 subset가 있을때, 임의의 두 subset S,T는 conditionally independent
-
Markov Network와 Bayesian Network
-
-
위의 경우 처럼 edge를 pairwise한 clique로 변환하기 쉽지만,
-
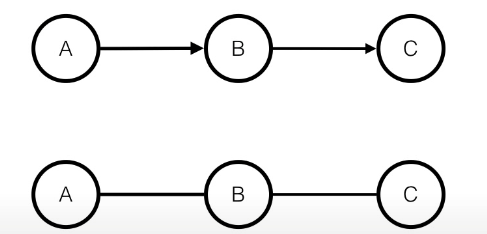
-
위와 같은 경우
- Bayesian:
- Markov:
- 위를 표현할 수 있는 많은 경우 중 하나는,
- 으로 potential function을 정할 수 있고,
- 으로 표현 할 수 있다.
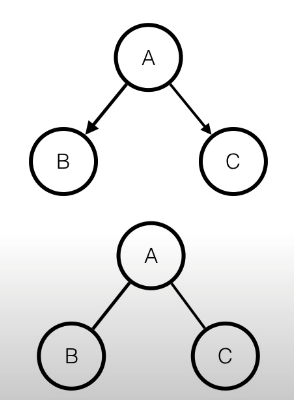
- Bayesian:
- Markov:
- 위를 표현할 수 있는 많은 경우 중 하나는,
- 으로 potential function을 정할 수 있고,
- 으로 표현 할 수 있다.
-
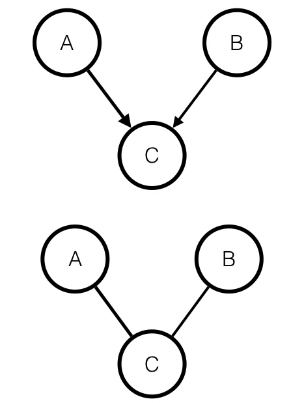
-
Bayesian:
-
Markov:
-
이전 경우같이 potential 함수를 생각해보려고 할때,
-
bayesian에서는 C가 주어졌을때 A,B는 dependent이지만,
-
markov에서는 C가 주어졌을때 A,B는 independent
-
따라서, 표현할 수 없다.
-
이를 해결하는 방법중에는 Moralizing parents라는 방법이 있다.
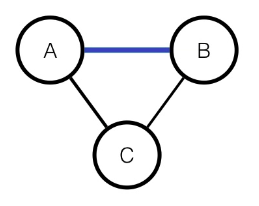
- indepent -> dependent
-