ML [8] K-means Clustering and Guassian Mixture Model (1)

본 포스팅은 카이스트 산업및시스템공학과 문일철 교수님의 Introduction to Artificial Intelligence/Machine Learning(https://aai.kaist.ac.kr/xe2/courses) 강의에 대한 학습 정리입니다.

Unsupervised Learning

: tag(label)이 없는, true value가 모르는 상황에서 패턴을 찾는 방법.

• 군집(cluster)을 찾는 방법
• latent factor를 찾는 방법
• graph structure를 찾는 방법

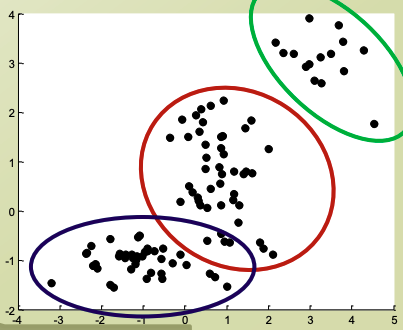
Clustering problems

• 어떻게 라벨이 없는 데이터들을 군집화할 것인가?
  • 케이스들의 기초 지식이 없음
  • class의 latent(hidden) variable이 있음
  • latent classes의 optimal assignment를 찾아야 함.

K-means Algorithm

• K-means Algorithm
• 잠재적으로 내부적인 동력이 K개가 있다고 할때, 이 동력들에 의해서 n개의 데이터가 존재하게 된다라는 가정으오 clustering하는 것.
• 일반적으로,
  • $J=\sum^N_{n=1}\sum^K_{k=1}r_{nk}||x_n-\mu_k||^2$
  • 최적화를 통한$J$를 최소화
    • $r_{nk}$: cluster할 데이터들의 assignment (0 또는 1)
    • $\mu_k$: 중심점(centroid)의 위치
  • Iterative optimization
    • $r_{nk}$와 $\mu_k$가 상호작용하기 때문.

Expectation and Maximization (EM Algorithm)

• $J=\sum^N_{n=1}\sum^K_{k=1}r_{nk}||x_n-\mu_k||^2$
  • E:
    • 주어진 파라미터에 의한 log-likelihood의 expectation
    • neareat centroid에 데이터 포인트를 assign
  • M:
    • log-likelihood관점에서 파라미터를 maximization
    • assignment가 주어진 상황에서 centroid를 update
• $r_{nk}$
  • $r_{nk} = {0,1}$
  • discrete variable
  • logical choice: $\mu_k$에 대해 데이터 $x_n$를 assignment
• $\mu_{k}$
  • $\frac{dJ}{d\mu_k}=0$
  • $\mu_k=\frac{\sum_{n=1}^Nr_{nk}x_n}{\sum_{n=1}^Nr_{nk}}$

K-Means Algorithm의 특징(problems)

• cluster의 개수는 불분명
• 중심정의 초기화를 정하는 방법
  • 어떤 초기 중심점은 적당한 결과를 줄 수 없다
• distance metric의 한계점
  • 유클리드 거리는 사전지식에 취약하다
• Hard clustering
  • 군집에 대한 데이터 포인트의 hard assignment
    • $r_{nk} = {0,1}$
      • 이 경우를 smoothing할 수 있지 않을까? => gaussian mixture model

Gaussian Mixture Model

Multinomial Distribution

• Binary varaible
  • 0또는 1
• K options의 경우
  • $K=6, X={0,0,1,0,0,0}$인 경우
  • $\sum_kx_k=1,P(x|\mu)=\prod_{k=1}^K\mu^{x_k}$
  • $\mu_k\geq0,\sum_k\mu_k=1$
  • binomial distribution의 generalization => Multinomial distribution
• dataset D를 N개의 선택을 할때,
  • $P(x|\mu)=\prod_{n=1}^N\prod_{k=1}^K\mu^{x_k}=\prod_{k=1}^K\mu_k^{\sum_{n=1}^N}=\prod_{k=1}^K\mu_k^{m_k}$
  • $\mu$의 MLE를 어떻게 결정할 것인가?
    • Maximize $P(x|\mu)=\prod_{k=1}^K\mu_k^{m_k}$
    • 조건: $\mu_k\geq0,\sum_k\mu_k=1$
    • => Lagrange Method

Lagrange Method

• 제약 조건에서 local maximum을 찾는 방법
  • maximize $f(x,y)$
  • 제약조건 $g(x,y)=c$
• 1) lagrange function 만들기
  • $L(x,y,\lambda) = f(x,y) + \lambda(g(x,y)-c)$
  • $L(\mu,m,\lambda)=\sum_{k=1}^Km_kln\mu_k+\lambda(\sum_{k=1}^K\mu_k-1)$
    • log-likelihood 이용
• 2)
  • $\frac{d}{d\mu_k}=\frac{m_k}{\mu_k}+\lambda=0\rarr\mu_k=-\frac{m_k}{\lambda}$
• 3)
  • $\sum_k\mu_k = 1 \rarr \sum_k-\frac{m_k}{\lambda}=1\rarr\sum_km_k=-\lambda\rarr\sum_k\sum_{n=1}^Nx_{nk}=-\lambda\rarr N=-\lambda$
  • $\mu_k=\frac{m_k}{N}$: multinomial distribution의 MLE 파라미터

  Mixture Model

• 세개의 서로 다른 normal distribution이 있다고 할때,
  
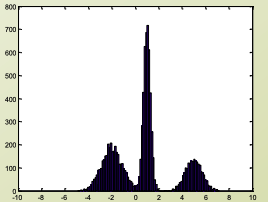
  • subpopulation이 존재
  • 전통적인 distribution은 fitting이 안되니,
  • mix해야 한다
• Mixture distribution: $P(x) = \sum_{k=1}^K\pi_kN(x|\mu_k,\sigma_k)$
  • Mixing coefficients $\pi_k$
    • 가중치 연산
    • $\sum_{k=1}^K\pi_k=1,0\leq\pi_k\leq1$
  • Mixture component$N(x|\mu_k,\sigma_k)$: subpopulation의 distribution
  • $\pi_k$를 $P(z_k)$
  • $N(x|\mu_k,\sigma_k)$를 $P(x|z)$
  • $P(x)=\sum_{k=1}^KP(z_k)P(x|z)$

Gaussian Mixture Model

• 데이터 포인트들을 mixture distribution에 있을 수 있게 하는 방법
  • $P(x)=\sum_{k=1}^KP(z_k)P(x|z)\sum_{k=1}^K\pi_kN(x|\mu_k,\sum_k)$
  • 어떻게 mixture로?
    • mixing coefficient 또는 selection variable $z_k$
      • multinomial distribution을 따르도록 selection은 stochastic하게.
    • mixture component
      • $P(X|z_k=1)=N(x|\mu_k,\sum_k)\rarr P(X|Z)=\prod_{k=1}^KN(x|\mu_k,\sum_k)^{z_k}$
  • 이것은 marginalized probability인데. conditional일때는?
    • $r(z_{nk})= P(z_k=1|x_n)=\frac{P(z_k=1)P(x|Z_k=1)}{\sum_{j=1}^KP(z_j=1)P(x|z_j=1)}=\frac{\pi_kN(x|\mu_k,\sum_k)}{\sum_{j=1}^K\pi_jN(x|\mu_j,\sum_j)}$
• 전체 데이터셋의 log-likelihood
  • $lnP(X|\pi,\mu,\sum)=\sum_{n=1}^Nln\{\sum_{k=1}^K\pi_kN(x|\mu_k,\sum_k)\}$