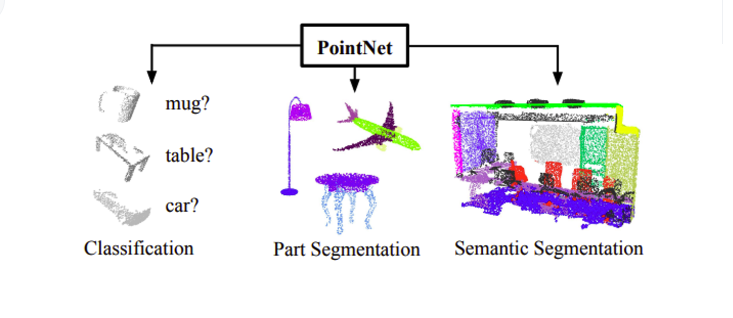
최근, Object Pop-Up 논문과 같은 point cloud를 통한 Human Object Interaction 또는 Human Pose Estimation의 연구가 많아지고 있습니다. point cloud를 통한 연구가 그동안 기술의 상용화 부족으로 주목받지 못하고 있었습니다만, 아이폰에 ToF 카메라가 사용되고 있어 Face ID에도 사용되고 있는 것을 보면, 우리 삶에 한 걸음 더 다가왔다는 것을 알 수 있습니다. 그래서 좀 더 진지하게 이를 활용하여 연구해봐야할 타이밍이 왔습니다.
point cloud를 활용하는 연구들을 살펴보면, pointNet++모델을 사용하는 경우가 굉장히 많더라구요. 그리고 PointNet++는 PointNet을 기반으로 하고 있고요. 그러니 기초부터 쌓고 가는게 맞지 않겠습니까 ㅎㅎ
오늘 리뷰할 논문은 standford 대학에서 발표한 PointNet입니다. 사실, 논문이 조오금 어렵게 표현된 부분이 있습니다만, 아이디어가 굉장히 견고한 점들과 체계적으로 설명하는 부분들이 굉장히 인상 깊었습니다.
참고로, PointNet은 2016년에 나온 논문입니다. 즉, 그 뒤로 더 많은 연구들이 있다는 겁니다 ㅎㅎ Point Cloud분야도 봐야할 것이 아주 많겠군요 ㅎㅎ
https://arxiv.org/pdf/1612.00593.pdf
https://stanford.edu/~rqi/pointnet/
https://github.com/charlesq34/pointnet
Introduction
- point cloud를 다루는 기존 Network
- input: image grid나 3D voxel과 같은 완전히 정형적인 data
- problem:
- 3D voxel grid나 image의 집합으로 변형
- 불필요한 cost
- 데이터의 모호한 invariance로 인한 quantization artifact
- point cloud란?
- 객체를 점의 집합으로 표현
- combinatorial irregularities나 mesh의 복잡성을 피할 수 있음 -> 더 학습하기 좋은 조건
- BUT, point의 집합이기 때문에
- 각 멤버를 permutations하기에 invariant (점들의 순서를 인지하기에 모호함)
- net computation에 특정 대칭화가 필요
- rigid motion의 invariance도 고려해야함
- 저자가 제안한 PointNet
- input: point cloud
- 3차원 좌표로 표현 (x,y,z)
- 그 외 추가정보는 normal계산되어 입력
- output: (task에 따라) 전체 또는 각 부분의 class labels
- 특징
- 모든 과정은 각 점에 동일하게, 독립적으로
- rigid / affine transformation을 적용하기 쉬움
- data-dependent spatial transformer network를 추가하여 데이터 정규화(canonicalize)하고 결과를 향상
- single symmetric function(max pooling) 사용
- 마지막 fc layer에 따른 task 분리 (shape classification / shape segmentation)
- input: point cloud
Problem Statement
point cloud는 각 점 가 벡터 좌표 와 필요에 따라 color, normal 등이 추가된 점의 집합 입니다. 저자들은 간단하고 명확한 실험을 위해서 추가 정보없이 좌표만 사용했다고 합니다.
Object classification에서는, network가 k개의 후보 class에 대한 k score를 반환하도록 했으며, part region segmentation에서는 n개의 점과 m개의 semantic sub-category를 output하도록 합니다.
Deep Learning on Point Sets
Properties of Point Sets in
모델의 input은 Euclidean space의, 아래 세가지의 특성을 가진 point들의 subset 입니다.
- Unordered
점들간의 순서가 없기 때문에, N개의 점들으로 이루어진 포인트 다루는 네트워크는 N에 invariant - Interaction among point
point들은 거리에 따른 공간에 위치하기 때문에, 주변 점들과 유의한 관계가 있을 것 입니다. 따라서, 모델은 주변 점들로 부터 local 구조를 파악해야하고, 이런 local 구조들간의 조합적인 작용도 인지해야합니다.
Invariance under transformations
회전이나 이동과 같은 transformation이 적용되도, 데이터의 분포 자체가 달라지는 것이 아니므로, transformation에 invariant해야 합니다.
PointNet Architecture
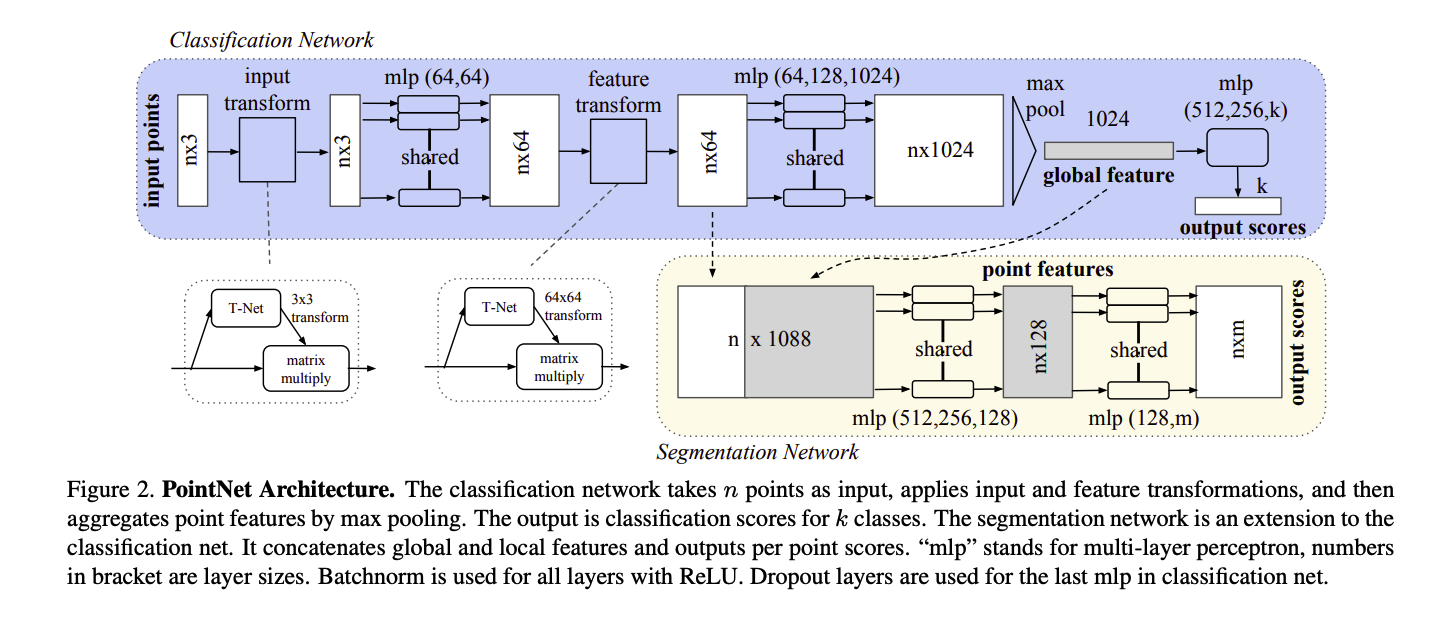
저자가 제안한 모델은 3가지의 key module로 구성됩니다.
Symmetry Function for Unordered Input
input permutation에 invariant하도록 세가지 전략을 사용합니다.
- 표준화된 순서로 input을 sorting
- RNN을 학습할때처럼 sequence를 input으로 다루지만, 다양한 조합으로 학습 데이터 augmentation
- 각 점의 정보를 aggregate하기 위한 symmetric function 사용
- 이때, symmetric function은 n개의 vector를 input으로 받고, input 순서에 invariant한 새로운 vector를 반환
sorting하는 것이 간단한 것 같지만, 고차원 space에서 point perturbation에 안정적인 순서라는 것은 없습니다. 이 부분이 모순처럼 보일 수 있습니다. 만약 ordering 전략이 있다면, 고차원 space와 1d real line간의 bijection map에 정의될 수 있는데, 그것이 고차원에서도 공간 근접성을 유지하도록 하는 것은 불가능합니다. 즉, 정렬이 포인트 변동에 대해 안정적이어야 한다는 것은 이 맵이 차원이 축소됨에 따라 공간적 근접성을 보존하도록 요구하는 것과 동등해야 합니다. 하지만 이런 경우는 달성하기 어렵기 때문에, 여전히 issue로 남아있습니다. 그래도, 저자들은 실험을 통해서, 정렬된 point set을 바로 MLP를 적용하는 것은 성능이 좋지 않지만, 정렬되지 않은 것보단 낫다는 것을 확인했습니다.
위의 순서에 관한 문제로, 저자들이 도입한 것은 순서에 invariant한 RNN방식입니다. 안타깝게도, RNN도 element가 point cloud처럼 많은 경우에는 성능이 좋지 못했습니다. 그래서 제안한 일반 함수를 근사하는 방법은 symmetric sunction을 transformed 요소에 적용하는 것입니다.
저자가 제안한 방법은 간단합니다. multi-laywer perceptron network로 h를, variable function과 max pooling으로 g를 근사합니다. 이렇게 만들어진 h를 모아, 세트의 각각 다른 특성들을 합쳐 여러개의 f를 만듭니다.
⭐️⭐️⭐️좀 더 쉽게 설명해보겠습니다.⭐️⭐️⭐️
개인적으로, 저는 위의 부분에 대해서 조금 어렵게 설명했다라고 생각합니다. 그래서 제가 조금 더 쉽게 설명해보려고 합니다.
우선, point cloud는 점의 집합이라는 것을 알고 있죠. 보통, 우리가 이러한 point들을 하나의 sequence로 모아서 모델에 입력할 때, 어떤 점을 먼저 처음으로 잡고, 다른 점들을 어떤 순서로 배치할지에 대해 정해야하죠. 근데 point cloud에서 그게 가능한가요? 조금 애매하죠? 왜냐하면, 그 순서를 잡는 방법이 어떻든 같은 output을 가져야 하니까요. 그래서, 저자 제안한 방법이 "symmetric function(대칭 함수)을 도입하자"입니다.
symmetric funtion이라는 것은 input 집합을 어떤 순서로 넣어도 같은 output이 나오도록 하는 함수입니다. 가장 쉬운 예를 들자면, 와 입니다. 이니까요.
대칭 함수가 이해되었다면, 저자가 설계하고자하는 모델로 대칭함수를 가져오는 겁니다.
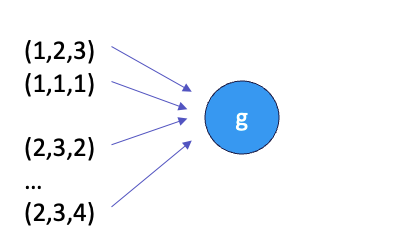
위와 같은 input들에 상관없이 같은 output을 줄 수 있는 symmetric function g를 놓습니다. 그리고 여기서 g를 max함수라고 하면, 아웃풋은 (2,3,4)겠죠. 근데, 너무 단순하지 않나요? input이 적으면 모르겠는데, point가 엄청 많은 cloud라면, input의 정보를 너무 조금만 쓰는 것이 아쉽습니다.
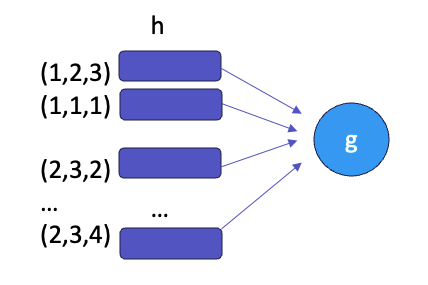
그래서, 저자들이 도입한 방법은 g함수에 입력하기 전에, input을 고차원은 만들어 주는 것입니다. 그럼, input을 더 잘 활용할 수 있겠죠. 하지만, 저자는 이에 그치지 않습니다.
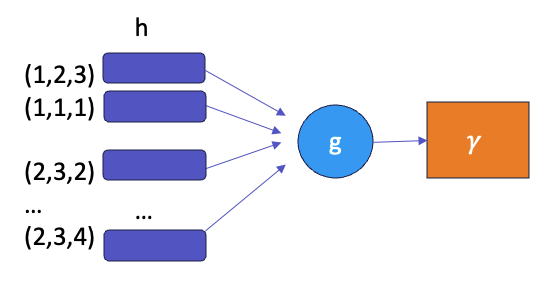
더 많은 feature를 extraction하기 위해서, 함수 g 이후에, γ를 추가하죠.
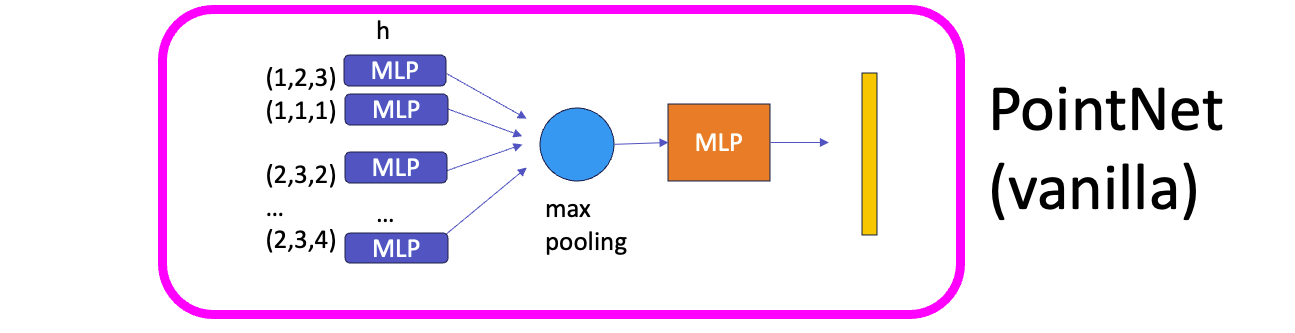
마지막으로, 함수g, input을 고차원으로 만드는 방법과, 함수 gamma를 정합니다. 저자들은 실험적으로 각각, max pooling, MLP와 MLP로 이를 결정하여, 가장 vanilla한 pointNet을 정의합니다.
Local and Global Information Aggregation
위에서 생성된 벡터 는 input set의 global signiture입니다. 그럼 여기서 SVM이나 MLP classifier를 통하여 classification할 수 있습니다. 하지만, point segmentation을 위해선 local 정보도 필요하죠.
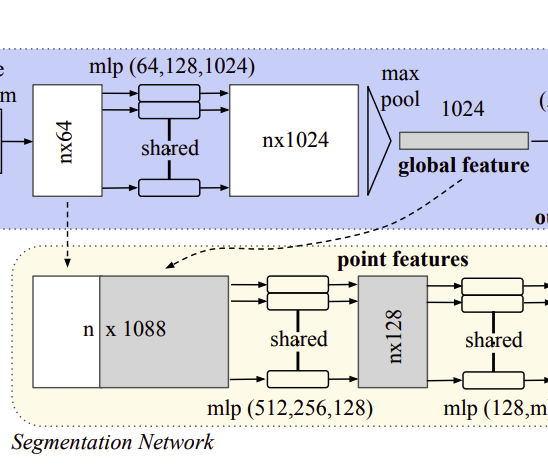
Fig 2.에서 보이는 것 처럼, segmentation을 위해서 local feature와 global feature를 concat하여 n×1088의 새로운 벡터를 만들고, 다시 FC layer를 저쳐 새로운 벡터를 만듭니다.
Joint Alignment Network
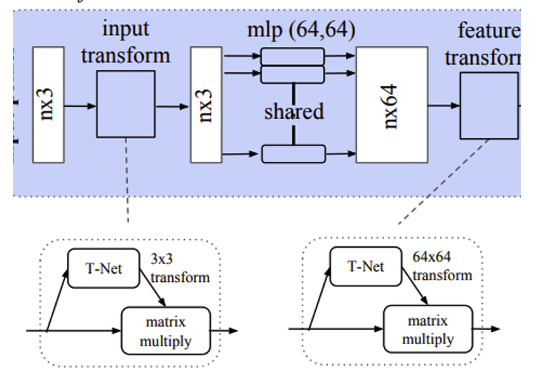
Introduction에서 계속 강조한 것 처럼, semantic labeling은 어떤 transformation에도 invariant, 즉, 불변해야합니다. 기존 연구들은 이 문제를 feature extraction전에 표준화된 공간에 input set를 넣는 방법으로 해결하여했습니다. 하지만 저자는 더 간단하게, T-Net을 통해서 affine transformation matrix를 추정하고, input 좌표에 이러한 transformation을 적용하도록 했습니다.
이러한 아이디어는 feature space를 정렬하는 방법으로도 확장 될 수 있습니다. 하지만 또다른 네크워크를 추가하면 transformation matrix의차원이 spatial transform matrix보다 커져 optimization이 어려워질 수 있기 때문에, 저자는 softmax 학습 loss에 regularization 공식을 추가했습니다.
Experiment
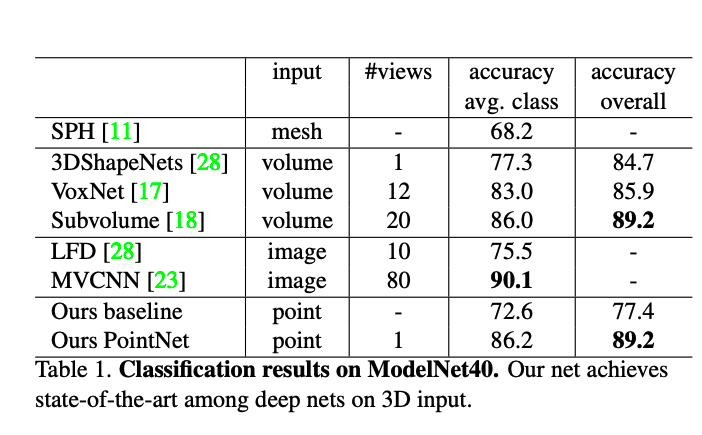
위의 Table1을 보시면 classification 부분에서의 pointNet이 기존 모델들 보다 좋은 성능을 보이거나 비슷한 것을 알 수 있습니다.
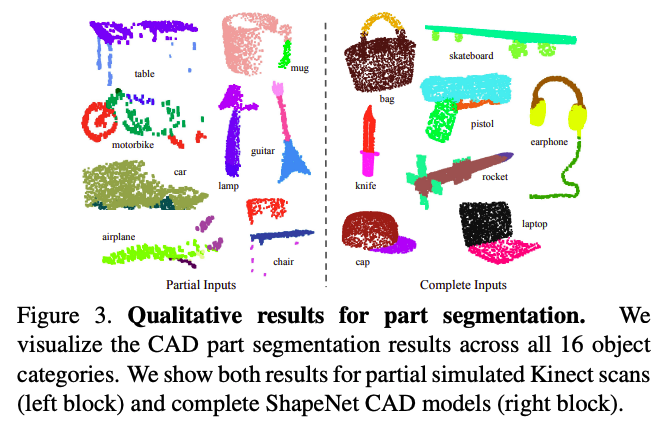
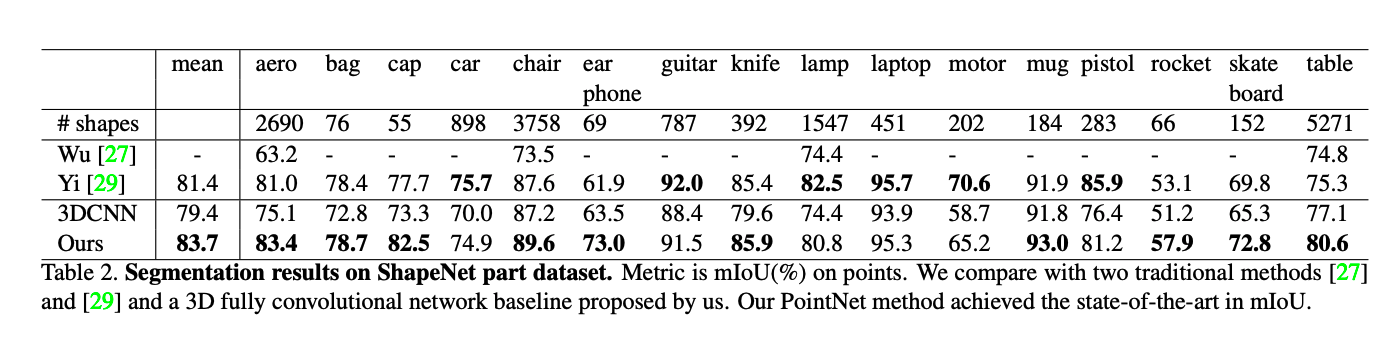

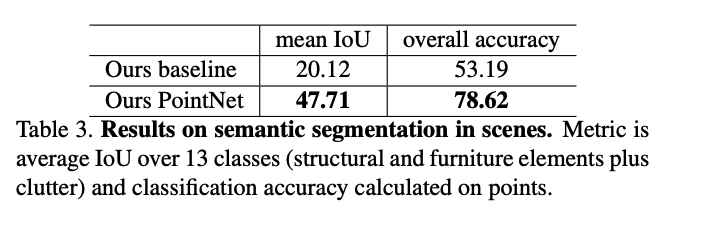
위의 Figure 3,4과 Table2을 보시면 segmentation 부분에서의 pointNet이 기존 모델들 보다 좋은 성능을 보이거나 비슷한 것을 알 수 있습니다.
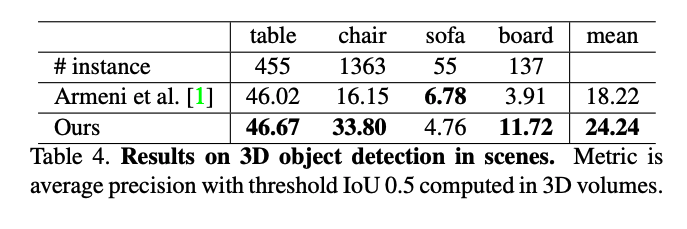
segmenation 이외에도, 3D object detection에서도 좋은 성능을 보이죠.
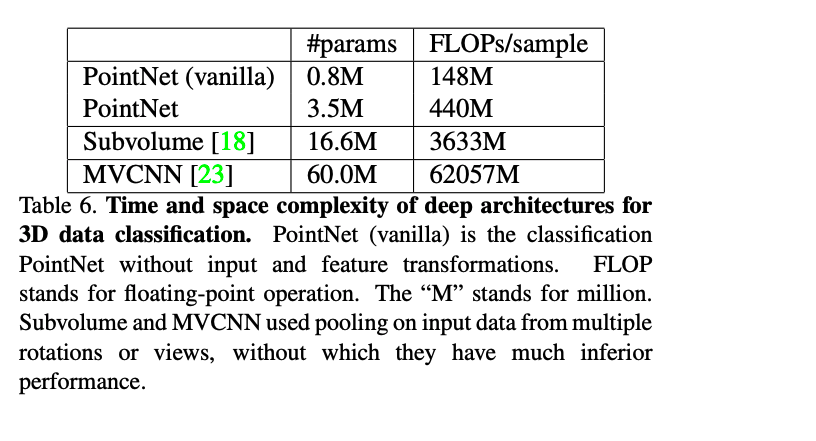
또한, 다른 모델들과 비교해봤을때, 가벼운 모델입니다.

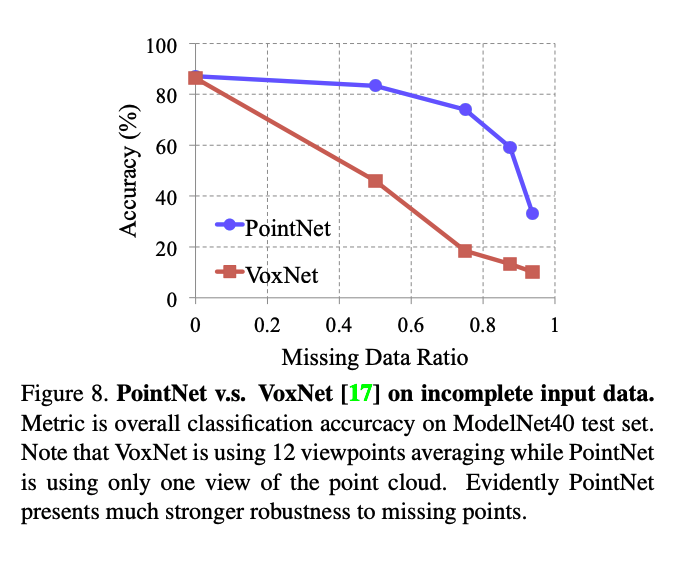
위 실험은 점들이 부족할때, 얼마나 강인한 성능을 갖고 있는지에 대한 결과입니다. pointNet은 점이 좀 부족하더라도, 비교적 일정한 결과를 보여줍니다.
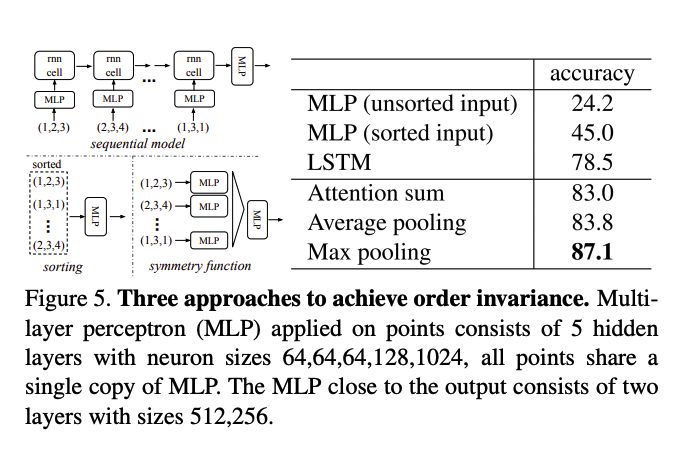

마지막으로, 도입한 방법들에 대한 실험 결과를 보여주며, 제안한 방법의 타당성을 증명합니다.

명쾌한 논문 리뷰 감사합니다!
근데 논문의 supplementary 부분을 봐도 T-NET에 대해서는 자세하게 안나오는 것 같은데 혹시 T-NET에 대한 추가적인 설명 부탁드려도 될까요??