[논문] PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space

지난 PointNet에 이어, 그의 확장판인 PointNet++도 리뷰해봤습니다.
제가 최근에 본 논문들에서 pointNet++을 많이 사용하던데, 생각보다 적은 수의 point를 이용하여 결과를 취득했는데, 그 부분이 조금 의아했습니다. point가 생각보다 몇개없는데?(256 ~ 512개)도 이게 맞나? 싶었는데, 그 부분을 논문을 읽어보니 납득이 되었고, 실제 실험까지도 해보셨더라구요. 역시 똑똑한 사람들....
그리고 논문도 PointNet보다도 좀 더 읽기 편합니다. 왜냐면 이전 PointNet은 너무 어려워 보이게 쓰셨더라구요. 아마 읽어보시고 이해과정을 다 마치신 분들은 인정하실겁니다....하하...😅 여튼, PointNet을 읽고, pointNet++을 보면, 아주 수월하게 이해되실거라 생각합니다 ㅎㅎ

https://arxiv.org/abs/1706.02413
https://github.com/charlesq34/pointnet2
https://stanford.edu/~rqi/pointnet2/

Introduction

저자는 이전 연구인 PointNet과 CNN을 비교하며, PointNet의 아쉬운 점을 지적합니다.

• pointNet
  • 각 point의 spatial encoding하고 통합하여 global한 feature를 추출
  • metric에 의한 local 구조 파악 불가능
• CNN
  -input을 grid에 정의하여 multi-resolution 계층에 따른 점진적 scale 증가에 맞는 feature 추출가능

PointNet++은 pointNet에 CNN이 가진 점진적 구조를 더하고자 했습니다. 우선 point세트를 거리에 다라 서로 겹치는 local 영역으로 나눕이다. 그리고, CNN처럼, 작은 이웃들에서 local feature를 뽑아냅니다. 마지막으로 이러한 local feature들을 더 큰 집합으로 만들어 더 높은 차원에서 feature를 뽑아냅니다. 이 과정을 모든 point set의 feature를 얻을 때까지 반복합니다.

위 과정에서 또 짚고 넘어가야할 것이 있는데, 어떻게 point set를 나눌지와 local feature learner를 통한 local feature와 point set를 추출을 어떻게 할 것인지 입니다. point set를 나누는 것은 나눠진 부분들이 공통적인 구조를 만들어야하고, 그에 따라 local feature learner가 같은 convolutional setting을 통해 공유될 수 있기 때문에, 이 두 문제는 서로 연관되어 있습니다. 여기서 말하는 local feauture learner는 PointNet입니다.

이 외에도, 어떻게 point set의 겹쳐지는 부분을 만들어 낼 것인지도 생각해봐야 합니다. 각 부분은 Euclidean 공간에 있는 중심과 반지름이 있는 이웃 구(球)를 의미합니다. 전체 set를 고르게 고르기 위해서는 farthest point sampling(FPS) 알고리즘을 사용합니다. 정해진 stride를 가진 CNN과 비교해보면, pointNet++의 local receptice field는 input data와 그 거리를 어떻게 정할지에 대한 metric에 따라 다르기 때문에, 효율적이고 효과적입니다. 다만, input point cloud의 density에 따라서, 하나의 구 안에 포함되는 point의 수도 달라집니다. 따라서, 이 부분은 실험적으로 구의 크기를 정해야하는 점이 있습니다.

Problem Statement

$X=(M,d)$를 Euclidean space $R^n$에 속하는 discrete metric space, $M\subseteq R^n$은 point set, $d$는 distance metric이라고 하고, ambient euclidean space(환경 공간)상의 $M$의 density는 정형화되어 있지 않습니다. 저자는 $X$를 input으로 받는 learning set function $f$를 사용하여 $X$에 따른 정보를 만들어 내도록 합니다.

Method

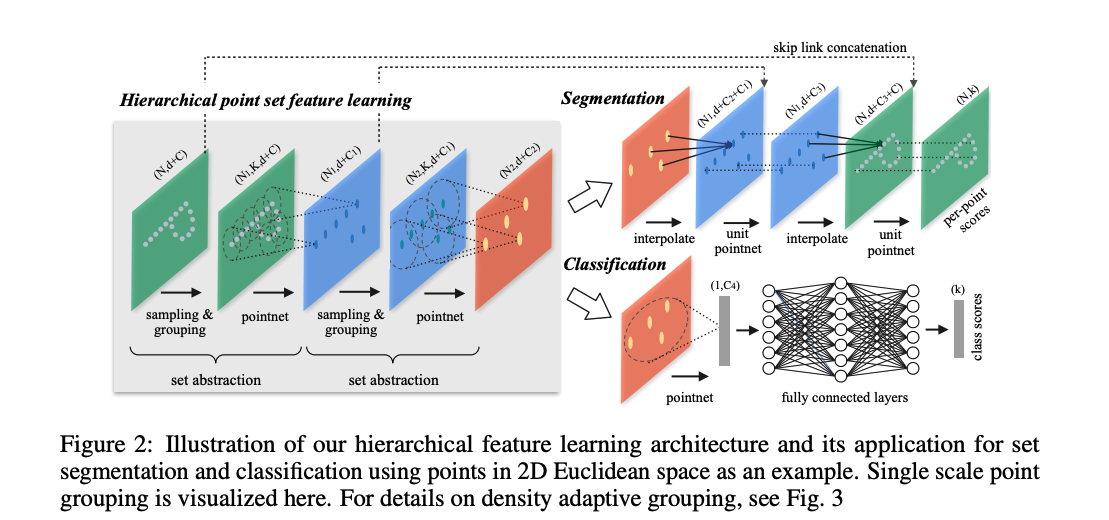
Hierarchical Point Set Feature Learning

Fig 2의 set abstraction 부분은 작은 요소들의 특징을 추출하는데, sampling layer, grouping layer pointNet layer로 이루어져있습니다. 이 부분은 $d$차원 좌표와 $C$차원 point feature의 $N$개의 point들로 이루어진 $N\times(d+C)$ Matrix를 input으로 받아, $d$차원 좌표와 local context를 함축하는 $C'$차원 feature vector의 $N'$개의 subsample point의 $N'\times (d+C')$ Matrix를 output으로 합니다.

Sampling layer

주어진 input point $\{x_1,x_2, ..., x_n\}$에, farthest point sampling (FPS) 알고리즘을 사용하여, point들의 subset $\{x_{i_1},x_{i_2}, ...,x_{i_m}\}$를 골라냅니다. 이때, $x_{i_j}$는 $\{x_{i_1},x_{i_2}, ...,x_{i_{j-1}}\}$에서 가장 멀리 있는 점 입니다. random sampling과 비교했을때, 같은 중심점 개수를 가진 상황에서 전체 point set를 잘 포함 시켰다고 합니다. CNN과 비교했을때도, 이러한 sampling 방법은 데이터에 의존적인 방식으로 receptive field를 만들었습니다.

Grouping layer

이 layer에서는 $N\times(d+C)$의 point set와 $N'\times d$사이즈의 중심점 한 세트를 입력으로 받아, $K$개의 중심점 neighborhood에 있는 점들로 이루어진 $N'\times K \times (d+C)$사이즈의 point set 그룹을 output합니다. 여기서, $K$는 group마다 다르겠지만, point layer를 거치면서 고정된 크기의 local region feature vector로 변환될 수 있습니다.

CNN은 하나의 픽셀로 부터 특정 Mehattan distance (=kernel size) 만큼의 위치한 픽셀들까지 포함하여 local region을 정의하지만, pointNet++에서는 이웃한 metric 거리에 있는 metric space로 정의합니다.

저자는 이런 neighborhood를 정의하는데 KNN 알고리즘을 사용하지 않고 구(ball)를 사용했는데, 그 이유는 고정된 region scale을 보장하여 local region feature를 공간상에서 더 general하게 할 수 있기 때문입니다.

PointNet layer.

PointNet Layer에서는 $N'$개의 local region을 input으로 받아, $N'\times(d+C')$ 개의 각 local region을 output합니다.
하나의 local region의 point 좌표는 먼저 centroid point(중심점)과 연관된 local frame으로 변환되고, pointNet을 통해 local pattern을 학습합니다.

Robust Feature Learning under Non-Uniform Sampling Density

point cloud 데이터는 지역마다 점의 밀도가 다 다릅니다. 그래서 밀도가 높은 곳에서는 sparse하게 sampling될때 generalize가 안되고, 반대로, 밀도가 낮은 곳에서는 전체적인 local structure를 알기 어렵죠.
그래서 저자는 밀집된 영역에서는 가능한 세밀하게 디테일을 파악할 수 있도록 하려 했습니다. 하지만, 이런 방법은 점들이 부족하게 취득되어 밀도가 낮은 곳에 적용하면 안되기 때문에, 더 큰 근접 영역에 맞는 더 큰 scale pattern이 필요했습니다. 최종적으로, 저자가 제안한 것은 밀도에 따라서 feature를 합치는 방법을 제안합니다.

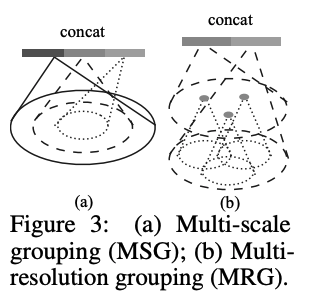
Multi-scale grouping (MSG).

MSG는, Fig 3 (a)처럼, 각각 다른 크기를 가진 그룹의 feature를 합치는 방법입니다.
또한, network를 학습할 때, 최적화를 위해 random input dropout을 도입하는데, 이름처럼 point를 일정 확률로 랜덤하게 빼고 학습하는 방법입니다. 저자는 이때 확률 $\theta$를 0.95로 설정합니다.

Multi-resolution grouping (MRG).

MSG방식은 모든 중심점의 큰 neighborhood에서 local PointNet을 동작하는 방법으로, 계산량이 많습니다. 특히 앞 단계일 수록 계산량이 크겠죠. 그래서 새로 제안한 방법인 MRG는 계산량은 적지만 점들의 분포 특징에 따라 정보를 적절히 합할 수 있는 방법입니다. 이 방법은, Fig 3(b)에서 보이는 바와 같이, 특정 단계 $L_i$일때 두 개의 벡터를 합하는 방식입니다. 이 두 벡터는 좀 더 낮은 레벨$L_{i-1}$에서 가져오는 feature와 해단 구역에서 바로 뽑아오는 feature입니다.
추가로, 이 두 벡터는 상황에 따라 weight를 달리하여 concat되는데, 밀도가 낮을때는 두 번째 벡터에 높은 weight를, 밀도가 높을때는 첫번째 벡터에 높은 weight를 줍니다.

Point Feature Propagation for Set Segmentation

앞서 설명된 부분들은 classification을 위해서 원래 점들이 subsample된 것으로 볼 수 있는데, segmentation의 경우는 다시 원상 복구해서 원래 점들 하나하나의 label을 파악해야합니다. 가장 단순하게 모든 set abstraction level에서 모든 점들을 중심점으로 샘플링하는 것인데, 계산량이 매우 커지죠. 그래서, 저자들은 subsampling된 점들을 원래 점들로 feature를 propagate하는 방법을 채택합니다.
저자는, Fig 2의 오른쪽 상단처럼, 거리 기반의 interpolation과 level skip link를 통해서 계층적 propagation 방법을 사용합니다. feature propagation 단계에서는, $N_{l-1}$과 $N_l$이 각각 set abstraction level $l$의 input과 output의 point set size인 곳에서, $N_l\times (d+C)$의 점들을 $N_{l-1}$points로 point feature를 propagate합니다. 이 feature propation은 $N_{l-1}$개의 점들의 과표에서 $N_l$점들의 feature vlaue $f$를 interpolation하여 얻습니다. 더 구체적으로, 여기서 사용하는 interpolation은 KNN기반으로 하되, 거리와는 반대로 weight를 가지는 방법입니다. KNN의 방식은 아래와 같으며, 저자는 $p=2,k=3$을 채택사용했습니다.

• $f^{(j)}(x)=\frac{\sum^k_{i=1}w_i(x)f^{(j)}_i}{\sum^k_{i=1}w_i(x)}$
  • $w_i(x)=\frac{1}{d(x,x_i)^p},j=1, ...,C$

위에서 $N_{l-1}$에서 interplate된 feature는 skip link하여 가져온 set abstraction 에서의 feature를 concat하고, (CNN에서 $1\times 1$conv과 같은) "unit PointNet"에 넣습니다. 그리고, 마지막에 fully connected와 ReLU를 적용하여 각 점의 feature vector를 업데이트하고, 이 과정을 원래 점들이 다 원상복귀될때까지 수행합니다.

Experiments

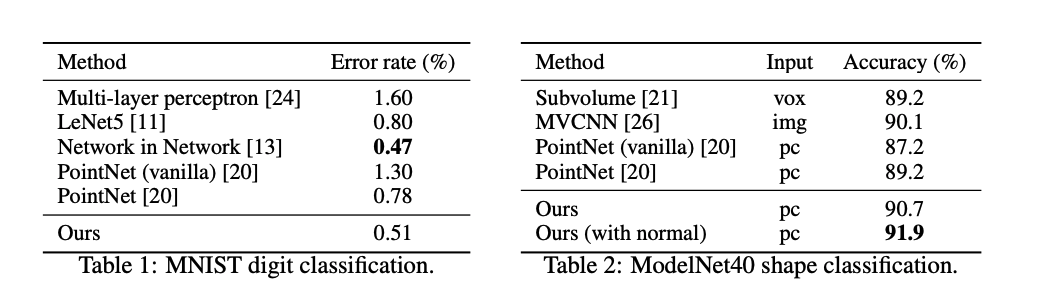
위의 그림과 같이, classification에서는, 이전 PointNet이 넘지 못한 MVCNN의 성능을 넘었을 정도의 성능을 보였습니다.

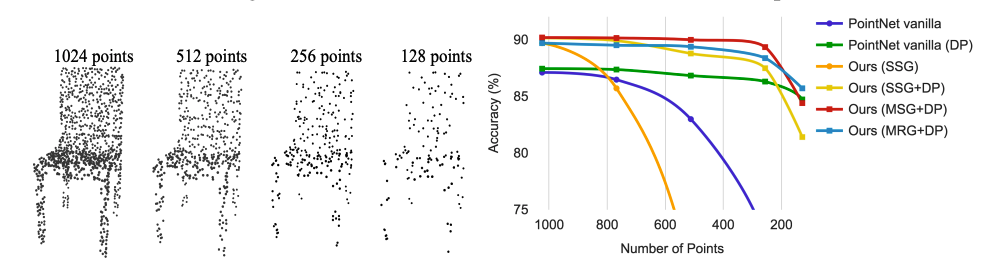
위 실험은 저자들이 제안한 방법들을 사용했을때, 취득된 point cloud의 점 개수에 따른 성능변화를 보여줍니다. 이로써, 저자가 제안한 방법을 사용하면, 점이 굳이 많이 없어도 좋은 성능을 보여줌을 알 수 있습니다.

segmenation의 성능입니다.

각 metric space에 대한 성능 입니다.