Regression exercise (Linear, Logistic, Negative Binomial or Poisson)

Jihwan Oh·2023년 12월 14일
Regressionlinearlogisticnegative binomialpoisson
0

data analysis

목록 보기
9/9
#############################################
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
#############################################

문제1. Linear Regression (총 30점)

a. 주어진 데이터를 데이터프레임화 하기 (DataFrame) (5점)
b. 데이터를 바탕으로 선형회귀식을 구하시오. (5점) 이때, CRIM, NDUS, NOX, AGE, PTRATIO 를 독립변수로 활용하시오.
c. 유의수준 0.05에서 유의미하다고 판단되는 독립변수를 찾고, 해당 변수의 회귀계수의 의미를 해석하시오. (10점)
d. 결과들을 바탕으로 결정계수를 구하고 그 의미를 종속변수의 총변동(SST)를 활용하여 설명할 것. (10점)

보스턴 주택가격 데이터

종속변수

  • PRICE: 본인 소유의 주택 가격 (단위: 달러)

독립변수

  • CRIM: 지역별 범죄 발생률 (단위: %)
  • ZN: 25,000평방피트를 초과하는 거주 지역의 비율
  • NDUS: 비상업 지역 넓이 비율 (단위: %)
  • CHAS: 찰스강에 대한 더미 변수(강의 경계에 위치한 경우는 1, 아니면 0)
  • NOX: 일산화질소 농도 (단위: ppm)
  • RM: 거주할 수 있는 방 개수
  • AGE: 1940년 이전에 건축된 소유 주택의 비율 (단위: %)
  • DIS: 5개 주요 고용센터까지의 가중 거리
  • RAD: 고속도로 접근 용이도
  • TAX: 10,000달러당 재산세율
  • PTRATIO: 지역의 교사대비 학생 수 비율 (단위: %)
  • LSTAT: 하위 계층의 비율
#######이 셀을 실행하면 데이터가 받아집니다. 실행만 하고 이 셀을 변형시키려 하지 마세요.###########
import pandas as pd
import numpy as np
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
data = np.delete(data, 11, axis = 1) #독립변수 데이터
target = raw_df.values[1::2, 2] #종속변수 데이터
print('data: ', data)
print('target: ', target)
data:  [[6.3200e-03 1.8000e+01 2.3100e+00 ... 2.9600e+02 1.5300e+01 4.9800e+00]
 [2.7310e-02 0.0000e+00 7.0700e+00 ... 2.4200e+02 1.7800e+01 9.1400e+00]
 [2.7290e-02 0.0000e+00 7.0700e+00 ... 2.4200e+02 1.7800e+01 4.0300e+00]
 ...
 [6.0760e-02 0.0000e+00 1.1930e+01 ... 2.7300e+02 2.1000e+01 5.6400e+00]
 [1.0959e-01 0.0000e+00 1.1930e+01 ... 2.7300e+02 2.1000e+01 6.4800e+00]
 [4.7410e-02 0.0000e+00 1.1930e+01 ... 2.7300e+02 2.1000e+01 7.8800e+00]]
target:  [24.  21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 15.  18.9 21.7 20.4
 18.2 19.9 23.1 17.5 20.2 18.2 13.6 19.6 15.2 14.5 15.6 13.9 16.6 14.8
 18.4 21.  12.7 14.5 13.2 13.1 13.5 18.9 20.  21.  24.7 30.8 34.9 26.6
 25.3 24.7 21.2 19.3 20.  16.6 14.4 19.4 19.7 20.5 25.  23.4 18.9 35.4
 24.7 31.6 23.3 19.6 18.7 16.  22.2 25.  33.  23.5 19.4 22.  17.4 20.9
 24.2 21.7 22.8 23.4 24.1 21.4 20.  20.8 21.2 20.3 28.  23.9 24.8 22.9
 23.9 26.6 22.5 22.2 23.6 28.7 22.6 22.  22.9 25.  20.6 28.4 21.4 38.7
 43.8 33.2 27.5 26.5 18.6 19.3 20.1 19.5 19.5 20.4 19.8 19.4 21.7 22.8
 18.8 18.7 18.5 18.3 21.2 19.2 20.4 19.3 22.  20.3 20.5 17.3 18.8 21.4
 15.7 16.2 18.  14.3 19.2 19.6 23.  18.4 15.6 18.1 17.4 17.1 13.3 17.8
 14.  14.4 13.4 15.6 11.8 13.8 15.6 14.6 17.8 15.4 21.5 19.6 15.3 19.4
 17.  15.6 13.1 41.3 24.3 23.3 27.  50.  50.  50.  22.7 25.  50.  23.8
 23.8 22.3 17.4 19.1 23.1 23.6 22.6 29.4 23.2 24.6 29.9 37.2 39.8 36.2
 37.9 32.5 26.4 29.6 50.  32.  29.8 34.9 37.  30.5 36.4 31.1 29.1 50.
 33.3 30.3 34.6 34.9 32.9 24.1 42.3 48.5 50.  22.6 24.4 22.5 24.4 20.
 21.7 19.3 22.4 28.1 23.7 25.  23.3 28.7 21.5 23.  26.7 21.7 27.5 30.1
 44.8 50.  37.6 31.6 46.7 31.5 24.3 31.7 41.7 48.3 29.  24.  25.1 31.5
 23.7 23.3 22.  20.1 22.2 23.7 17.6 18.5 24.3 20.5 24.5 26.2 24.4 24.8
 29.6 42.8 21.9 20.9 44.  50.  36.  30.1 33.8 43.1 48.8 31.  36.5 22.8
 30.7 50.  43.5 20.7 21.1 25.2 24.4 35.2 32.4 32.  33.2 33.1 29.1 35.1
 45.4 35.4 46.  50.  32.2 22.  20.1 23.2 22.3 24.8 28.5 37.3 27.9 23.9
 21.7 28.6 27.1 20.3 22.5 29.  24.8 22.  26.4 33.1 36.1 28.4 33.4 28.2
 22.8 20.3 16.1 22.1 19.4 21.6 23.8 16.2 17.8 19.8 23.1 21.  23.8 23.1
 20.4 18.5 25.  24.6 23.  22.2 19.3 22.6 19.8 17.1 19.4 22.2 20.7 21.1
 19.5 18.5 20.6 19.  18.7 32.7 16.5 23.9 31.2 17.5 17.2 23.1 24.5 26.6
 22.9 24.1 18.6 30.1 18.2 20.6 17.8 21.7 22.7 22.6 25.  19.9 20.8 16.8
 21.9 27.5 21.9 23.1 50.  50.  50.  50.  50.  13.8 13.8 15.  13.9 13.3
 13.1 10.2 10.4 10.9 11.3 12.3  8.8  7.2 10.5  7.4 10.2 11.5 15.1 23.2
  9.7 13.8 12.7 13.1 12.5  8.5  5.   6.3  5.6  7.2 12.1  8.3  8.5  5.
 11.9 27.9 17.2 27.5 15.  17.2 17.9 16.3  7.   7.2  7.5 10.4  8.8  8.4
 16.7 14.2 20.8 13.4 11.7  8.3 10.2 10.9 11.   9.5 14.5 14.1 16.1 14.3
 11.7 13.4  9.6  8.7  8.4 12.8 10.5 17.1 18.4 15.4 10.8 11.8 14.9 12.6
 14.1 13.  13.4 15.2 16.1 17.8 14.9 14.1 12.7 13.5 14.9 20.  16.4 17.7
 19.5 20.2 21.4 19.9 19.  19.1 19.1 20.1 19.9 19.6 23.2 29.8 13.8 13.3
 16.7 12.  14.6 21.4 23.  23.7 25.  21.8 20.6 21.2 19.1 20.6 15.2  7.
  8.1 13.6 20.1 21.8 24.5 23.1 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9
 22.  11.9]

a. 주어진 데이터를 테이터프레임화 하기. (5점)

# data 변수는 아래 컬럼명 순서대로 열이 배치되어 있음.

columns_name = ['CRIM', 'ZN', 'NDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'LSTAT']
# data = 독립변수 데이터
# target = 종속변수 데이터
#############################################
X_df = pd.DataFrame(data = data, columns = columns_name)
X_df = X_df[['CRIM', 'NDUS', 'NOX', 'AGE', 'PTRATIO']]
y_df = pd.DataFrame(data = target, columns = ['price'])
df = pd.concat([X_df, y_df], axis = 1)
df
#############################################
CRIM NDUS NOX AGE PTRATIO price
0 0.00632 2.31 0.538 65.2 15.3 24.0
1 0.02731 7.07 0.469 78.9 17.8 21.6
2 0.02729 7.07 0.469 61.1 17.8 34.7
3 0.03237 2.18 0.458 45.8 18.7 33.4
4 0.06905 2.18 0.458 54.2 18.7 36.2
... ... ... ... ... ... ...
501 0.06263 11.93 0.573 69.1 21.0 22.4
502 0.04527 11.93 0.573 76.7 21.0 20.6
503 0.06076 11.93 0.573 91.0 21.0 23.9
504 0.10959 11.93 0.573 89.3 21.0 22.0
505 0.04741 11.93 0.573 80.8 21.0 11.9

506 rows × 6 columns

<svg xmlns="http://www.w3.org/2000/svg" height="24px"viewBox="0 0 24 24"
width="24px">



b. 데이터를 바탕으로 선형회귀식을 구하시오. (5점)

  • 이때, 독립변수: CRIM, NDUS, NOX, AGE, PTRATIO /종속변수: PRICE
#############################################
model = smf.ols('price ~ CRIM + NDUS + NOX + AGE + PTRATIO', data = df).fit()
model.summary()
#############################################
OLS Regression Results
Dep. Variable: price R-squared: 0.395
Model: OLS Adj. R-squared: 0.389
Method: Least Squares F-statistic: 65.27
Date: Sun, 18 Jun 2023 Prob (F-statistic): 2.12e-52
Time: 12:45:42 Log-Likelihood: -1713.1
No. Observations: 506 AIC: 3438.
Df Residuals: 500 BIC: 3464.
Df Model: 5
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 63.3828 3.816 16.608 0.000 55.885 70.881
CRIM -0.1527 0.042 -3.609 0.000 -0.236 -0.070
NDUS -0.1757 0.079 -2.228 0.026 -0.331 -0.021
NOX -15.5243 5.086 -3.052 0.002 -25.517 -5.532
AGE 5.59e-05 0.017 0.003 0.997 -0.034 0.034
PTRATIO -1.6111 0.167 -9.655 0.000 -1.939 -1.283
Omnibus: 195.283 Durbin-Watson: 0.849
Prob(Omnibus): 0.000 Jarque-Bera (JB): 744.372
Skew: 1.755 Prob(JB): 2.30e-162
Kurtosis: 7.794 Cond. No. 1.41e+03


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.41e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

정답

a. y^=63.3828−0.1527xCRIM−0.1757xNDUS−15.5243xNOX+5.59×10−5xAGE−1.6111xPTRATIO\hat{y} = 63.3828 - 0.1527x_{CRIM} - 0.1757x_{NDUS} - 15.5243x_{NOX} + 5.59\times 10^{-5}x_{AGE} - 1.6111x_{PTRATIO}

b. CRIM, NDUS, NOX, PTRATIO

  • CRIM: 지역별 범죄 발생율이 1% 증가하면 주택가격은 0.1527 달러 감소한다.
  • NDUS: 비상업지역 넓이 비율이 1% 증가하면 주택가격은 0.1757 달러 감소한다.
  • NOX: 일산화질소 농도가 1ppm 증가하면 주택가격은 15.5243 달러 감소한다.
  • PTRATIO: 지역의 교사대비 학생수 비율이 1% 증가하면 주택가격은 1.6111 달러 감소한다.

c. 0.395, 결정계수는 총변동(SST)에서 회귀제곱값 SSR이 차지하는 비율이다. 즉, y의 총변동중 선형회귀모형에 의하여 39.5%만큼 설명될 수 있다.

문제2. Logistic Regression (총 30점)

a. 주어진 데이터를 데이터프레임화 하기 (DataFrame) (10점)
b. 데이터를 바탕으로 로지스틱 회귀식을 구하시오. (5점) 이때, 독립변수는 mean radius 만 사용할 것.
c. 실제 데이터와 로지스틱 회귀식을 한 그림에 겹쳐서 그릴 것. (5점)
d. 독립변수의 회귀계수의 의미를 로짓변환의 관점에서 해석할 것. (5점)
e. 독립변수의 승산비율을 구하고 의미를 해석할 것. (5점)

유방암 진단 데이터

종속변수

  • cancer : 암에 걸리면 0, 아니면 1

독립변수 (사진으로 찍은 종양의 특징들)

  • mean_radius: 종양의 반지름 (단위: mm)
  • mean_texture: 종양 질감
  • mean_perimeter: 종양 둘레
  • mean_area: 종양 면적
  • mean_smoothness: 종양 매끄러움 정도
  • mean_compactness: 종양의 조그만 정도
  • mean_concavity: 종양의 오목함 정도
  • mean_concave points: 종양의 오목한 점의 수
  • mean_symmetry: 종양의 대칭 정도
  • mean_fractal dimension: 종양의 프랙탈 차원
#######이 셀을 실행하면 데이터가 받아집니다. 실행만 하고 이 셀을 변형시키려 하지 마세요.###########
import pandas as pd
import numpy as np
from sklearn.datasets import load_breast_cancer

breast_cancer = load_breast_cancer()
data = breast_cancer.data[:, :10] #독립변수
target = breast_cancer.target #종속변수
print(data.shape)
print(target.shape)
(569, 10)
(569,)
# data 변수는 아래 컬럼명 순서대로 열이 배치되어 있음.
columns_name = breast_cancer.feature_names[:10]
print(columns_name)
['mean radius' 'mean texture' 'mean perimeter' 'mean area'
 'mean smoothness' 'mean compactness' 'mean concavity'
 'mean concave points' 'mean symmetry' 'mean fractal dimension']

a. 주어진 데이터를 테이터프레임화 하기. (10점)

  • 이때, 종속변수가 0과 1로 구성되어 있는데, 0이었던 값은 1로, 1이었던 값은 0으로 바꿔서 데이터프레임화할 것. (양성이 0, 음성이 1 이었던 것을 음성이 0, 양성이 1이 되도록)

  • 컬럼명 사이에 띄어쓰기가 되어 있는데 (ex, mean radius) 띄어쓰기를 없애고 underbar 로 대체할 것. (ex, mean_radius)

#############################################
columns_name = [col.replace(' ', '_') for col in columns_name] #변별력
X_df = pd.DataFrame(data = data, columns = columns_name)
y_df = pd.DataFrame(data = target, columns = ['label'])
df = pd.concat([X_df, y_df], axis = 1)
df['label'] = df['label'].replace([0, 1], [1, 0])
df
#############################################
mean_radius mean_texture mean_perimeter mean_area mean_smoothness mean_compactness mean_concavity mean_concave_points mean_symmetry mean_fractal_dimension label
0 17.99 10.38 122.80 1001.0 0.11840 0.27760 0.30010 0.14710 0.2419 0.07871 1
1 20.57 17.77 132.90 1326.0 0.08474 0.07864 0.08690 0.07017 0.1812 0.05667 1
2 19.69 21.25 130.00 1203.0 0.10960 0.15990 0.19740 0.12790 0.2069 0.05999 1
3 11.42 20.38 77.58 386.1 0.14250 0.28390 0.24140 0.10520 0.2597 0.09744 1
4 20.29 14.34 135.10 1297.0 0.10030 0.13280 0.19800 0.10430 0.1809 0.05883 1
... ... ... ... ... ... ... ... ... ... ... ...
564 21.56 22.39 142.00 1479.0 0.11100 0.11590 0.24390 0.13890 0.1726 0.05623 1
565 20.13 28.25 131.20 1261.0 0.09780 0.10340 0.14400 0.09791 0.1752 0.05533 1
566 16.60 28.08 108.30 858.1 0.08455 0.10230 0.09251 0.05302 0.1590 0.05648 1
567 20.60 29.33 140.10 1265.0 0.11780 0.27700 0.35140 0.15200 0.2397 0.07016 1
568 7.76 24.54 47.92 181.0 0.05263 0.04362 0.00000 0.00000 0.1587 0.05884 0

569 rows × 11 columns

<svg xmlns="http://www.w3.org/2000/svg" height="24px"viewBox="0 0 24 24"
width="24px">



b. 데이터를 바탕으로 로지스틱 회귀식을 구하시오.

  • 이때, 독립변수: mean_radius
#############################################
model = smf.logit('label ~ mean_radius', data = df).fit()
model.summary()
#############################################
Optimization terminated successfully.
         Current function value: 0.289992
         Iterations 8
Logit Regression Results
Dep. Variable: label No. Observations: 569
Model: Logit Df Residuals: 567
Method: MLE Df Model: 1
Date: Sun, 18 Jun 2023 Pseudo R-squ.: 0.5608
Time: 14:28:43 Log-Likelihood: -165.01
converged: True LL-Null: -375.72
Covariance Type: nonrobust LLR p-value: 1.192e-93
coef std err z P>|z| [0.025 0.975]
Intercept -15.2459 1.325 -11.509 0.000 -17.842 -12.649
mean_radius 1.0336 0.093 11.100 0.000 0.851 1.216

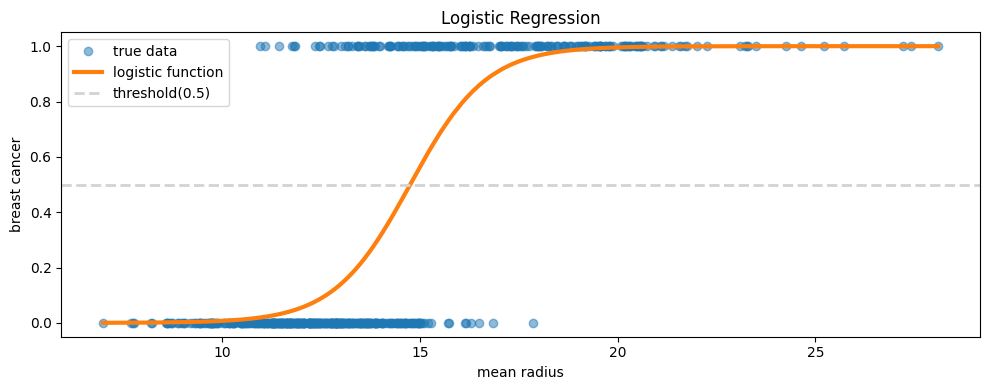
c. 실제 데이터와 로지스틱 회귀선을 한 그림에 겹쳐서 그릴 것.

plt.figure(figsize=(10, 4))

####################################################################
sorted_x = df['mean_radius'].sort_values() #데이터 시각화를 위한 x값 오름차순 정렬
y = 1/(1+np.exp(15.2459 - 1.0336 * sorted_x)) # 데이터 x를 우리가 구한 로지스틱함수를 통해 y 값구하기
plt.plot(df['mean_radius'], df['label'], 'o', alpha = 0.5, label = 'true data') #실제 데이터
plt.plot(sorted_x, y, label = 'logistic function', linewidth = 3) #우리가 추측한 로지스틱 함수
plt.axhline(0.5, color='lightgray', linestyle='--', linewidth=2, label = 'threshold(0.5)')
plt.title('Logistic Regression')
plt.legend()
plt.xlabel('mean radius')
plt.ylabel('breast cancer')
plt.tight_layout()
####################################################################

정답

a. y^=11+e15.2459−1.0336xradius\hat{y} = \frac{1}{1+e^{15.2459 - 1.0336x_{radius}}}

b. Logit = -15.2459 + 1.0336x_{radius} -> 종양의 반지름이 1mm 증가하면 암에 걸릴 확률의 로짓값이 1.0336 증가한다.

c. Odds Ratio: 2.811 -> 종양의 반지름이 1mm 증가하면 암에 걸릴 확률의 오즈가 2.811배 증가한다.

문제3. Poisson / Negative Binomial Regression (35점)

a. 주어진 데이터를 데이터프레임화 하기 (DataFrame) (10점)
b. 푸아송 회귀모델과 음이항 회귀모델 중 어떤 모델을 선택할 것인지 이유와 함께 제시하라.
    - 이때, 알파값에 대한 가설검정의 유의수준은 0.05로하며, 독립변수는 High Temp (°F) 와 Precipitation 만 사용할 것.(10점)
c. 데이터를 바탕으로 선택한 회귀모델의 회귀식을 구하시오. High Temp (°F) 와 Precipitation(5점)
d. 유의수준 0.05에서 유의미하다고 판단되는 독립변수를 찾고, 해당 변수의 IRR(Incidence Rate Ratio)을 구하고, 의미를 해석하시오. (10점)

날씨에 따른 하루동안 다리(bridge)를 지나가는 자전거 수 데이터

종속변수

  • Manhattan Bridge: 하루동안 맨하튼 다리를 건너는 자전거 수

독립변수

  • Date: 날짜
  • Day: 날짜
  • High Temp (°F) : 최고온도 (단위: 도)
  • Low Temp (°F): 최저온도
  • Precipitation: 강수량 (단위: mm)
  • Brooklyn Bridge: 하루동안 브루클린 다리를 건너는 자전거 수
  • Williamsburg Bridge: 하루동안 윌리엄스버그 다리를 건너는 자전거 수
  • Queensboro Bridge: 하루동안 퀸스보로 다리를 건너는 자전거 수
#######이 셀을 실행하면 데이터가 받아집니다. 실행만 하고 이 셀을 변형시키려 하지 마세요.###########
df = pd.read_csv('https://raw.githubusercontent.com/ericoh929/Machine-Learning/main/nyc-east-river-bicycle-counts.csv')
df.drop(['Total'], axis = 1, inplace = True)
df.replace({'Precipitation':'0.47 (S)'}, 0.47, inplace = True)
df.replace({'Precipitation':'T'}, 0, inplace = True)
df
Unnamed: 0 Date Day High Temp (°F) Low Temp (°F) Precipitation Brooklyn Bridge Manhattan Bridge Williamsburg Bridge Queensboro Bridge
0 0 2016-04-01 00:00:00 2016-04-01 00:00:00 78.1 66.0 0.01 1704.0 3126 4115.0 2552.0
1 1 2016-04-02 00:00:00 2016-04-02 00:00:00 55.0 48.9 0.15 827.0 1646 2565.0 1884.0
2 2 2016-04-03 00:00:00 2016-04-03 00:00:00 39.9 34.0 0.09 526.0 1232 1695.0 1306.0
3 3 2016-04-04 00:00:00 2016-04-04 00:00:00 44.1 33.1 0.47 521.0 1067 1440.0 1307.0
4 4 2016-04-05 00:00:00 2016-04-05 00:00:00 42.1 26.1 0 1416.0 2617 3081.0 2357.0
... ... ... ... ... ... ... ... ... ... ...
205 205 2016-04-26 00:00:00 2016-04-26 00:00:00 60.1 46.9 0.24 1997.0 3520 4559.0 2929.0
206 206 2016-04-27 00:00:00 2016-04-27 00:00:00 62.1 46.9 0 3343.0 5606 6577.0 4388.0
207 207 2016-04-28 00:00:00 2016-04-28 00:00:00 57.9 48.0 0 2486.0 4152 5336.0 3657.0
208 208 2016-04-29 00:00:00 2016-04-29 00:00:00 57.0 46.9 0.05 2375.0 4178 5053.0 3348.0
209 209 2016-04-30 00:00:00 2016-04-30 00:00:00 64.0 48.0 0 3199.0 4952 5675.0 3606.0

210 rows × 10 columns

<svg xmlns="http://www.w3.org/2000/svg" height="24px"viewBox="0 0 24 24"
width="24px">



a. 주어진 데이터를 테이터프레임화 하기. (10점)

  • 컬럼명 사이에 띄어쓰기가 되어 있는데 (ex, Brooklyn Bridge) 띄어쓰기를 없애고 underbar 로 대체할 것. (ex, Brooklyn_Bridge)
  • 컬럼명에 있는 화씨 표시를 없앨 것 (°F)
  • Precipitation 컬럼이 문자열 타입으로 되어 있는데, 실수형 타입으로 바꿀 것.
#################################################################
df.columns = [col.replace(' ', '_') for col in df.columns]
df.rename(columns = {'High_Temp_(°F)': 'High_Temp', 'Low_Temp_(°F)': 'Low_Temp'}, inplace = True)
df = df.astype({'Precipitation':'float'})
df
#################################################################
Unnamed:_0 Date Day High_Temp Low_Temp Precipitation Brooklyn_Bridge Manhattan_Bridge Williamsburg_Bridge Queensboro_Bridge
0 0 2016-04-01 00:00:00 2016-04-01 00:00:00 78.1 66.0 0.01 1704.0 3126 4115.0 2552.0
1 1 2016-04-02 00:00:00 2016-04-02 00:00:00 55.0 48.9 0.15 827.0 1646 2565.0 1884.0
2 2 2016-04-03 00:00:00 2016-04-03 00:00:00 39.9 34.0 0.09 526.0 1232 1695.0 1306.0
3 3 2016-04-04 00:00:00 2016-04-04 00:00:00 44.1 33.1 0.47 521.0 1067 1440.0 1307.0
4 4 2016-04-05 00:00:00 2016-04-05 00:00:00 42.1 26.1 0.00 1416.0 2617 3081.0 2357.0
... ... ... ... ... ... ... ... ... ... ...
205 205 2016-04-26 00:00:00 2016-04-26 00:00:00 60.1 46.9 0.24 1997.0 3520 4559.0 2929.0
206 206 2016-04-27 00:00:00 2016-04-27 00:00:00 62.1 46.9 0.00 3343.0 5606 6577.0 4388.0
207 207 2016-04-28 00:00:00 2016-04-28 00:00:00 57.9 48.0 0.00 2486.0 4152 5336.0 3657.0
208 208 2016-04-29 00:00:00 2016-04-29 00:00:00 57.0 46.9 0.05 2375.0 4178 5053.0 3348.0
209 209 2016-04-30 00:00:00 2016-04-30 00:00:00 64.0 48.0 0.00 3199.0 4952 5675.0 3606.0

210 rows × 10 columns

<svg xmlns="http://www.w3.org/2000/svg" height="24px"viewBox="0 0 24 24"
width="24px">



b. 푸아송 회귀모델을 선택할 것인가, 음이항 회귀모델을 선택할 것인가. (10점)

##############################################
model = smf.negativebinomial('Manhattan_Bridge ~ High_Temp + Precipitation', data = df).fit()
model.summary()
##############################################
Optimization terminated successfully.
         Current function value: 8.326608
         Iterations: 14
         Function evaluations: 24
         Gradient evaluations: 24
NegativeBinomial Regression Results
Dep. Variable: Manhattan_Bridge No. Observations: 210
Model: NegativeBinomial Df Residuals: 207
Method: MLE Df Model: 2
Date: Sun, 18 Jun 2023 Pseudo R-squ.: 0.06475
Time: 14:42:32 Log-Likelihood: -1748.6
converged: True LL-Null: -1869.6
Covariance Type: nonrobust LLR p-value: 2.662e-53
coef std err z P>|z| [0.025 0.975]
Intercept 6.7311 0.122 55.127 0.000 6.492 6.970
High_Temp 0.0267 0.002 13.819 0.000 0.023 0.030
Precipitation -2.2994 0.187 -12.298 0.000 -2.666 -1.933
alpha 0.0749 0.007 10.323 0.000 0.061 0.089

정답

a. y^=e6.7311+0.0267xhightemp−2.2994xprecipitation\hat{y} = e^{6.7311 + 0.0267x_{hightemp} - 2.2994x_{precipitation}}

b. High Temp, Precipitation -> 각각 1.027, 0.1003 의 IRR 을 구할 수 있다.

- High Temp: 하루의 최고 온도가 1도 증가하면 하루동안 맨하튼 다리를 건너는 자전거 수는 1.027배 증가한다.
- Precipitation: 하루의 강수량이 1mm 증가하면 하루동안 맨하튼 다리를 건너는 자전거 수는 0.1003배 증가한다.
np.exp(-3.7714)
0.023019812979106692
import seaborn as sns
C1 = [93.76, 93.16, 88.54, 82.52, 81.56, 79.88, 72.7, 72.36, 71.38, 71.16, 67.92, 67.1, 65.82, 62.82, 62.58, 62.1, 58.56, 56.78, 45.24]
A1 = [98.32, 93.86, 93.48, 89.2, 81.64, 81.34, 79.56, 73.86, 72.7, 72.26, 70.16, 68.8, 66.78, 62.5, 60.82, 60.26, 53.26, 44.04]
D1 = [89.3, 95.2, 90.7, 91, 86.4, 82.4, 89.4, 94.3, 80, 89.3, 93.7, 87.5, 93.6, 88, 92.7, 87.2, 95.1, 87.1, 94.8]
sns.boxplot(D1)

np.mean(A1)
73.49111111111111
profile
Jihwan Oh
Deep Learning, Multi-Agent RL, Large Language Model, Statistics
이전 포스트

Linear Regression exercise (선형회귀 실전문제)

0개의 댓글

관련 채용 정보