연속확률분포(정규분포)

라이브러리 불러오기

from scipy.stats import norm #정규분포

import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm #정규확률그림

norm.cdf, ppf 예시

print(norm.cdf(x = 1, loc = 0, scale = 1)) #정규분포의 누적확률
print(norm.ppf(q=0.84134, loc = 0, scale = 1)) #정규분포의 백분위수

0.8413447460685429
0.9999803859660787

예시) 기본적으로 정규확률그림에서 데이터가 선 위에 있으면 정규확률의 가정을 따른다고 판단

data = np.array([4001, 3927, 3048, 4298, 4000, 3445, 4949, 3530, 3075, 4012, 3797,
                 3550, 4027, 3571, 3738, 5157, 3598, 4749, 4263, 3894, 4262, 4232,
                 3852, 4256, 3271, 4315, 3078, 3607, 3889, 3147, 3421, 3531, 3987,
                 4120, 4349, 4071, 3683, 3332, 3285, 3739, 3544, 4103, 3401, 3601,
                 3717, 4846, 5005, 3991, 2866, 3561, 4003, 4387, 3510, 2884, 3819,
                 3173, 3470, 3340, 3214, 3370, 3694])

histogram

plt.hist(data, bins = 7, color = 'red', alpha = 0.4)
plt.xlabel('data')
plt.ylabel('density')
plt.title('histogram of data')
plt.show()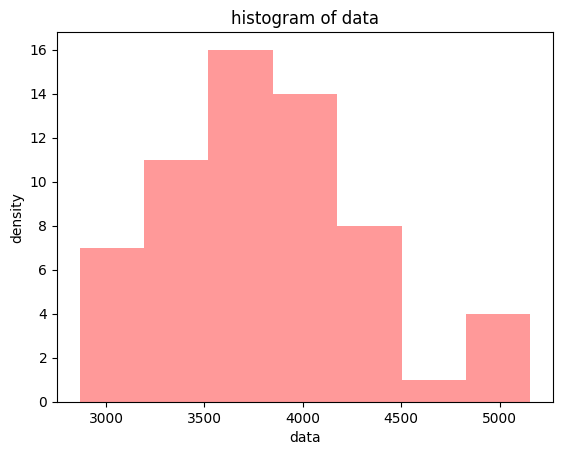

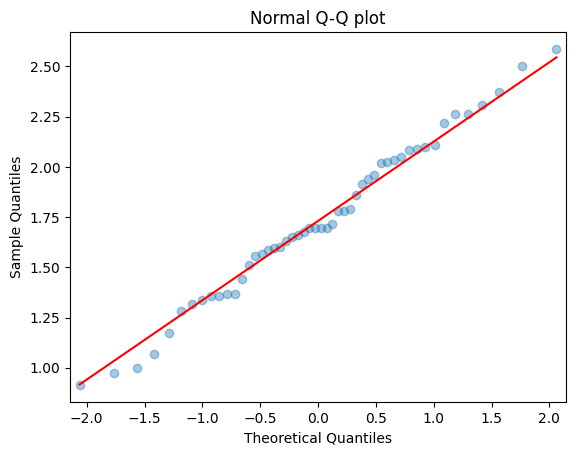
정규확률그림

sm.qqplot(data, line = 's', alpha = 0.4)
plt.title("Normal Q-Q plot")
plt.show()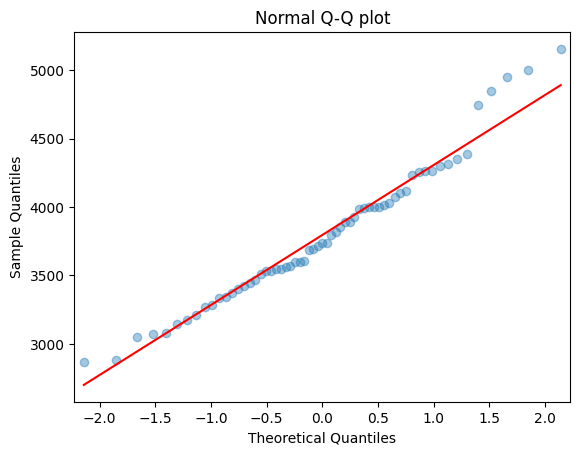

예제 13

data_tree = np.array([39.3, 14.8, 6.3, 3.0, 0.9, 6.5,
                 3.5, 8.3, 10.0, 1.3, 7.1,
                 6.0, 17.1, 16.8, 0.7, 7.9,
                 2.7, 26.2, 24.3, 17.7, 3.2,
                 7.4, 6.6, 5.2, 8.3, 5.9,
                 3.5, 8.3, 44.8, 8.3, 13.4,
                 19.4, 19.0, 14.1, 1.9, 12.0,
                 19.7, 10.3, 3.4, 16.7, 4.3,
                 1.0, 7.6, 28.3, 26.2, 31.7,
                 8.7, 18.9, 3.4, 10.0])

histogram

plt.hist(data_tree, bins = 5, range=(0, 50), color = 'red', alpha = 0.3)
plt.xlabel('data')
plt.ylabel('density')
plt.title('Histogram of data')
plt.show()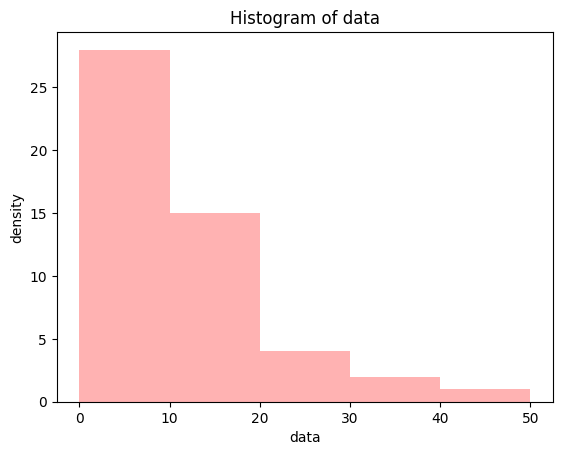

sm.qqplot(data_tree, line = 's', alpha = 0.4)
plt.title('Normal Q-Q plot')
plt.show()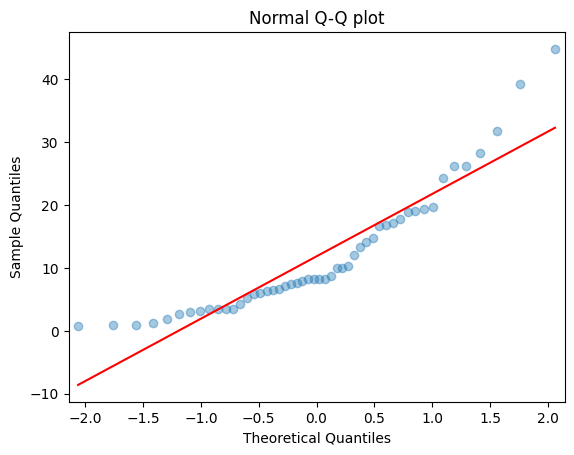

제곱근 데이터

datatree_sqrt = np.sqrt(data_tree)

plt.hist(datatree_sqrt, bins = 5, range=(0, 8), color = 'red', alpha = 0.3)
plt.xlabel('data')
plt.ylabel('density')
plt.title('Histogram of data')
plt.show()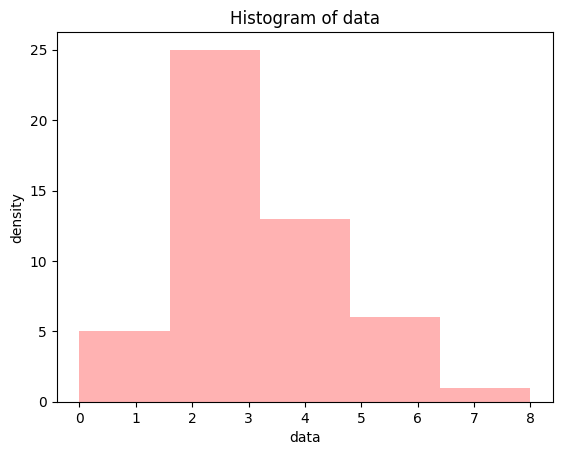

sm.qqplot(datatree_sqrt, line = 's', alpha = 0.4)
plt.show()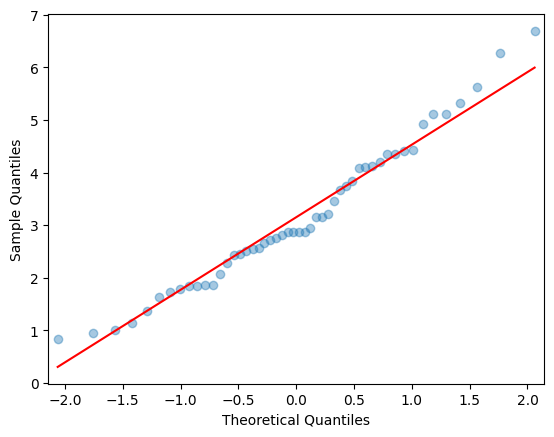

네제곱근 데이터

datatree_4 = np.power(data_tree, 0.25)

plt.hist(datatree_4, bins = 5, range=(0.5, 3), color = 'red', alpha = 0.3)
plt.xlabel('data')
plt.ylabel('density')
plt.title('Histogram of data')
plt.show()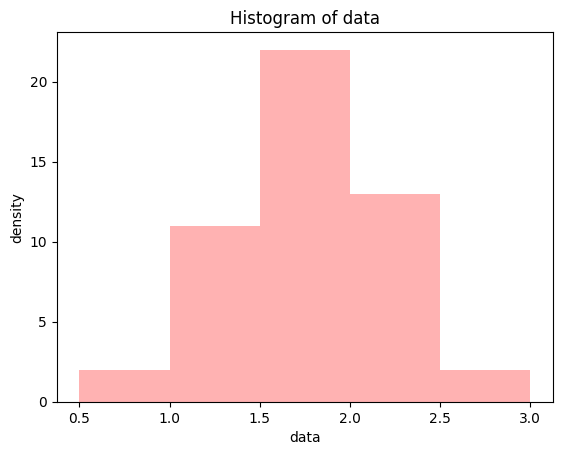

sm.qqplot(datatree_4, line = 's', alpha = 0.4)
plt.title('Normal Q-Q plot')

Text(0.5, 1.0, 'Normal Q-Q plot')