RD Curve

RD Curve는 Image Compression분야 논문에서 모델의 성능을 평가하기 위한 지표로 사용되는 그래프이다.

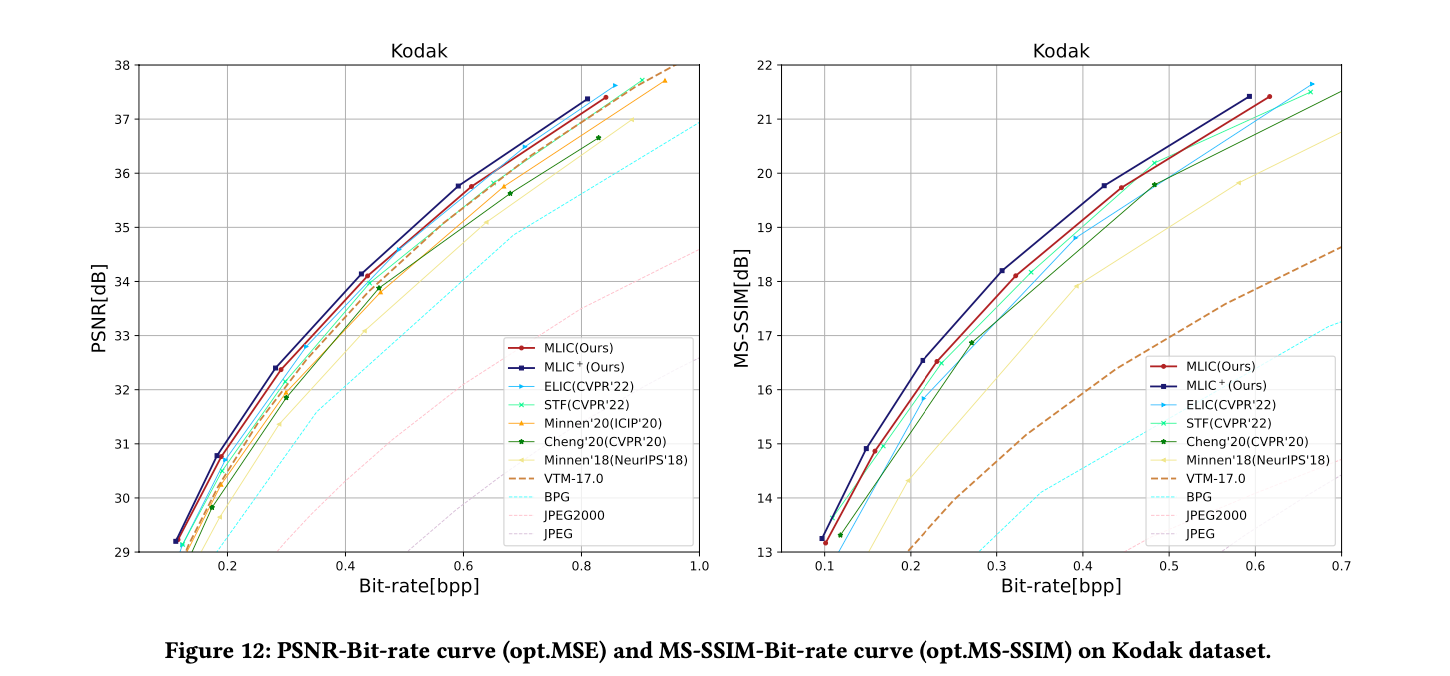
MLIC: Multi-Reference Entropy Model for Learned Image Compression

위와 같이 보통 우상향하는 곡선이 나타나게 된다.
X축은 BPP(Bit per pixel)를 고정으로 사용하며, Y축은 이미지 품질을 평가하는 PSNR(Peak signal-to-noise ratio), SSIM(Structural Similiarity Index Measure), MS-SSIM(Multi-Scale Structural Similiarity Index Measure)를 사용한다.

RD Curve에서 낮은 BPP에 대하여 이미지 품질 평가척도가 상대적으로 좋다면 좋은 모형이라고 할 수 있습니다. 즉, 고품질의 이미지를 보다 적은 용량으로 저장할 수 있다.

Python Code

bpp - PSNR

전통적인 압축 방법인 JPEG 압축 결과에대헌 RD Curve를 파이썬으로 구현 코드이다.

레나 이미지 다운로드
https://github.com/mikolalysenko/lena/blob/master/lena.png

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
import io
import os

# 이미지 불러오기
image_path = './lena.png'
original_image = Image.open(image_path)

# JPEG 압축 후 PSNR 계산
def compress_image(image, quality):
    # Compress image
    buffer = io.BytesIO()
    image.save(buffer, format="JPEG", quality=quality)
    compressed_image = Image.open(buffer).convert('RGB')

    # PSNR 계산
    mse = np.mean((np.array(image) - np.array(compressed_image)) ** 2)
    if mse == 0:
        return compressed_image, 100
    psnr = 20 * np.log10(255 / np.sqrt(mse))
    return compressed_image, psnr

# 이미지품질 파라미터 설정
qualities = list(range(5, 101, 5)) # 5 ~ 100 사이의 값 중 5씩 증가  [5, 10, 15, ..., 100]
psnr_values = []
sizes = []

for quality in qualities:
    _, psnr = compress_image(original_image, quality)
    psnr_values.append(psnr)

    # 이미지 크기 계산
    buffer = io.BytesIO()
    original_image.save(buffer, format="JPEG", quality=quality)
    size = buffer.tell()
    sizes.append(size)

# 이미지 크기를 비트로 변환 (1바이트 = 8비트) -> 비트당 픽셀 수 계산 -> bpp 계산
width, height = original_image.size
total_pixels = width * height
bits_per_pixel = [size * 8 / total_pixels for size in sizes]

# 뒤에서 2개날리기
bits_per_pixel = bits_per_pixel[:-2]
psnr_values = psnr_values[:-2]


# RD Curve 그리기
plt.figure(figsize=(10, 5))
plt.plot(bits_per_pixel, psnr_values, marker='o')
plt.title('RD Curve - PSNR')
plt.xlabel('Bits Per Pixel (bpp)')
plt.ylabel('PSNR (dB)')
plt.legend(['JPEG'], loc='lower right')
plt.grid(True)
plt.show()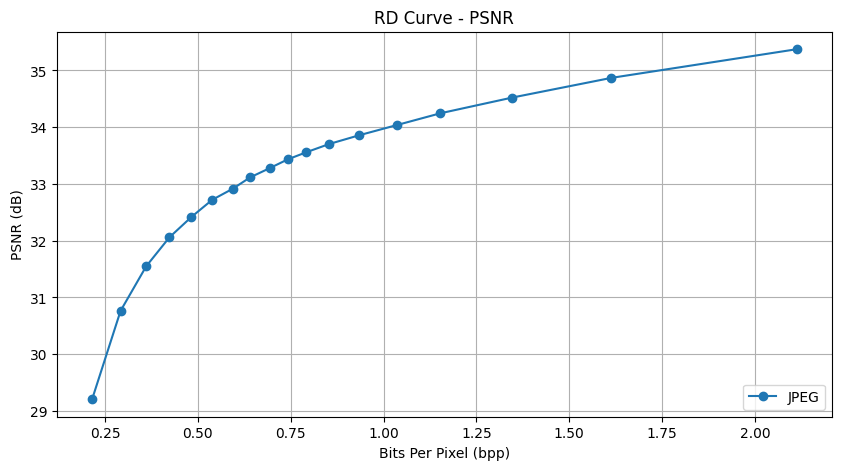

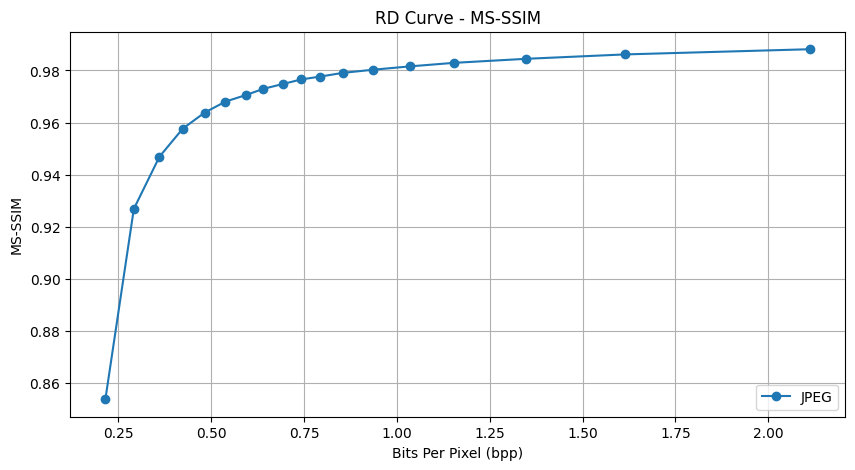
bpp - MS-SSIM

두 이미지 간 MS-SSIM을 계산은 sewar라는 파이썬 라이브러리를 사용하였다.

sewar 라이브러리
https://towardsdatascience.com/measuring-similarity-in-two-images-using-python-b72233eb53c6

설치 명령어
pip install sewar

from skimage.metrics import structural_similarity as ssim
import math
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
import io
import os
from sewar.full_ref import mse, rmse, psnr, uqi, ssim, ergas, scc, rase, sam, msssim, vifp
import warnings 
warnings.filterwarnings('ignore')

# 이미지 불러오기
image_path = './lena.png'
original_image = Image.open(image_path)


# JPEG 압축 후 MS-SSIM 계산
def compress_image_msssim(image, quality):
    # Compress image
    buffer = io.BytesIO()
    image.save(buffer, format="JPEG", quality=quality)
    compressed_image = Image.open(buffer)
    compressed_image_array = np.array(compressed_image)

    # MS-SSIM 계산
    msssim_value = msssim(np.array(image), compressed_image_array)

    return compressed_image, msssim_value

msssim_values = []
qualities = list(range(5, 101, 5)) # 5 ~ 100 사이의 값 중 5씩 증가  [5, 10, 15, ..., 100]
sizes = []
for quality in qualities:
    _, msssim2 = compress_image_msssim(original_image, quality)
    msssim_values.append(msssim2)
    buffer = io.BytesIO()
    original_image.save(buffer, format="JPEG", quality=quality)
    size = buffer.tell()
    sizes.append(size)



# 이미지 크기를 비트로 변환 (1바이트 = 8비트) -> 비트당 픽셀 수 계산 -> bpp 계산
width, height = original_image.size
total_pixels = width * height
bits_per_pixel = [size * 8 / total_pixels for size in sizes]
# 뒤에서 2개 날리기 
bits_per_pixel = bits_per_pixel[:-2]
msssim_values = msssim_values[:-2]

# RD Curve 그리기
plt.figure(figsize=(10, 5))
plt.plot(bits_per_pixel, msssim_values, marker='o')
plt.title('RD Curve - MS-SSIM')
plt.xlabel('Bits Per Pixel (bpp)')
plt.ylabel('MS-SSIM')
plt.legend(['JPEG'], loc='lower right')
plt.grid(True)
plt.show()