학습기반 이미지 압축 논문을 보면서 가장 많이 살펴보는데 아래 RD-Curve 일 것이다.
왜냐면 모델의 성능을 한 눈에 직관적으로 알 수 있는 방법이기 때문이다.

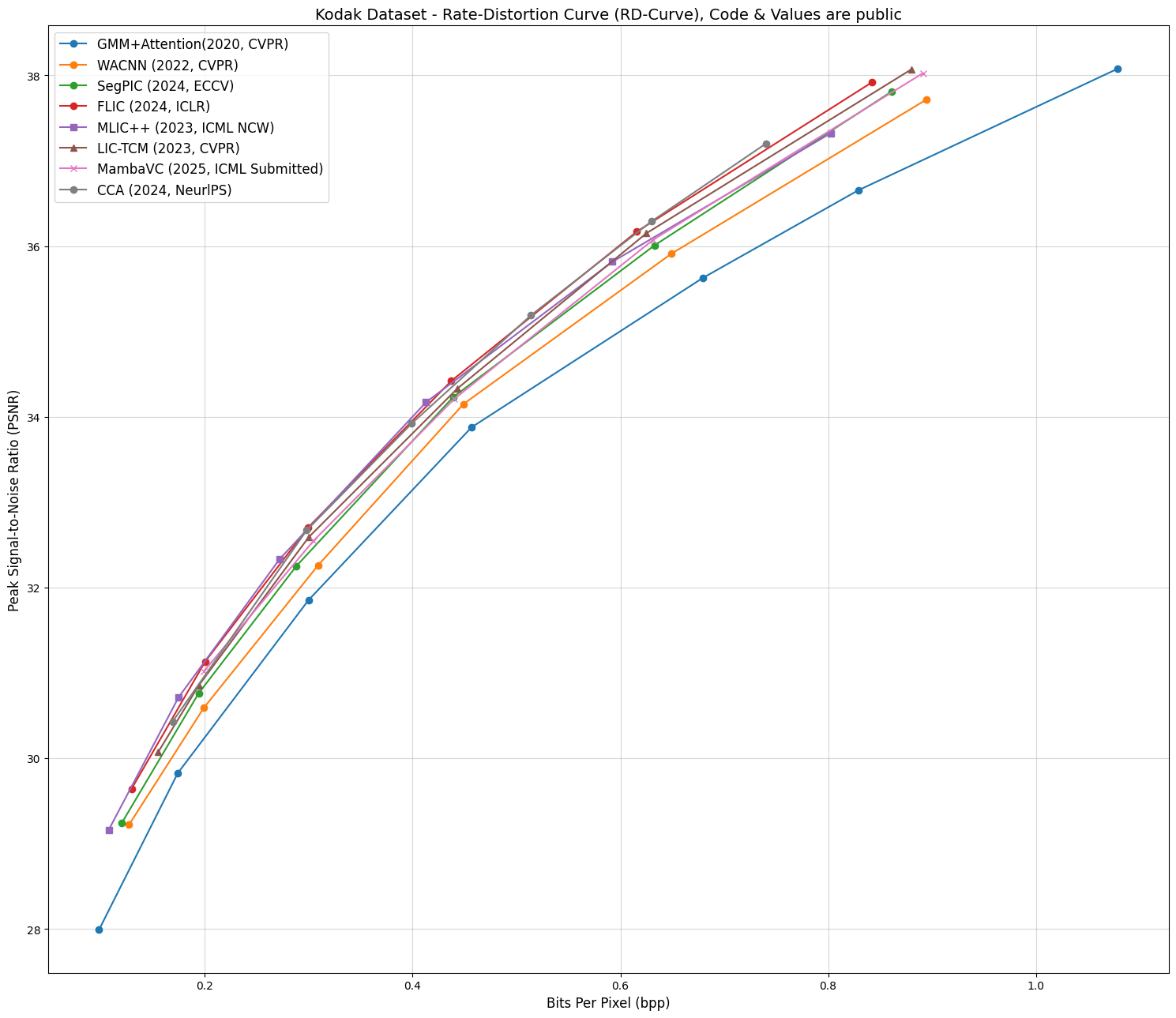
그래프를 보면 알 수 있듯이 제안 모델이 비교 모델보다 더 위에 있다 => 더 좋은 모델이다.
이걸 한 번에 알 수 있는 Figure이다.

하지만 근래 BD-Rate를 공부하면서 눈으로본 RD-Curve와는 다른 평가 결과가 나와서 코드와 같이 알아보고자 한다.

import matplotlib.pyplot as plt


cca_bpp = [0.740, 0.630, 0.514, 0.399, 0.298, 0.169]
cca_psnr = [37.20, 36.29, 35.19, 33.92, 32.67, 30.43]

stf_bpp = [0.127, 0.199, 0.309, 0.449, 0.649, 0.895]
stf_psnr = [29.22, 30.59, 32.26, 34.15, 35.91, 37.72]

# 데이터 입력
bpp_1 = [0.1294, 0.2003, 0.2993, 0.4372, 0.6158, 0.842]
psnr_1 = [29.64, 31.132, 32.702, 34.42, 36.17, 37.918]

bpp_2 = [0.1075, 0.1747, 0.2721, 0.4129, 0.5923, 0.8025]
psnr_2 = [29.161, 30.7137, 32.3345, 34.1702, 35.8161, 37.3229]

bpp_3 = [0.155, 0.194, 0.300, 0.443, 0.625, 0.880]
psnr_3 = [30.07, 30.85, 32.59, 34.33, 36.15, 38.07]

gmm_bpp = [0.098115338, 0.173912113,0.299725056, 0.456783226, 0.679351191, 0.829, 1.079]
gmm_psnr = [	27.9897452, 	29.8244, 	31.851, 	33.8773766, 35.62697935, 	36.654, 	38.08]

segpic_bpp = [0.120, 0.194, 0.288, 0.439, 0.633, 0.861]
segpic_psnr = [29.24, 30.76, 32.25, 34.23, 36.01, 37.81]


x_values = [0.891213389, 0.631520223, 0.440167364, 0.30446304, 0.19902371]
y_values = [38.02570573, 36.07381748, 34.20996183, 32.54554182, 31.01809218]

# 그래프 그리기
plt.figure(figsize=(15, 13))
plt.plot(gmm_bpp, gmm_psnr, marker='o', label='GMM+Attention(2020, CVPR)')
plt.plot(stf_bpp, stf_psnr, marker='o', label='WACNN (2022, CVPR)')
plt.plot(segpic_bpp, segpic_psnr, marker='o', label='SegPIC (2024, ECCV)')
plt.plot(bpp_1, psnr_1, marker='o', label='FLIC (2024, ICLR)')
plt.plot(bpp_2, psnr_2, marker='s', label='MLIC++ (2023, ICML NCW)')
plt.plot(bpp_3, psnr_3, marker='^', label='LIC-TCM (2023, CVPR)')
plt.plot(x_values, y_values, marker='x', label='MambaVC (2025, ICML Submitted)')
plt.plot(cca_bpp, cca_psnr, marker='o', label='CCA (2024, NeurlPS)')
# 그래프 설정
plt.xlabel('Bits Per Pixel (bpp)', fontsize=12)
plt.ylabel('Peak Signal-to-Noise Ratio (PSNR)', fontsize=12)
plt.title('Kodak Dataset - Rate-Distortion Curve (RD-Curve), Code & Values are public', fontsize=14)
plt.grid(alpha=0.5)
plt.legend(fontsize=12)
plt.tight_layout()

# 그래프 출력
plt.show()

위 그래프의 코드이며, SOTA라고 생각했던 모델들 중에 깃허브 레포와 RD data를 공개하는 모델만 정리했다.
공개를 하지않으면 내가 다 돌려서 확인해야하기에 너무 귀찮다,,,

특이사항으로 GMM+Attention 모델의 마지막 평가값은 임의로 추가한 값이다.
공식 레포에는 없는 값이다.

Bjontegaard metric

https://github.com/Anserw/Bjontegaard_metric

BD-Rate에 대해 알아야하는데 이론은 아래 블로그에서 친절하게 설명해준다.
코드는 위 깃허브 레포를 사용했다.

https://medium.com/innovation-labs-blog/bjontegaard-delta-rate-metric-c8c82c1bc42c

import numpy as np
import scipy.interpolate

def BD_PSNR(R1, PSNR1, R2, PSNR2, piecewise=0):
    lR1 = np.log(R1)
    lR2 = np.log(R2)

    PSNR1 = np.array(PSNR1)
    PSNR2 = np.array(PSNR2)

    p1 = np.polyfit(lR1, PSNR1, 3)
    p2 = np.polyfit(lR2, PSNR2, 3)

    # integration interval
    min_int = max(min(lR1), min(lR2))
    max_int = min(max(lR1), max(lR2))

    # find integral
    if piecewise == 0:
        p_int1 = np.polyint(p1)
        p_int2 = np.polyint(p2)

        int1 = np.polyval(p_int1, max_int) - np.polyval(p_int1, min_int)
        int2 = np.polyval(p_int2, max_int) - np.polyval(p_int2, min_int)
    else:
        # See https://chromium.googlesource.com/webm/contributor-guide/+/master/scripts/visual_metrics.py
        lin = np.linspace(min_int, max_int, num=100, retstep=True)
        interval = lin[1]
        samples = lin[0]
        v1 = scipy.interpolate.pchip_interpolate(np.sort(lR1), PSNR1[np.argsort(lR1)], samples)
        v2 = scipy.interpolate.pchip_interpolate(np.sort(lR2), PSNR2[np.argsort(lR2)], samples)
        # Calculate the integral using the trapezoid method on the samples.
        int1 = np.trapz(v1, dx=interval)
        int2 = np.trapz(v2, dx=interval)

    # find avg diff
    avg_diff = (int2-int1)/(max_int-min_int)

    # 소수 둘째자리까지 출력
    avg_diff = round(avg_diff, 2)
    return avg_diff


def BD_RATE(R1, PSNR1, R2, PSNR2, piecewise=0):
    lR1 = np.log(R1)
    lR2 = np.log(R2)

    # rate method
    p1 = np.polyfit(PSNR1, lR1, 3)
    p2 = np.polyfit(PSNR2, lR2, 3)

    # integration interval
    min_int = max(min(PSNR1), min(PSNR2))
    max_int = min(max(PSNR1), max(PSNR2))

    # find integral
    if piecewise == 0:
        p_int1 = np.polyint(p1)
        p_int2 = np.polyint(p2)

        int1 = np.polyval(p_int1, max_int) - np.polyval(p_int1, min_int)
        int2 = np.polyval(p_int2, max_int) - np.polyval(p_int2, min_int)
    else:
        lin = np.linspace(min_int, max_int, num=100, retstep=True)
        interval = lin[1]
        samples = lin[0]
        v1 = scipy.interpolate.pchip_interpolate(np.sort(PSNR1), lR1[np.argsort(PSNR1)], samples)
        v2 = scipy.interpolate.pchip_interpolate(np.sort(PSNR2), lR2[np.argsort(PSNR2)], samples)
        # Calculate the integral using the trapezoid method on the samples.
        int1 = np.trapz(v1, dx=interval)
        int2 = np.trapz(v2, dx=interval)

    # find avg diff
    avg_exp_diff = (int2-int1)/(max_int-min_int)
    avg_diff = (np.exp(avg_exp_diff)-1)*100
    
    # 소수 둘째자리까지 출력
    avg_diff = round(avg_diff, 2)
    return avg_diff

코드는 위 코드를 사용했다. 깃허브 별이 100개 넘어서 공신력있는 코드라 생각해서 검증없이 사용했다.

결과

# BD-Rate 계산
models = {
    "FLIC (2024)": (bpp_1, psnr_1),
    "MLIC++ (2023)": (bpp_2, psnr_2),
    "CCA (2024)": (cca_bpp, cca_psnr),
    "LIC-TCM (2023)": (bpp_3, psnr_3),
    "MambaVC (2025)": (x_values, y_values),
    "SegPIC (2024)": (segpic_bpp, segpic_psnr),
    "WACNN (2022)": (stf_bpp, stf_psnr),

}

bd_rate_results = {
    model_name: BD_RATE(gmm_bpp, gmm_psnr, bpp, psnr)
    for model_name, (bpp, psnr) in models.items()
}

# 결과 출력
bd_rate_results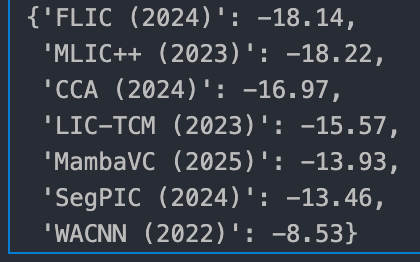

BD-rate는 가장 성능이 낮은 모델인 2020년 CVPR 논문을 기준으로 계산했다.
결과를 살펴보면

1. MLIC++
2. FLIC
3. CCA
4. LIC-TCM
5. MambaVC
6. SegPIC
7. WACNN (아마 STF도 이쯤,,)

순으로 나타났고, paper with code에 랭크되어있는 MLIC++가 아직까진 미세한 차이로 SOTA를 달성했다.
VVC로 테스트하면 역전될지 의문이 생기기도한다.
왜냐하면 그래프로보면 값이 큰 람다는 FLIC나 LIC-TCM이 MLIC++보다 더 높은 지표를 가짐에도 BD-rate는 MLIC++가 더 좋게 나타났다. (물론 낮은 람다에선 MLIC++가 더 좋긴하다.)

결론

1. MLIC++는 2023년 모델임에도 Kodak 데이터셋에서 SOTA 자리를 지켰다.
2. 하지만 2024년에 좋은 모델들이 성능을 많이 끌어올렸다. 특히 FLIC..
3. Transformer를 깨부수기위해 나온 Mamba 기반 모델도 압축에선 아직 최적화되지 못한듯하다.
4. 졸업전까지만 안깨졌으면 좋겠다.

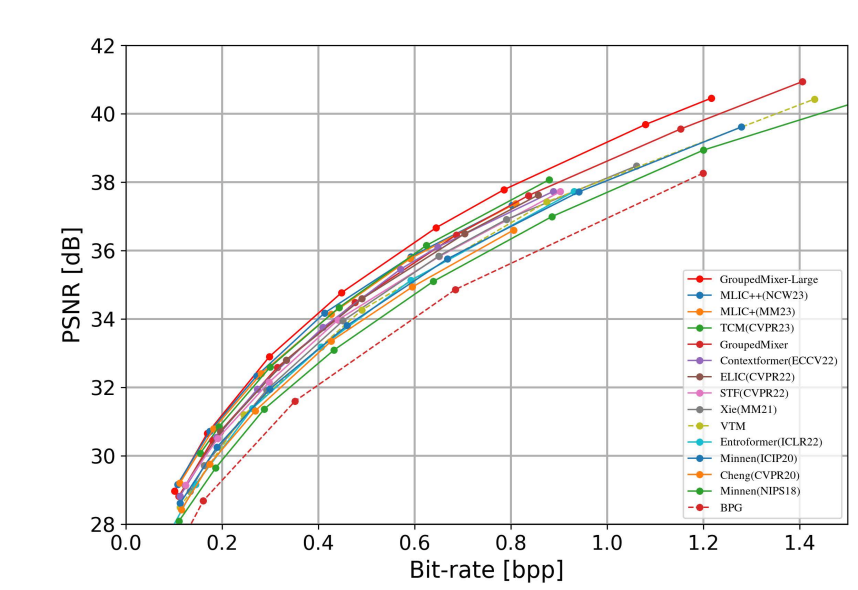
사실 비공식으로는 MLIC++는 1등에서 내려온 것 같다. 하지만 GroupedMixer 모델이 지금 깃허브 레포도 없고 RD-Data도 메일로 여쭤봐도 아직 답이 없으셔서,,, 포함은 시키지않았다.
-> 저널 Accept되면 공개하신다고 답장이 와서 추후 공개될 것 같다.