논문 제목
Frequency-Aware Transformer for Learned Image Compression (ICLR 2024 Poster)
URL: https://arxiv.org/abs/2310.16387
인용수 : 8회 (25.1.6 기준)

이전 포스트에서 최신 압축모델들의 BD-Rate를 비교한 결과 MLIC++(2023)다음으로 이 논문의 제안 모델인 FLIC, FTIC이었다.
그래서 이 논문에 대해 리뷰해보며 어떤 노벨티가 있는지 정리해보려합니다.

Abstract

• 기존의 LIC 방법은 anisotropic frequency component를 효과적으로 캡쳐하지 못하고, directional detail을 보존하는데 한계점이 있다.
• 이 문제를 해결하기 위해 frequency-aware transformer (FAT) block을 제안.
• FAT 블록은 multiscale과 directional frequency components를 캡쳐하기 위해 frequency-decomposition window attention (FDWA) 모듈로 구성된다.
• 그리고 frequency-modulation feed-forward network (FMFFN)을 통해 다양한 주파수 성분을 adaptively modulate하여 성능 향상.
• 마지막으로 transformer-based channel-wise autoregressive (T-CA) model을 제안하여 채널의 dependency를 효과적으로 활용했다고함.

정리해보자면 이 논문의 강점은 FAT블록, FMFFN, T-CA를 통한 효율적인 주파수 요소 캡쳐를 통한 성능향상이다.
이젠 좋은 논문이 되려면 제안 방법론이 2~3개는 되어야하는 것같다..

Related Work

Frequency Decomposition in Learned Image Compression

전통적인 이미지 코덱(image codec)은 subband decomposition을 사용하여 이미지의 주파수 성분 간 상관관계를 줄여서 컴팩트한 표현을 얻는다.
최근 LIC 방법 역시 explicit frequency decomposition으로부터 이점을 얻고 있다. iwave와 iwave++ 모델은 LIC에서 wavelet-like transform을 도입했지만, lifting scheme에 한정되며 네트워크 표현 능력을 저하시키고 latent space를 제한하는 한계가 있다.
Neural Image Compression via Attentional Multi-scale Back Projection and Frequency Decomposition 논문에서 입력 이미지의 저주파 및 고주파 성분을 별도로 처리하는 주파수 분해 모델을 제안.
Frequency disentangled features in neural image compression.에서는 HiLo attention을 활용하여 저주파와 고주파 성분을 분리했다.

하지만 이 방법론은 global self-attention으로 인해 큰 이미지 처리 시 계산 문제가 발생하며, directional decomposition를 구현하지 못했다.

Method

Overview

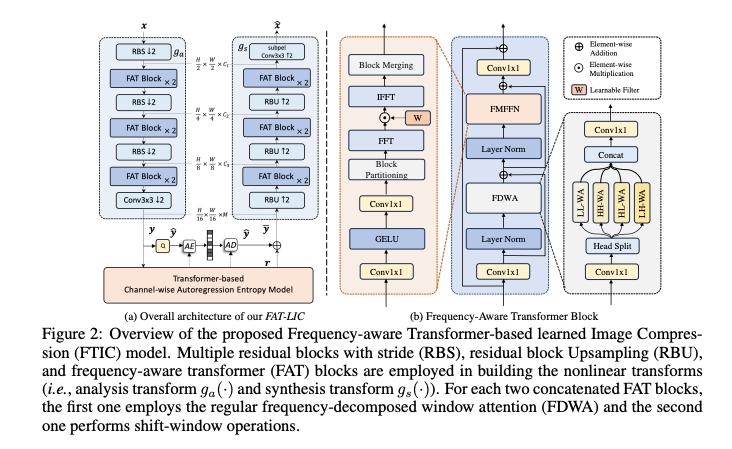
Fig 2는 Frequency-aware Transformer-based learned Image Compression (FTIC) 모델의 아키텍쳐이다.
다른 LIC모델과 동일한 플로우로 원본 이미지 $x$에 대해 인코더를 통과시켜 잠재표현 $y$로 매핑한다. 이후 양자화 연산 $Q(⋅)$을 통해 $\hat{y}$로 이산화시킨다. 이산화된 $\hat{y}$는 range coder에 의해 무손실로 인코딩된다.

대부분의 LIC는 $y$rk 평균 $\mu$와 Scale $\sigma$를 갖는 가우시안 분포를 따른다고 가정하며, 이 파라미터는 제안된 transformer-based channel-wise autoregressive (T-CA) entropy model에 의해 예측된다.

기존의 channel-wise autoregressive entropy model의 설정에 따라 $y$를 n개의 동일한 슬라이스로 나누고, 이러한 슬라이스를 T-CA 모델에 입력값으로 사용한다. 따라서, 인코딩된 슬라이스는 이후 슬라이스를 인코딩할 때 강력한 Context 정보를 제공한다.

Frequency-Aware Transformer (FAT) Block

본 논문의 목표는 이미지 압축 프레임워크 내에서 효율적인 주파수 분해를 구축하는 것이다. 이를 위해 naive multiscale and directional decomposition이 가능한 frequency-aware transformer (FAT) block을 제안한다.

FAT 블록은 frequency-decomposed window attention (FDWA) mechanism을 활용하여 입력 이미지를 저주파, 고주파 , 수직 및 수평 성분으로 분해한다. 이후 frequency-modulation feed-forward network (FMFFN)는 분해된 주파수 성분을 조정하여 성분 간 potential redundancy를 제거한다.

Frequency-Decomposed Window Attention (FDWA)

최근 연구는 일반적인 self-attention이 사실상 low-pass filter 역할을 하며, local window attention은 고주파 정보를 캡쳐할 수 있음을 보여주었다. 따라서, 다양한 window 크기를 활용하면 multiscale frequency components를 추출할 수 있다. 그러나 기존의 사각형 모양의 window를 사용하는 self-attention은 isotropic(등방성) 특성으로 인해 directional frequency information을 캡쳐하는 데 비효율적이다.

이를 해결하기 위해 논문에서는 네 가지 형태의 window를 병렬로 사용하는 FDWA 모듈을 제안했다.
네 가지 window의 크기 (hxw)는 4s x 4s , s x s, s x 4s, 4s x s로 설정되며, 여기서 s는 window 크기를 나타낸다. 이 window는 각각 저주파, 고주파, 수직, 수평 성분에 해당한다.

2차원 주파수 분해의 관점에서 이러한 구현은 각 차원에서 저주파 & 고주파 분해의 permutation
& combination에 해당한다고 한다. 이 window attentiond은 논문에서 각각 LL-WA, HH-WA, HL-WA, LH-WA로 명명된다.

input hidden representation의 shape은 CxHxW이고 C는 채널 수를 나타낸다. 먼저 이르르 K개의 헤드로 Linear Projection 후 K/4개의 헤드로 이루어진 네 개의 병렬 그룹으로 나누고, 각 그룹은 특정 유형의 self-attention을 수행한다.

논문에서는 LH-WA의 경우를 예로 들어 설명했다.

Example - LH-WA component

입력 X는 4s x s 크기의 window $[X_1, \dots , X_M]$로 균등하게 나뉜다. k번째 헤드에 projection된 Q,K,V가 $d_k$ 차원 텐서랃고 가정할 때, k번째 헤드의 LH-WA 출력은 아래와 같이 계산된다.

다른 세 가지 유형의 window attention에 대해서 동일하게 적용되며, 이들의 출력은 아래와 같이 병합된다.

Frequency-Modulation Feed-Forward Network (FMFFN)

feed-forward network (FFN)은 Transformer 아키텍쳐에서 Self-Attention으로 생성된 Feature를 정제하기 위해 사용된다. 이전에 FDWA를 통해 다양한 주파수 성분을 가진 feature가 생성된다. 그러나 압축에서 주파수 성분의 기여도는 동일하지 않다.
예를들어 high-bitrate models은 edge와 fine-grained details을 복원하기 위해 고주파 성분을 더 많이 필요로 하는 반면, low-bitrate models은 주로 저주파 성분에 의존하여 전체 구조를 복원한다.

본 논문에서는 다양한 주파수 성분을 adaptively modulate하고 성분간의 중복성을 제거하기 위해 Frequency-Modulation FFN (FMFFN)을 제안한다.
FMFFN은 feature를 주파수 도메인으로 변환하여 학습 가능한 필터를 통해 주파수 성분을 선택적으로 증폭하거나 억제한 뒤 다시 공간 도메인으로 변환한다.

FMFFN의 전체 과정은 아래와 같다.
1. 입력 X는 1x1 Conv와 GELU를 통과하여 $X_{ffn}$으로 변환.
2. $X_{ffn}$은 block-based fast Fourier transform (FFT)을 통해 주파수 도메인으로 변환.
3. 학습 가능한 필터 $W$는 주파수 성분을 선택적으로 증폭하거나 억제하기 위해 $X_{ffn}$에 곱해짐.
4. $X_{ffn}$은 inverse FFT (IFFT)을 통해 공간 도메인으로 변환되고 최종 $X_{out}$ 출력

Transformer-Based Channel-Wise Autoregressive (T-CA) Entropy Model

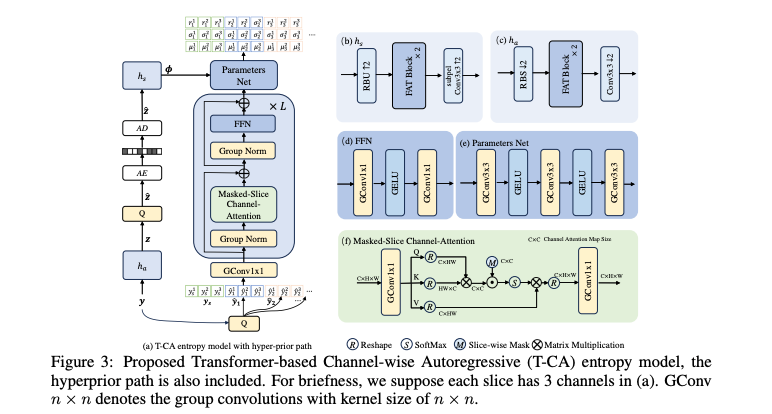
이전의 channel-wise autoregressive models은 잠재표현 $y$를 채널방향으로 여러 슬라이스로 나눈 뒤, 각각의 슬라이스가 이전에 디코딩된 슬라이스에 의존하는 관계를 CNN을 사용해 학습한다. 그러나 입력 이미지에 따라 채널 내 계수의 분포가 크게 달라지기 때문에, CNN에서 고정된 가중치로는 채널 간의 상관관계를 충분히 활용하지 못하는 문제가 있다.

본 논문에서는 transformerbased channel-wise autoregressive (T-CA) entropy model를 제안했고, 이는 채널 및 슬라이스 간의 종속성을 효과적으로 학습하여 더 정밀한 분포 추정을 가능하게 한다고 한다.

T-CA는 Vision Transformer과 유사한 구조의 L개의 Transformer Layer로 구성된다. 하지만 spatial attention 대신 channel attention을 사용한다.

양자화된 MxHxW $\hat{y}$ 잠재표현에서 이를 n개의 슬라이스로 나누며, 각 슬라이스는 균등하게 나눠진다.

Transformer에 들어가기전에 각 슬라이스는 $r\cdot M_s$ ($M_s=M/n_s$)개의 채널로 Projection되며, 이는 Group Convolution을 통해 구현된다. 이 때 입력채널과 출력 채널은 각각 M과 $r\cdot M$이며 커널 크기는 1x1, 그룹 수 $n_g$는 $n_s$ 즉 슬라이스 개수와 동일하다.

본 논문에서는 Transformer 구조를 그대로 사용하는 것이 아닌 약간의 수정사항이 있다.
첫 번째로 causal slice-wise mask를 통합하여 masked-slice channel attention을 도입했다. 이를 통해 아직 인코딩되지 않은 슬라이스가 다른 슬라이스에 영향을 미치지 않도록 한다.
두 번째로 LayerNorm을 GroupNorm으로 대체하고 모든 Linear 층을 1x1 Group Conv로 대체했으며 그룹 수는 앞서 언급한 슬라이스 수를 사용했다. 이러한 그룹 기반 연산은 슬라이스 내 채널 종속성을 모델링하는 데 유리하고, 모델 복잡도를 줄여 계산 효율성을 향상시킨다고 한다.

Experiments

데이터셋은 Flickr2W, ImageNet-1k를 사용했으며, 평가는 Kodak (768×512) 24장, Tecnick (1200x1200) 100장 , CLIC Professional Validation (2K) 41장을 사용했다고 한다.

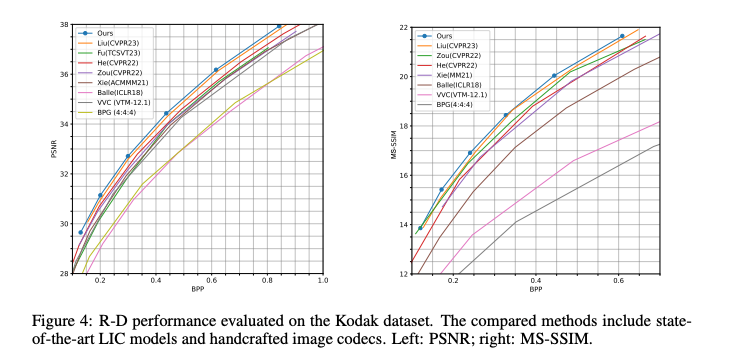
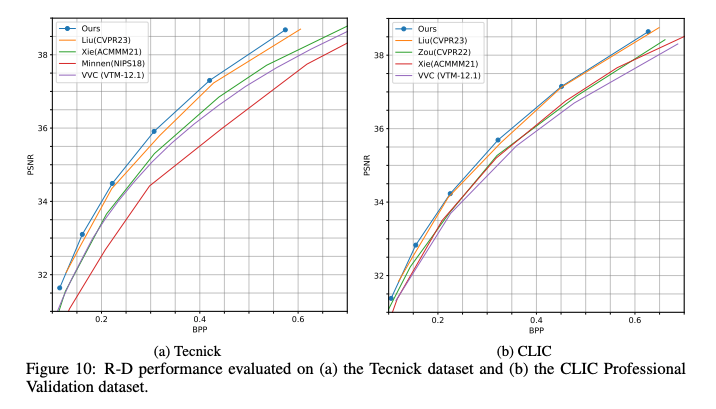
결과를 살펴보면 세 데이터셋에서 모두 우수한 성능을 보였다.

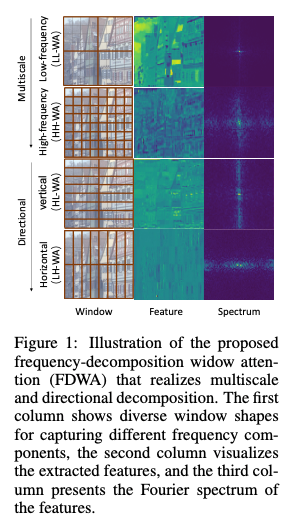
Spectrum analysis of FDWA

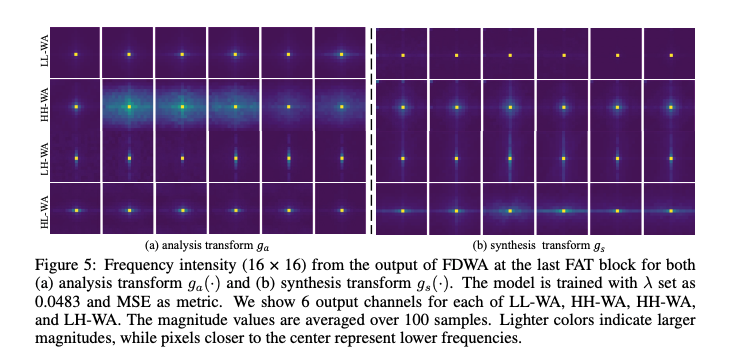
FDWA에서 Attention 모듈에서 출력 feature map에 FFT를 적용하여 주파수 성분의 강도를 시각화한 이미지이다.
이미지를 살펴보면 HH-WA가 더 많은 고주파를 포착하며, LL-WA는 주로 저주파에 집중한다는 것을 명확히 보여준다.
또한, HL-WA와 LH-WA는 방향성 주파수를 포착하는 능력을 보여줬다.

Visualization analysis of FMFFN

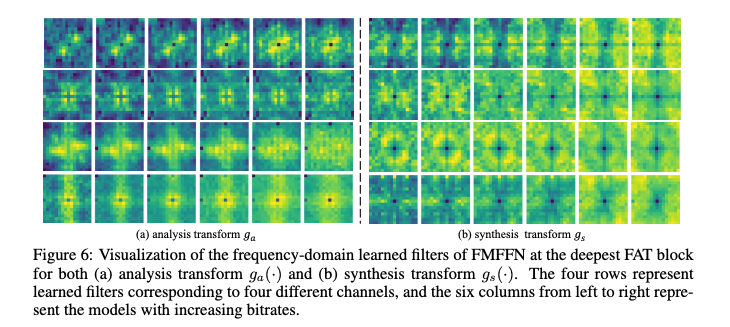
FMFFN의 주파수 도메인 학습 필터 𝑊를 시각화한 이미지이다. 각 행에서 왼쪽에서 오른쪽으로, 6개 열은 다른 bit-rate를 가진 모델의 필터를 나타낸다. 더 높은 bit-rate의 모델이 더 많은 고주파 성분을 포함한다는 것을 알 수 있다.

Conclusion

• 제안된 FTIC는 Frequency-Decomposed Window Attention(FDWA)와 Frequency-Modulation Feed-Forward Network(FMFFN)를 도입하여 방향 및 공간 주파수 성분을 포착.
• 또한 Transformer based Channel-wise Autoregressive (T-CA) entropy model을 설계하여 channel dependencies를 더 효과적으로 학습.