[Week 1] Convex sets [2]

4. Generalized inequalities

이번에는 $n$차원 벡터의 크기를 비교하기 위한 generalized inequality에 대해 알아보자.
cone $K \in R^n$이 다음 성질들을 만족하면 proper cone이라고 부른다.

1. k is convex.
2. k is closed. (경계를 포함하는 집합)
3. k is solid. (interior is not empty)
4. k is pointed (직선을 포함하지 않는다.)

---

*3에 대한 설명: 다음 두 집합을 살펴보자.

$C_1 = \{(x_1, x_2) | x_1 \geq 0, x_2=0\}$

$C_2 = \{(x_1,x_2)|x_1,x_2 \geq 0\}$

다음 두 집합은 모두 closed convex cone이다. 그러나 $C_2$만 solid하다. 왜냐하면 $C_1$의 모든 점은 모두 $C_1$의 경계면에 위치해 있고, 따라서 interior가 없다.

---

이 proper cone은 generalized inequality를 정의할 때 사용된다. $\mathbb{R}^n$상의 점 $x,\, y$에 대하여 generalized inequality는 다음과 같의 정의된다.

$x \preceq_K y \iff y-x \in K\\x\prec_K y \iff y-x \in \textbf{int}\,K$

만약 $K = \mathbb{R_+}$일 경우 generalized inequality와 $\mathbb{R}$에서의 inequality $\leq$ 는 같다.

여기에 대해서 성립하는 몇 가지 성질들은 다음과 같다.

• preserved under addition: if $x \preceq_K y$ and $u \preceq_K v$, then $x+u \preceq_K y+v$.
• transitive: if $x \preceq_K y$ and $y \preceq_K z$ then $x \preceq_K z$.
• preserved under nonnegative scaling: if $x \preceq_K y$ and $\alpha \geq 0$ then
  $\alpha x \preceq_K \alpha y$.
• reflexive: $x \preceq_K x$.
• antisymmetric: if $x \preceq_K y$ and $y \preceq_K x$, then $x=y$.
• preserved under limits: if $x_i \preceq_K y_i$ for $i = 1,2,…,$ $x_i \rightarrow x$ and $y_i \rightarrow y$
  as $i \rightarrow \infty$, then $x \preceq_K y$.

등호가 없는 경우에는 아래와 같다.

• if $x \preceq_K y$ then $x \prec_K y$.
• if $x \prec_K y$ and $u \preceq_K v$, then $x+u \prec_K y+v$.
• if $x \prec_K y$ and $\alpha > 0$ then $\alpha x \prec_K \alpha y$.
• $x \nprec_K x$.
• if $x \prec_K y$ and for $u,\,v$ small enough, $x + u \prec_K y + v$

generalized inequality의 성질은 $\leq$와 비슷하지만 다른 점이 있다. 가령 $\leq$는 linear ordering으로, 임의의 두 원소에 대하여 항상 inequality를 정의할 수 있지만 이것이 성립하지 않을 수 있다. 여기서 maximum과 minimum의 개념이 기존보다 조금 복잡해진다.

어떤 집합 $S$의 원소 $x$가 모든 다른 원소 $y$에 대해 $x \preceq_K y$ 를 만족하면 이 $x$는 $S$의 minimum이라고 부른다. 따라서 $x$는 다른 원소들과 비교 가능하며 같거나 크다. 수식으로 표현하면 다음과 같다.

비슷한 개념으로 minimal이 있는데, 어떤 집합 S의 원소 $x$에 대해 $y \preceq_K x$인 경우는 $x=y$인 경우 뿐이다. nothing is smaller라고 표현하면 적합할 것 같다. 수식으로 표현하면 다음과 같다.

가령 아래 그림에서 $x_1$은 $\mathbb{R}^2_+$에서 정의된 inequality에 대하여 minimum, $x_2$는 minimal point이다.

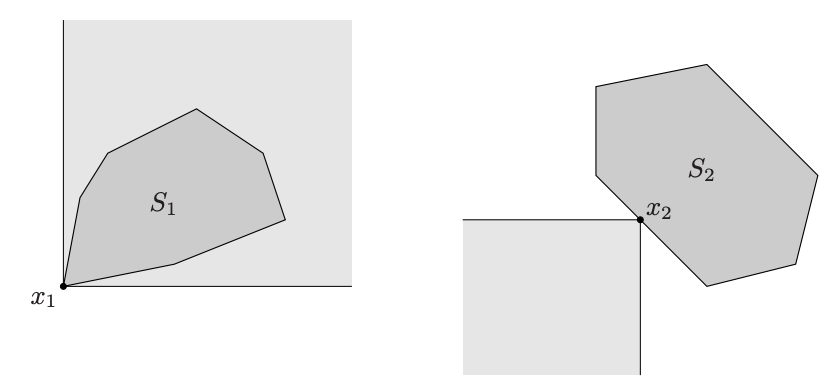
또다른 예로, ordering $\{1,2,3,…,\}$에서 $1$은 minimum element이다. 만약, $2$부터 시작하는 자연수에 ‘나눌 수 있음’으로 순서를 부여했다고 해 보자. 따라서 $a \leq b$는 $a$로 $b$를 나눌 수 있다는 것이다. 그러면 minimal elements는 소수가 된다. 그렇지만 minimum은 아니다.

5. separating and supporting hyperplanes

다음 두 theorem은 $\mathbb{R}^n$상에서 convex set의 위치를 정확하게 정한다는 의의를 지니고 있다.

Separating hyperplane theorem

어떤 두 convex set $C$와 $D$가 disjoint일 때, 그 두 집합은 어떤 hyperplane $a^Tx = b$로 구분될 수 있다. 즉 하나는 한쪽 halfspace, 다른 것은 반대쪽에 속한다. (역은 성립하지 않을 수 있다.) 머신러닝의 관점에서, 어떤 데이터가 convex하게 분포되어 있으면 linearly seperable하다.

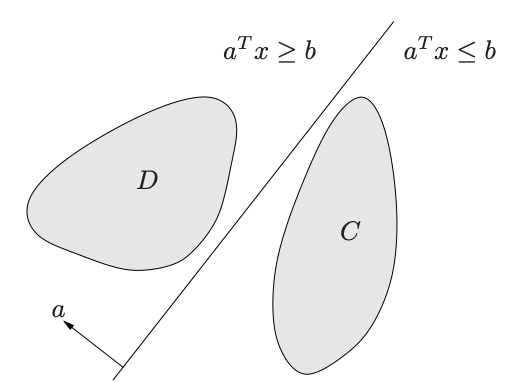
이때 등호가 없는 separation이 성립할 수도 있는데, (i.e. C in $a^Tx > b$, D in $a^Tx < b$) 밑의 그림처럼 항상 가능하지는 않다.

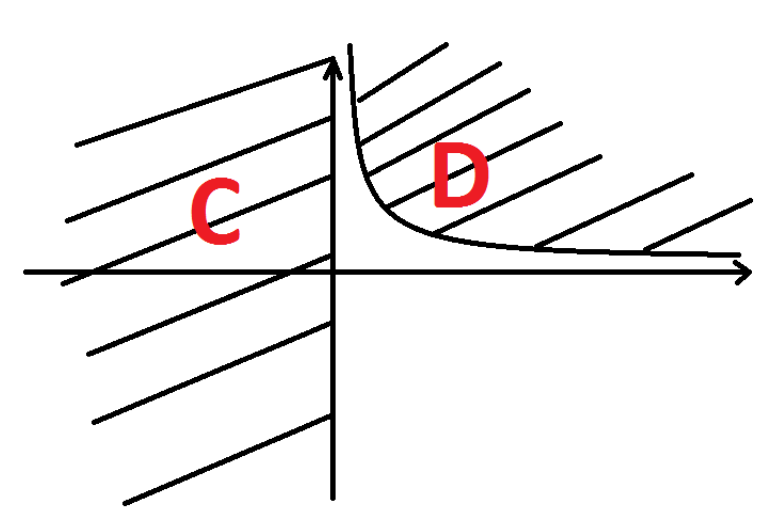
그렇지만 중요한 건 결국 등호가 없는 경우의 strict한 separation이다. 이 경우는 아래와 같다.

Let $C$ and $D$ be closed convex sets in $R^n$ with at least one of them bounded, and assume that $C \cap D = \emptyset.$ Then $\exists a \in \mathbb{R}^n,\,a\ne 0,\, b\in \mathbb{R}\,\,s.t.$
$a^Tx >b,\,\,\forall x \in D$ and $a^Tx <b,\,\,\forall x \in C$

Proof.
두 convex set의 거리를

와 같이 정의하자.
$c \in C$ 와 $d \in D$를 이 infimum에 해당하는 점이라고 하자. 그 다음,

위와 같이 seperating hyperplane$f(x) = a^Tx - b$의 파라메터를 정의하자. 그러면 우리의 주장(claim)은

가 된다.
$a, b$를 이렇게 선택한 이유는 아래에서 볼 수 있듯 hyperplane이 $c, d$ 사이를 반 가르게 선택하기 위해서이다.

이제 모든 $x \in D$에 대해$f(x) > 0$임을 증명하면 반대의 경우는 대칭적이므로 증명이 끝난다.

모순을 이끌어내기 위해, $f(\bar{d}) \leq 0$인 $\bar{d} \in D$가 존재한다고 가정하자. 그러면

이어야 한다.

이제 $g(x) = \|x - c\|^2$를 정의하자. 그러면 $\bar{d} - d$는 $d$로부터 $g$에 대해 descent direction이 된다. 정확한 수식적 유도는 아래와 같다.

이 때 첫 번째 부등식은 $(1)$로부터 나왔고, 두 번째 부등식은 $d \neq c$로부터 알 수 있다.

따라서 다음 사실이 성립한다.

하지만 이것은 $d$ 가 $c$와 가장 가까운 점이라는 사실에 모순이므로 우리가 가정한 $\bar{d}$는 존재하지 않는다.

중요한 따름정리는 다음과 같다.

Let $C$ be a closed convex set and $x_0 \notin C$. Then there exists a hyperplane that strictly separates from $C$.

여기에서 Farkas’ Lemma라는 매우 중요한 정리가 나오고, 이 보조정리에서 LP strong duality 성질이 유도되는 구조이다. 이 내용은 나중에 다루도록 하자.

Supporting hyperplane theorem

어떤 집합이 supporting hyperplane을 갖는다는 것은 그 집합이 hyperplane을 통해 분리된 halfspace 중 하나에 온전히 속하며, hyperplane과 접하는 경계점이 적어도 하나 존재한다는 것이다.

구체적으로, 집합 $S \subseteq \mathbb{R}^n$의 경계점 $x_0 \in \text{bd}\,S = \text{cl}\,S \backslash \text{int}\,S$와 $a\neq 0$에 대해 $a^Tx \leq a^Tx_0\,\,\forall x\in S$를 만족하면 hyperplane $\{x\,|\,a^Tx = a^Tx_0\}$를 $S$의 supporting hyperplane이라 한다.

따라서 halfspace $\{x\,|\,a^T(x_0-x) \geq 0\}$(normal vector의 반대쪽)이 집합을 포함하게 된다.

convex set의 경우 경계면의 점 $x_0$와 접하는 supporting hyperplane이 적어도 하나 존재한다.

반대로, 만약 $S$가 interior를 가지는 closed nonempty set이고 모든 경계면의 점이 그 점을 포함하는 supporting hyperplane을 가질 경우, $S$는 convex set이며 모든 supporting hyperplane의 교집합 역시 convex set이다.

결국 이것은 임의의 convex set의 공간상의 위치를 supporting hyperplane이 이루는 halfspace의 교집합으로 정확히 나타낼 수 있다는 말이므로, 두 hyperplane theorem은 궁극적으로 같은 뜻이다.

6. Dual cones and generalized inequalities

쌍대공간(Dual space)는 어떤 벡터공간 $V$에서 정의된 모든 linear form, 즉 스칼라로 맵핑되는 선형함수를 모은 공간이다. 우리 세션에서는 자세한 수학적 논의는 하지 않고 교재에 소개된 내용만 살펴보았다.

Dual cones

Cone $K$의 dual cone $K^*$는 다음과 같이 정의된다.

이름 그대로 $K^*$는 cone이며, 원래 $K$에 상관없이 항상 convex set이다. 기하적으로, $y\in K^*$ 는 $-y$가 $K$의 원점에서의 supporting hyperplane의 normal vector임과 동치이다.

(사실 위 그림처럼, dual cone은 원래 set이 cone이 아니어도 cone이다.)

예시로, positive semidefinite cone $\mathbb{S}^n_+$은 자기가 자기 자신의 dual cone인 self-dual이다. 따라서 $n \times n$ square matrix $Y$에 대하여

임이 성립한다. 이 사실을 증명해 보자. 만일 $Y \notin \mathbb{S}^n_+$라면, $q^TY q = \text{tr}(qq^TY) <0$인 $q$가 존재하고 따라서 positive semidefinite인 $X = qq^T$에 대한 반례가 생겨 $Y$는 $X$의 dual cone에 속하지 않는다. 반대로 $Y \in \mathbb{S}^n_+$라면 positive semidefinite인 $X$의 eigen decomposition $X = \sum_{i=1}^n \lambda_i q_i q_i^T$를 정의했을 때 모든 eigenvalue가 $0$보다 크거나 같으므로 $\text{tr}(YX) = \text{tr}\left(Y \sum_{i=1}^n \lambda_i q_i q_i^T\right) = \sum_{i=1}^n \lambda_iq_i^TYq_i \geq 0$이다. 따라서 $(\mathbb{S}^n_+)^* = \mathbb{S}^n_+$이다.

만일 원래의 cone $K$가 proper cone이면 dual cone도 proper cone이며, $K^{**} = K$이다. 즉 dual cone 상에서도 inequality를 정의할 수 있는데, 다음 문단에서 살펴보자.

Dual generalized inequalities

방금 말했듯 원래 cone이 proper cone이면 dual cone에서도 inequality가 정의되는데, 둘은 상호작용하는 성질이 있다. 아래 두 개는 매우 중요한 성질이며, $K$와 $K^{*}$를 서로 바꿔도 동일하게 성립한다.

• $x \preceq_K y \iff \lambda^T x \leq \lambda^T y\,\,\text{for all}\,\,\lambda \succeq_{K^*} 0$.
• $x \prec_K y \iff \lambda^T x < \lambda^T y\,\,\text{for all}\,\, \lambda \succeq_{K^*} 0, \lambda \neq 0$

이 성질을 통해 dual cone을 이용하면 기존의 벡터에 대한 inequality를 스칼라에 대한 inequality로 훨씬 간단하게 표현할 수 있음을 알 수 있다.

Minimum and minimal elements via dual inequalities

이제 마지막이자 섹션 6의 의의가 되는 부분으로, $\mathbb{R}^m$상의 set의 minimum / minimal element를 dual inequality를 이용해 표현해 보자.

proper cone $K$에서 정의된 generalized inequality 기준, 집합 $S$의 minimum element의 정의는 다음과 같이 dual cone을 이용하여 표현할 수 있다.

$x$ is the minimum element of $S$, with respect to the generalized inequality $\preceq_K$, if and only if for all $\lambda \succ_{K^*} 0$, $x$ is the unique minimizer of $\lambda^Tz$ over $z \in S$.

기하적으로 이는 아래 그림처럼 $S$의 supporting hyperplane $\{z\,|\,\lambda^T (z-x) = 0 \}$이 $x$를 유일한 접점으로 가짐을 말한다.

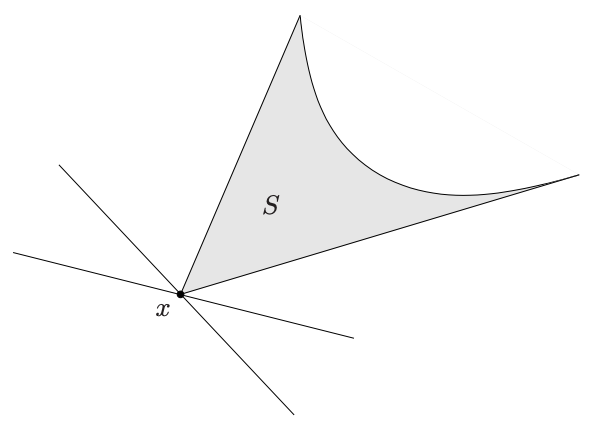
이제 miminal element에 대해 살펴보자. $S$의 minimal element는 다음과 같이 표현할 수 있다.

If $\lambda \succ_{K^∗} 0$ and $x$ minimizes $\lambda^Tz$ over $z \in S$, then $x$ is minimal.

이 정의에는 미묘한 점이 있다. 먼저 이 명제는 양방향이 아님에 주의하자. 아래 그림에서 $x$는 $S$의 $\mathbb{R}^2_+$상의 minimal element지만, 접선을 그을 수 있는 적절한 $\lambda \succ 0$을 찾을 수 없다.

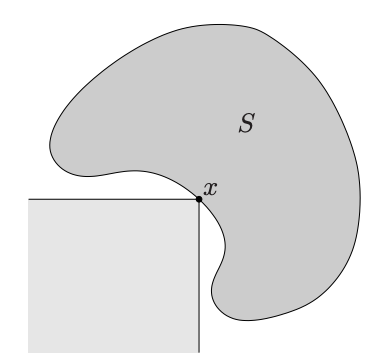
반대 방향은 $S$가 convex set일 때 제한적으로 성립한다. 만일 $S$가 convex set이고 $x$가 minimal element라면, $x$는 임의의 $\lambda \succeq_{K^*}0$에 대해 $\lambda^Tz$의 minimizer이다. (다만 $\succ_{K^*}$에 대해서는 성립하지 않을 수 있다.) 따라서 convexity 조건이 있어야만 벡터 최적화 문제를 이 방식으로 풀 때 가능한 전체 해를 탐색할 수 있다.

아래 그림은 이런 벡터 최적화 문제의 적용 예시이다. 연료와 노동력을 투입해 최대 효율을 달성하고 싶을 때, 같은 생산량을 도출하는 자원 벡터들의 다양한 조합(생산 방법)은 $P$와 같다. 우리의 목표는 $P$의 minimal element인, 가장 자원을 적게 소모하는 조합 벡터를 찾는 것이고 이 기준은 componentwise inequality이다. 가령 $x \preceq y$라는 것은 두 벡터의 각 원소 모두에 대해 각각 $x_i \leq y_i$라는 뜻이다. 이때 minimal element, 즉 더 개선할 필요가 없는 상태를 pareto optimal이라고 한다. 이때 $\lambda \succeq 0$을 각각의 자원 투입에 대한 비용(cost)으로 생각해 $\lambda^Tx$를 최소화하는 문제로 표현하는 것은 이 문제를 푸는 효과적인 접근 방식이다.

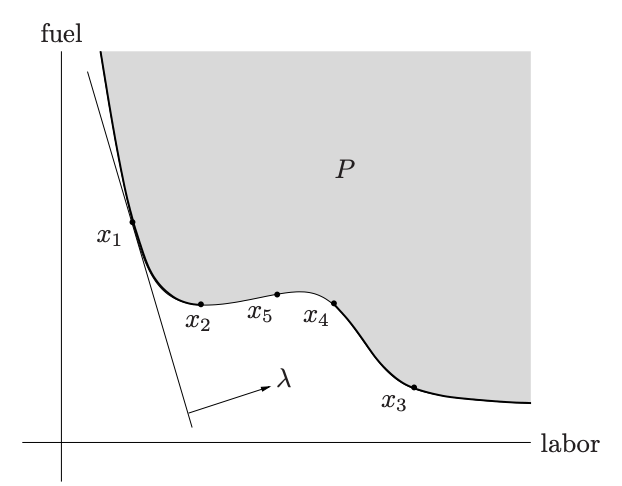
위 그림에서 $x_5, x_4$는 둘다 $x_2$에 밀리므로 효율적인 솔루션이 아니다. $x_1, x_3$은 $\lambda^Tx$의 최소화 문제를 통해 찾을 수 있는 솔루션이다. 반면 $x_2$는 minimal element이지만 이 방법으로 찾을 수 없다.