[Week 1] Statistical estimation [1]

*세션 교재: Convex optimization - Boyd and Vandenberghe Ch.7.

봄학기 첫 세션에서는 우리가 전공에서 배운 다양한 통계적 기법들이 최적화 문제로서 어떻게 표현될 수 있는지 살펴보았다.

1. Parametric distribution estimation

Optimization variable $x\in \mathbb{R}^n$이 density가 $p(\cdot)$인 확률분포의 parameter라고 하자. 데이터 $y$가 주어졌을 때, maximum likelihood(ML) estimation 은 주어진 데이터에서 likelihood function $p(y|x)$를 최대화하는 $x$를 추정하는 문제이다. 주로 계산의 편의상 log likelihood를 이용하는 것 역시 익숙할 것이다. 이때 여러 알려진 분포 가정 하에서는 log likelihood가 데이터 $y$에서 $x$에 대한 concave function일 때가 많으므로, $x$의 범위에 관한 prior knowledge, 즉 제약식이 convex이면 ML estimation은 컨벡스 최적화 문제가 된다. 그 일반적인 형태는 아래와 같을 것이다. 만일 $m$개의 데이터가 iid로 추출되었다고 가정한다면 likelihood function은 $\prod_{i=1}^m p(y|x)$또는 $\sum_{i=1}^m \log p(y|x)$의 형태가 된다.

$\text{maximize}\,\,l(x) = \log p(y|x)$
$\text{subject to}\,\,x \in C$

예시를 통해 차근차근 살펴보자.

Example 1. Linear measurement

첫 번째 예시는 우리가 익히 잘 아는 문제이다.
$y_i = a_i^Tx + v_i,\,\,\,\,v_i \overset{iid}{\sim}(\mu,\sigma^2)$
으로, $m$개의 데이터 $a_i$와 $y_i$의 관계를 설명하는 선형 회귀식의 계수 $x \in \mathbb{R}^n$를 찾는 회귀분석 문제이다. Density가 $p$인 $v_i$에 대한 log likelihood function은
$l(x) = \sum_{i=1}^m p(y_i-a_i^Tx)$이다.

1. Gaussian noise
$v_i \overset{iid}{\sim} N(0,\sigma^2)$일 때 log likelihood function은 $-\frac{m}{2} \log(2\pi \sigma^2) - \frac{1}{2\sigma^2}||Ax-y||_2^2$ 이다. (이때 $A$는 각 행이 $a_i^T$인 $m \times n$ 행렬이다.)
따라서 $\hat{x}_{mle} = \argmin_x ||Ax-y||_2^2$로 OLS estimator와 동일하다.

2. Laplacian noise
$v_i$가 평균이 0인 라플라스 분포를 따를 때, $p(z) = (1/2a)e^{-|z|/a}(a>0)$이므로 $\hat{x}_{mle} = \argmin_x ||Ax-y||_1$이다.

3. Uniform noise
$v_i$가 $[-a, a]$에서 정의된 균일분포를 따를 때, $p(z) = 1/2a$이고 $\hat{x}_{mle}$는 $||Ax-y||_{\infty} \leq a$를 만족하는 임의의 값이 될 수 있다.

2번과 같은 l1 norm approximation은 l2 norm의 경우보다 더 robust하다. 왜냐하면 라플라스 분포는 정규분포보다 heavy-tail을 갖고 있고, 따라서 큰 절댓값의 noise가 발생할 확률이 좀 더 높게 측정되므로 이상치에 덜 민감하게 된다.

Example 2. Generalized linear model

Linear model은 $E(y|A) = Ax$의 형태로 모델링한 것으로 $A$에 대한 $y$의 conditional expectation이 선형으로 변한다는 것이다. Generalized linear model(GLM)은 conditional expectation 자체가 아닌 그것에 어떤 함수 $g$를 취한 것이 선형으로 변한다고 가정한 모델로, $y$가 실수 전체에서 정의되는 연속형 변수가 아닐 때 사용할 수 있다. 많이 사용되는 GLM에는 poisson model과 Bernoulli model이 있다.

1. Poisson model
가령 $y$가 '방문객의 수'와 같은 양수인 정수로만 정의되는 변수일 경우 이것을 linear model로 나타내는 것은 비합리적이다. Poisson model의 가정은 아래와 같다.
$\mathbb{P}(y|A) = \frac{\mu^y e^{-\mu}}{y!},\,\mu = e^{Ax}$

따라서 이 모델은 $\log E(y|A)$가 선형으로, 즉 $E(y|A)$가 배수로 변한다고 가정한 것이다. Log likelihood function은
$l(x) = \sum_{i=1}^m y_i a_i^Tx - \exp(a_i^Tx) - \log(y_i!)$가 되고, 이를 최대화하는 $x$값을 찾는 것이 목표가 된다.

2. Logistic model
이번에는 $y|A \sim Bernoulli(\mu),\,\,\mu=\frac{1}{1+e^{-Ax}}$라고 가정해 보자. 가령 $y$가 '질병 여부'와 같은 yes or no 여부만 중요한 변수일 경우이다. 이 모델은 log odds $log\left(\frac{\mu}{1-\mu}\right) = Ax$라고 가정한 것으로, 변수가 yes(1)일 경우의 상대적인 가능성을 나타내는 odds가 배수로 변한다고 정의한 것이다. 베르누이 분포에 대한 Likelihood function은
$L(x) = \prod_{i=1}^m \mu_i^{y_i}(1-\mu_i)^{1-y_i}$이므로 log likelihood function은
$l(x) = \sum_{i=1}^m y_i \log(\mu_i) + (1-y_i)\log(1-\mu_i)$이다.

이 두 문제는 $x$에 대한 컨벡스 최적화 문제로서 풀 수 있다.

Maximum a posteriori probability estimation

MAP estimation은 MLE의 베이지안 버전으로, parameter $x$를 random variable로 보는 관점이다. 여기에서는 $x$와 데이터 $y$가 joint density $p(x,y)$를 따른다고 가정하고, $x$의 prior density를 $p(x) = \displaystyle \int p(x,y) dy$로 정의한다. 그리고 estimation의 목표는 $x$의 posterior probability $p(x|y)$를 최대화하는 estimator를 도출하는 것이다. 베이즈 정리에 의해 $p(x|y) = \frac{p(x,y)}{p_y(y)} = p(y|x)\frac{p(x)}{p(y)}$이고 분모의 $p(y)$는 normalizing constant이기 때문에 결국 원하는 것은 분자를 최대화하는 $x$값을 찾는 것이다. 결국 MLE와 다른 것은 $x$에 대한 prior density가 추가되었다는 것 뿐이다. 로그를 취하면 $x$에 대한 MAP estimator는 다음과 같이 나타낼 수 있다.

$\hat{x}_{map} = \argmax_x (\log p(y|x) + \log p(x))$

최적화 문제 관점에서 이 문제는 mle를 찾는 문제에 $x$를 제한하는 term(작은 prior probability를 가진 값을 무시)을 추가한 것과 같다. 그리고 $x \in C$에서 log-concave한 prior density를 사용하면 이 문제 역시 컨벡스 최적화 문제가 될 수 있다.

Example. Linear measurement

위 예시의 베이지안 버전을 살펴보자.
$y_i = a_i^Tx + v_i,\,\,\,\,v_i \overset{iid}{\sim}(\mu,\sigma^2)$
에서 $x$가 prior density $p_x(x)$를 가졌다고 생각하면 posterior density는
$\log p_x(x) + \sum_{i=1}^m p_v(y_i-a_i^Tx)$
이다. 예시로, $v$가 $[-a,a]$에서의 uniform noise이고 $x \sim N_n(\mu, \Sigma)$라면 이 문제는 $x$에 대한 QP가 된다.

$\text{minimize}\,\,(x-\mu)^T \Sigma^{-1} (x-\mu)$
$\text{subject to}\,\,||Ax-y||_\infty \leq a$

2. Nonparametric distribution estimation

이번에는 분포의 파라메터가 주어져 있지 않고, 단지 확률변수 $X$가 finite set $\{\alpha_1,\,...,\,\alpha_n\} \subseteq \mathbb{R}$의 값을 가진다고 하자. 그러면 $X$의 distribution은 $\{p\in \mathbb{R}^n\,|\,p \succeq 0,\,1^Tp = 1 \},\,\,\mathbb{P}(X=\alpha_k) = p_k$로 나타낼 수 있다. 이번에는 이 distribution $p$를 추정하는 방법에 대해 알아보자.

Prior information

$p$에 대해 우리가 가진 여러 사전 정보들은 convex constraint로 표현할 수 있는 것들이 많다.
임의의 $f:\mathbb{R} \rightarrow \mathbb{R}$에 대하여 $Ef(X) = \sum_{i=1}^n p_if(\alpha_i)$이고 이것은 $p$에 대한 linear function이다. 특수한 경우로 아래처럼 indicator function의 expected value는 확률과 같음을 기억하자.
$\mathbb{P}(X \in C) = c^Tp,\,\,\,\,c_i=\begin{cases} 1\,\,\,\,\alpha_i \in C\\ 0 \,\,\,\,\alpha_i \notin C \end{cases}$

이와 같이 $X$의 moment 또는 확률에 대한 제약 조건 역시도 아래처럼 $p$에 대한 linear function으로 나타낼 수 있다.
$E(X) = \sum_{i=1}^n \alpha_ip_i = \alpha$
$E(X^2) = \sum_{i=1}^n \alpha_i^2p_i = \beta$
$\mathbb{P}(X \geq 0) =\sum_{\alpha_i \geq 0} p_i \leq 0.?$

$Var(X) = E(X^2) - E(X)^2$ 역시도 앞의 항은 linear, 뒤의 항은 concave quadratic이므로 $p$에 대한 concave function이다. 다른 예시로, conditional probability에 대한 조건 $P(X \in A\,|X \in B)$ 역시 $\alpha_i \in A \cap B$와 $\alpha_i \in B$에 대한 indicator function $a,\,b$를 각각 정의하면 $a^Tp/b^Tp$의 linear-fractional function으로 나타낼 수 있다.

Solving problems

이런 $p$에 대한 사전 정보는 최적화 문제의 제약 조건 $p \in \mathcal{P}$라고 일반화될 수 있다. 문제의 objective로 많이 쓰이는 것들은 아래의 예시와 같다.

1. Expected value(min or max)
$\sum_{i=1}^n f(\alpha_i)p_i$

2. Log likelihood(max)
$N$개의 iid samples $x_1,\,...,x_N$이 주어졌을 때, $k_i$를 $x = \alpha_i$인 샘플 갯수라고 정의하자. 그러면 $k_1 + \cdots k_n = N$이고, log likelihood function은 아래처럼 표현된다.
$\sum_{i=1}^n k_i \log p_i$

3. Entropy(max)
가장 정보량이 많은 분포 $p$를 찾기 위한 objective이다. 균등하게 분포할수록 불확실성이 크므로 엔트로피도 커진다.
$-\sum_{i=1}^n p_i \log p_i$

4. KL divergence(min)
어떤 분포 $q$와 가장 가까운 $p$를 찾기 위한 objective이다.
$\sum_{i=1}^n p_i \log (p_i/q_i)$

만일 $q = (1/n)\mathbf{1}$이라면 이 문제는 maximum entropy 문제와 동일해진다.

3. Optimal detector design and hypothesis testing

이번에는 확률변수 $X$가 $\{1,\,2,\,...,\,n\}$의 값을 가지고, 그 분포의 파라메터 $\theta$의 값이 $\{1,\,2,\,...,\,m\}$중 하나라고 하자. 그러면 각 $\theta$값에 따른 $X$의 확률분포는 각각의 원소가 아래와 같은 $n \times m$ 행렬 $P$로 표현될 수 있다.

$p_{kj} = \mathbb{P}(X=k\,|\,\theta = j)$

이때 $X$의 observation을 가지고, 올바른 분포의 parameter $\theta$를 추정하는 것을 hypothesis testing 또는 detecting이라고 한다. 이때 $\theta$에 대한 추정치 또는 detector $\hat{\theta}$는 단순히 맞고 틀린지 여부만 중요할 수도 있고, 실제 값에 얼마나 가까운지가 중요할 수도 있다. 또 가능한 $X$나 $\theta$값의 집합은 실제 값이 아닌 index set으로만 볼 수도 있고, 연속된 실수 값(uncountable set)일 수도 있음에 유의하자.
(i.e. $\theta \in \{\theta_1,\,...,\,\theta_m\}\,\,\text{or}\,\, \theta \in [\theta_1, \theta_m]$)

Deterministic and randomized detectors

Detector를 observation $k$에 대해 정해진 값으로 사용하는 것을 deterministic detector라고 한다. 가령 mle는 observation $k \in \{1,\,...,\,n\}$에 대해 $\psi(k) =\argmax_j p_{kj}$이므로 deterministic detector이다. Randomized detector $\hat{\theta} \in \{1,\,...,\,m\}$는 observation $k$에 대해 일정 확률로 선택되는 detector를 말한다. 당연히 randomized decector의 확률분포 역시 아래와 같은 probability matrix $T \in \mathbb{R}^{m \times n}$으로 정의될 수 있다.
$t_{ik} = \mathbb{P}(\hat{\theta}=i\,|\,X=k)$
그러면 $T$의 각 열은 observation $k$에 대한 $\hat{\theta}$의 분포가 된다. 물론 언뜻 보기에는 randomized detector를 굳이 사용할 필요가 없을 것 같다. 왜냐하면 mle와 같은 deterministic detector는 observation을 보고 가장 합리적인 판단을 내리는 것으로 보이기 때문이다. 그렇지만 randomized detector가 더 나은 성능을 보일 때가 있기 때문에, 실제로 가장 합리적인 판단은 우리의 직관과 다를 수 있다. 우리의 목표는 가장 좋은 성능의 확률분포 행렬 $T$를 디자인하는 것이다. 물론 probability matrix이므로 모든 원소는 0보다 커야 하며 각 열의 합은 1이어야 한다.

Detection probability matrix

$T$로 정의된 randomized detector에 대하여, detection probability matrix $D=TP \in \mathbb{R}^{m \times m}$를 다음과 같이 정의할 수 있다.

$D_{ij} = (TP)_{ij} = \mathbb{P}(\hat{\theta} = i\,|\,\theta=j)$

즉 $D_{ij}$는 실제 $\theta$값이 j일때 $\hat{\theta}$ 값을 무엇으로 선택할지에 대한 확률을 나타내고, $D$의 diagonal element $D_{ii} = \mathbb{P}_i^d$는 $\theta=i$일 때 옳은 선택의 확률(detection probability), off-diagonal $\sum_{j \neq i} D_{ji} = \mathbb{P}_i^e$는 오류의 확률(error probability)을 나타낸다. $D$가 identity matrix에 가까울수록 이상적인 상황이다.

Optimal detector design

이제 detector design 문제의 다양한 objective, constraint의 예시에 관해 살펴보자. 떠올릴 수 있는 가장 간단한 예시는 $D_{jj} \geq L_j$나 $D_{ij} \leq U_{ij}$의, variable $T$에 대한 linear inequality 형태의 constraint이다. 추가적인 예시는 아래와 같다.

1. Minimax detector design
$\text{minimize}\,\,\max_{j}\mathbb{P}_j^e$
$\text{subject to}\,\,t_k \succeq 0,\,\,\mathbf{1}^Tt_k = 1,\,\forall k =1,\,...,\,n$

worst-case error probability를 최소화하는 objective로, $t_1,\,...,\,t_n\in \mathbb{R}^m$에 대한 linear programming 문제로 나타낼 수 있다.

2. Bayes decector design
$\text{minimize}\,\,q^T\mathbb{P}^e$
$\text{subject to}\,\,t_k \succeq 0,\,\,\mathbf{1}^Tt_k = 1,\,\forall k =1,\,...,\,n$

가설에 대한 prior probability $q \in \mathbb{R}^m$가 $q_i = \mathbb{P}(\theta=i)$로 주어졌을 때의 objective이다. Error probability의 평균을 최소화하는 문제로도 볼 수 있다.

3. Bias, mean-square error, average absolute error
$\theta$의 크기가 의미 있는, 즉 ordered set인 상황에서는 추정치가 실제 값과 얼마나 먼지를 objective로 할 수 있다. 이런 상황에서는 $\theta \in \{\theta_1,\,...,\,\theta_m\}$이다. 실제 값을 $\theta_i$라고 할 때 Bias는 $\underset{i}{E}(\hat{\theta}-\theta) = \sum_{j=1}^m (\theta_j-\theta_i)D_{ji}$, Mean square error는 $\underset{i}{E}(\hat{\theta}-\theta)^2$, average absolute error는 $\underset{i}{E}|\hat{\theta}-\theta|$ 이며 모두 $D$에 대한 linear(affine) function이다.

Multicriterion formulation and scalarization

이번에는 $D$의 off-diagonal의 각 원소 $D_{ij}$를 최적화 변수로 놓는 상황을 살펴보자. 이 경우는 각 error가 서로 다른 성질을 지녔을 경우에 적합하다. 가령 질병 진단 키트의 민감도(양성을 진단해내는 능력)와 특이도(음성을 진단해내는 능력) 사이에 상충관계가 있을 경우, 최적의 trade-off curve를 찾아내는 것이 좋은 목표가 된다. 이런 문제는 아래와 같이 나타낼 수 있다.

$\text{minimize(w.r.t. } \mathbb{R}_+^{m(m-1)})\,\,D_{ij}$
$i,j =1,\,...,\,m,\,\,i\neq j$
$\text{subject to}\,\,t_k \succeq 0,\,\,\mathbf{1}^Tt_k = 1,\,\forall k =1,\,...,\,n$

앞에서 배웠듯 이 문제는 scalarization 방법으로 풀 수 있었다. Objective끼리의 trade-off 관계를 parameter $\lambda$로 정의하고, $\lambda$에 대한 weighted-sum으로 바꾸어 푸는 것이었다. scalarization을 위해 weight matrix $W(W_{ii} =0,\,W_{ij} > 0)$를 이용해 합으로 나타내면
$\sum_{i,j=1}^m W_{ij}D_{ij} = \textbf{tr}(W^TD)$이고, $\textbf{tr}(W^TD)=\textbf{tr}(W^TTP)=\textbf{tr}(PW^TT)=\sum_{i=1}^n c_k^T t_k$($c_k$는 $WP^T$의 열 벡터)이므로 위의 문제는 아래와 같이 $t_1,\,...,\,t_n$에 대한 n개의 LP로 분리될 수 있다.

$\text{minimize}\,\,c_k^Tt_k$
$\text{subject to}\,\,t_k \succeq 0,\,\,\mathbf{1}^Tt_k = 1$

이 문제의 deterministic한 답은 $c_{kq} =\argmin_j c_{kj}$에 대해 $t_k^* = e_q$임을 알 수 있다. 이는 piecewise-linear인 파레토 경계의 꼭짓점을 나타낸다.

Binary hypothesis testing

이해를 돕기 위해 $m=2$인 경우의 예시를 살펴보자. 가설 두 개 중 어느 것이 옳은지 검정하는 것으로, 우리가 잘 아는 귀무 가설과 대립 가설을 예시로 들 수 있다. 가설 1에서의 데이터 $X$의 분포를 $p=(p_1,\,...,\,p_n)$이라고 하고, 가설 2에서의 분포를 $q=(q_1,\,...,\,q_n)$이라고 하자. 가설 2를 질병 양성과 같이 일반적이지 않은(검증하고 싶은) 상황이라고 하면 흔히 가설 2를 positive로 지칭한다. 그러면 objective인 detector $T \in \mathbb{R}^{2 \times n}$은 $X=k$가 관측되었을 때 $t_{1k}\,\,\text{or}\,\,t_{2k}$의 확률로 가설 1 또는 가설 2를 선택하게 되고 만일 $t_{ik}$가 0 또는 1이면 deterministic detector가 된다. 이제 detection probability matrix를 살펴보자. $D = [Tp \,\,\,\, Tq] = \begin{bmatrix} 1-\mathbb{P}_{fp} & \mathbb{P}_{fn} \\ \mathbb{P}_{fp} & 1-\mathbb{P}_{fn} \end{bmatrix}$로 나타낼 수 있고 이를 confusion matrix라고도 한다. Off-diagonal entry는 잘못된 결정을 말하고, $\mathbb{P}_{fp}$는 false positive, 즉 가설 1이 참인데 가설 2를 선택하는 경우이고 $\mathbb{P}_{fn}$은 false negative를 뜻한다. 이 둘을 모두 최소화하는 문제를 objective로 삼아 최적의 $T$를 디자인해 보자.
Scarlarization한 문제 표현은 아래와 같다.

$\text{minimize}\,\,(Tp)_2 + \lambda (Tq)_1$
$\text{subject to}\,\,t_{1k} + t_{2k} =1,\,\,t_{ik} \geq 0,\,\,\lambda >0$

이 문제의 $t_1,\,...,\,t_n$에 관한 솔루션은 아래와 같은 deterministic detector이다.

$(t_{1k},t_{2k})= \begin{cases} (1,0)\,\,\,\,p_k > \lambda q_k \\ (0,1)\,\,\,\,p_k < \lambda q_k \end{cases}$
만일 $p_k = \lambda q_k$라면 $0 \leq t_{1k} \leq 1,\,t_{2k} = 1-t_{1k}$인 아무 값이 최적값이 된다. 즉 pareto optimal $T$는 randomized detector를 포함한다.

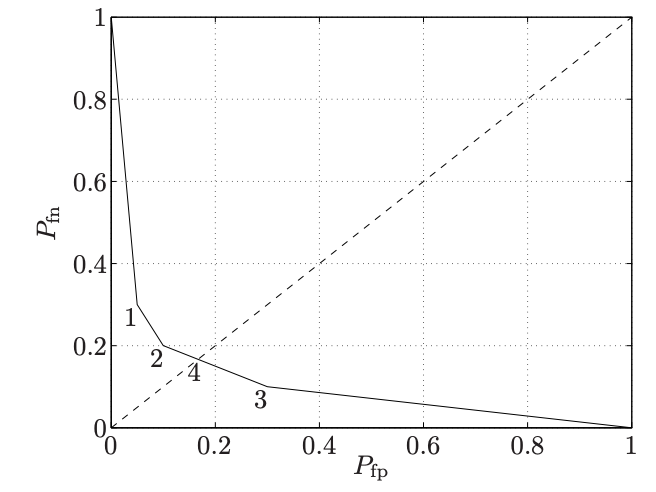
그림은 $P = \begin{bmatrix} 0.7 & 0.1 \\ 0.2 & 0.1 \\ 0.05 & 0.7 \\ 0.05 & 0.1 \end{bmatrix}$일 때 $\lambda$값에 따른 파레토 경계이다. 지점 1,2,3은 deterministic detector, 즉 파레토 경계의 꼭짓점이다. 그리고 지점 4는 randomized detector인 minimax detector$(\min \max\{(Tp)_2,\,(Tq)_1 \})$이다.