4. Chebyshev and Chernoff bounds
Chebyshev bounds
이번에는 우리가 잘 아는 확률에 관한 부등식들을 살펴보고, 이들의 더욱 일반적인 형태가 컨벡스 최적화 문제로 표현될 수 있음을 보일 것이다. 먼저 우리가 잘 아는 R에서 정의된 X에 대한 Markov inequality와 Chebyshev inequality를 살펴보자.
1. Markov inequality.
확률변수 X와 non negative function u(x), 상수 k에 대해 P(u(X)≥k)≤kE(u(X))이다.
2. Chebyshev inequality.
평균이 μ, 분산이 σ2인 확률변수 X와 상수 k에 대해 P(∣X−μ∣≥k)≤kσ2이다.
Markov inequality를 일반화해, S⊆Rm에서 정의된 확률변수 X에 대하여 P(X∈C),C⊆S의 upper bound를 찾고 싶다고 하자. 먼저 C에 대한 indicator function 1C(z)={1z∈C0z∈/C를 정의하자. 우리가 가진 사전 정보는 X에 대한 어떤 함수들 fi에 대한 평균 Efi(X)=ai이다. (이 때 f0(z)=1로 설정하자. 그러면 Ef0(X)=a0=1로 절편 역할을 한다.)
이제 그들의 linear combination f(z)=∑i=0nxifi(z)를 정의하자. 이때 임의의 z∈S에 대하여 f(z)≥1C(z)가 되도록 linear combination을 제한하면, Ef(z)=aTx≥E1C(z)=P(X∈C)임을 알 수 있다. 이때 f(z)와 1C(z)를 최대한 가깝게 선택하면 확률에 대한 가장 타이트한 upper bound를 얻을 수 있다. 즉, 어떤 집합 C에서의 확률에 대한 upper bound는 C의 바깥쪽 경계를 linear function으로 최대한 타이트하게 근사시키는 최적화 문제와 같다. (물론 어디까지나 선형 근사이므로 다른 형태의 더 타이트한 근사가 존재할 수 있다.) 이를 수식으로 정리하면 아래와 같다.
minimizeaTx=x0+a1x1+⋯anxn
subject to∑i=0nxifi(z)≥1∀z∈C
∑i=0nxifi(z)≥0∀z∈S\C
이 문제는 constraint가 linear inequality 형태이므로 컨벡스 최적화 문제이다. 가령 여기에서 S=R+,C=[1,∞),f1(z)=z,Ef1(z)=μ≤1로 설정하면 objective는 x0+x1μ, 제약식은 x0+x1≥1과 x0,x1≥0으로 축약되는 것을 알 수 있다. 0≤μ≤1이므로 이 문제의 최적값은 x0=0,x1=1이다. 따라서 Markov inequality의 가장 단순한 형태인 P(X≥1)≤μ가 도출된다.
이번에는 확률변수 X의 1, 2차 적률(moment)에 대한 정보인 EX=a∈Rm,EXXT=Σ∈Sm를 알고 있다고 해 보자. 이것은 우리가 m개의 z1,...,zm의 평균과 m(m+1)/2개의 z1z1,...,zmzm의 평균에 대한 정보를 가진 것과 같다. 이번에는 이들의 결합인 f(z)=zTPz+2qTz+r,P∈Sm,q∈Rm,r∈R의 quadratic function으로 선택하자. 그러면 Ef(X)=E(XTPX+2qTX+r)=E(tr(PXXT))+2E(qTX)+r=tr(ΣP)+qTa+r이다. 이때 모든 z에 대해 f(z)≥0의 제약식은 linear matrix inequality [PqTqr]⪰0과 동치이다. 이제 Chebyshev bound 문제를 다변수로 확장해 보자. 그러면 우리가 probability bound를 찾고자 하는 집합 C는 다음과 같은 polyhedron의 바깥쪽 집합으로 정의할 수 있다.
C=Rm\P,P={z∣aiTz<bi,i=1,...,k}
이제 z∈C에 대해 f(z)≥1의 제약식은 aiTz≥b⟹zTPz+qTz+r≥1로 표현할 수 있다. 이제 아래의 S-procedure를 이용해 이 제약식 역시 convex constraint로 바꿀 수 있다. 증명은 생략하겠다.
S-procedure
Fi∈Sn,gi∈Rn,hi∈R에 대하여
xTF1x+2g1Tx+h1≥0⟹xTF2x+2g2Tx+h2≥0⟺∃λ≥0s.t.[F2g2Tg2h2]⪰λ[F1g1Tg1h1]
이를 적용하면 이 제약식은 ∃τi,i=1,...,ks.t.[PqTqr−1]⪰τi[0aiT/2ai/2−bi]로 표현될 수 있다. 이제 알아낸 사실들을 정리해 Chebyshev bound를 최적화 문제로 표현하면 아래와 같다.
minimizetr(ΣP)+qTa+r
subject to[PqTqr]⪰0,[PqTqr−1]⪰τi[0aiT/2ai/2−bi]
τi≥0∀i=1,...,k
이 문제는 P,q,r,τ1,...,τk에 대한 SDP에 속한다. 그리고 Optimal value인 α는 평균이 a이고 covariance가 Σ인 임의의 probability distribution에서 P(X∈C)의 upper bound이다.
Chernoff bounds
3. Chernoff bounds.
R에서 정의된 X에 대하여
P(X≥u)≤λ≥0infE(eλ(X−u))⟺logP(X≥u)≤λ≥0inf{−λu+logEeλX}
이 부등식은 사실 Markov inequality에서 u(x)=etx,k=etu로 설정한 것에 불과하다. 그리고 mgf에 로그를 취한 형태인 logEeλX를 cumulant generating function이라고 한다. 이 함수는 항상 convex이기 때문에 이 문제의 목적함수 역시 convex이다. 가령 X가 standard normal distribution일 때 logM(λ)=2λ2이고 −λu+λ2/2의 infimum은 λ=u일 때이므로 P(X≥u)≤e−u2/2의 bound를 얻을 수 있다.
이제 이것을 Rm에서 정의된 X에 대해 확장해 보자. 아까와 같이 우리의 목표는 P(X∈C)에 대한 probability bound를 찾는 것이다. 물론 수치적분이나 몬테카를로 시뮬레이션 등 P(X∈C)를 계산할 방법이 없는 것은 아니지만 이는 보통 아주 많은 계산량을 요구하기 때문에 최적화의 관점에서 더 나은 방법을 찾아보자. Indicator function 1C를 아까와 동일하게 정의하고, λ∈Rm과 μ∈R에 대해 f(z)=eλTz+μ로 정의하자. 이전의 설정과 동일하게 f(z)≥1C(z)가 만족된다면 P(X∈C)=E1C(X)≤Ef(X)의 bound를 찾을 수 있다. 우선 모든 z에 대해 f(z)≥0은 항상 만족되고, z∈C에 대해 f(z)≥1을 만족하려면 λTz+μ≥0이 만족되어야 한다. 따라서 이 조건이 만족될 경우
logP(X∈C)≤μ+logEexp(λTX)를 찾을 수 있다. 여기서부터 아래와 같이 Chernoff bound의 일반적인 형태를 얻는다.
logP(X∈C)≤inf{μ+logEexp(λTX)∣−λTz≤μ}=λinf(z∈Csup(−λTz)+logEexp(λTX))=inf(SC(−λ)+logEexp(λTX))
여기에서 SC는 C의 support function을 뜻한다. 이 문제는 컨벡스 최적화 문제이다. 밑의 예제를 통해 좀 더 살펴보자.
Example. Chernoff bound for a Gaussian variable on a polyhedron
X∼Nm(0,I)라고 가정해 보자. 그러면 cumulant generating function은 logEexp(λTX)=λTλ/2 이다. 그리고 C를 {x∣Ax⪯b}의 polyhedron으로 잡자. 그리고 support function SC를 dual로 표현하면 아래와 같다.
SC(y)=sup{yTx∣Ax⪯b}=−inf{−yTx∣Ax≤b}=−sup{−bTu∣ATu=y,u⪰0}by LP duality=inf{bTu∣ATu=y,u⪰0}
이를 위에서 얻은 식에 대입하면
logP(X∈C)≤λinf(SC(−λ)+logEexp(λTX))=λinfuinf{bTu+λTλ/2∣u⪰0,ATu+λ=0}
이다.
따라서 Chernoff bound는 u,λ에 대한 아래 문제의 optimal value와 같다.
minimizebTy+λTλ/2
subject tou⪰0,ATu+λ=0
이 문제에 대한 기하적인 해석이 가능한데, 우선 위 문제는 아래와 동치이다.
minimizebTu+(1/2)∣∣ATu∣∣22
subject tou⪰0
그리고 이 문제는 아래 문제의 dual이다.
maximize−(1/2)∣∣x∣∣22
subject toATx⪯b
따라서 P(X∈C)≤exp(−dist(0,C)2/2)이다. 이 때 dist(0,C)는 원점에서 C까지의 Euclidean distance를 뜻한다.
5. Experiment design
Optimal experiment design이란 실험계획법의 한 분야로, 우리가 가정한 모델의 파라메터의 편향(bias)과 분산(variance)를 최소화할 수 있는 design matrix를 구성하는 것이다. 어떤 observation a1,…,am으로부터의 linear measurement 모델인 yi=aiTx+wi,i=1,…,m을 고려하자. 이 때 wi가 unit variance를 지닌 iid gaussian noise라면, 우리는 이 모델의 mle가 least-squares solution인 x^=(∑i=1maiaiT)−1∑i=1myiai임을 알고 있다. 그리고 estimation error e=x^−x의 평균은 0이고 covariance matrix는 EeeT=(∑i=1maiaiT)−1이다. 이제부터 이 행렬을 E라고 지칭하자.
이때 paramter x에 대한 α - confidence region은 {x∣(x−x^)TE−1(x−x^)≤F1−α(n,m−n)}으로 나타난다. 행렬 E를 구성하는 a1,…,am이 p개의 가능한 test vector v1,…,vp∈Rn으로부터 선택되었다고 가정하자. 그리고 experiment design의 목적은 E를 가능한 한 작게 만들 수 있는 ai들을 선택하는 것이다. 즉 가능한 p개의 실험으로부터, 최대한의 정보를 뽑아낼 수 있는(most informative) m개의 measurement를 찾아내는 것이 목적이다. mj를 ai가 vj의 값을 가지도록 선택된 개수라고 하자. 그러면 m1+⋯mp=m임을 알 수 있고, E=(∑i=1maiaiT)−1=(∑j=1pmjvjvjT)−1이다. 이때 {v}가 알려져 있기 때문에, error covariance는 각각의 실험이 선택된 수 {mj}에만 의존한다. 따라서 변수 {mj}에 대한 이 최적화 문제는 아래와 같은 vector optimization 문제로 나타낼 수 있다.
minimize (w.r.t.S+n)E=(∑j=1pmjvjvjT)−1
subject tomj≥0,m1+⋯mp=m,mj∈Z
만일 positive semidefinite cone 상에서 E⪯E~라면 우리는 E를 선택했을 때, E~보다 임의의 q에 대하여 qTx의 더 나은(분산이 작은) estimator를 얻을 수 있다. 이제 이 문제의 다양한 변형에 대해 알아보자.
The relaxed experiment design problem
위의 문제는 integer programming 문제이기 때문에 non-convex이고 따라서 큰 규모에서는 풀기 매우 복잡한데, 간단한 조작을 통해 이 문제에 대처할 수 있다. λi=mi/m라고 하자. 즉 λi는 실험 i의 relative frequency를 뜻한다. 그리고 위의 문제를 λ에 대한 문제로 바꾸면 아래와 같다.
minimize (w.r.t.S+n)E=(1/m)(∑j=1pλiviviT)−1
subject toλ⪰0,1Tλ=1
이것을 relaxed experiment design problem이라고 한다. 이 문제는 위와 달리 컨벡스 최적화 문제이다. Constraint 중의 하나인 정수 조건이 빠졌기 때문에 이 문제의 optimal value는 원래 문제의 optimal value의 lower bound이다. 만약 relaxed problem으로부터 정수 조건을 다시 맞추기 위해 mi=round(mλi)로 정의하면 이 솔루션은 sub-optimal solution이 된다. 그리고 sub-optimal한 λi~=(1/m)round(mλi)로 정의하면 ∣λi−λi~∣≤1/2m이므로 m이 커짐에 따라, 즉 데이터가 많아짐에 따라 λ와 λ~는 거의 동일해진다.
그리고 λ는 probability distribution의 관점으로도 해석될 수 있다. 우리의 λ에 대한 선택은 각 실험 ai가 λj의 확률로 vj가 된다는 것을 의미한다. 따라서 λ는 random experiment의 optimal probability distribution이 된다.
Scalarizations
위의 vector optimization 문제를 스칼라에 대한 문제로 바꾸는 몇가지 알려진 기준들에 대해 알아보자. 여기부터는 기본적으로 convexity를 위해 relaxed problem을 전제로 한다.
D-optimal design
이 기준은 confidence ellipsoid의 부피를 가장 작게 만들기 위한 것으로 아래와 같다.
minimizelogdet(∑i=1pλiviviT)−1
subject toλ⪰0,1Tλ=1
E-optimal design
이 기준은 E의 norm(maximum eigenvalue)를 최소화하는 것으로, confidence ellipsoid의 지름(diameter)을 가장 짧게 만들기 위한 것이다. 또한 이 기준은 ∣∣q∣∣2=1인 임의의 q에 대하여 qTe의 분산을 최소화하는 것으로도 해석될 수 있다. 표현은 아래와 같다.
minimize∥∥∥∥(∑i=1pλiviviT)−1∥∥∥∥2
subject toλ⪰0,1Tλ=1
이 문제는 t∈R와 λ∈Rp에 대한 아래의 SDP와 동일한 문제이다.
maximizet
subject to∑i=1pλiviviT⪰tI
λ⪰0,1Tλ=1
A-optimal design
이 기준은 E의 대각합을 최소화하는 것으로, error의 제곱의 평균을 최소화하는 기준이며 이유는 아래와 같다.
E∣∣e∣∣22=Etr(eeT)=trE.
그리고 문제 표현은 아래와 같다.
minimizetr(∑i=1pλiviviT)−1
subject toλ⪰0,1Tλ=1
이 문제 역시 E-optimal design처럼 아래와 같은 SDP로도 표현할 수 있다.
minimize1Tu
subject to[∑i=1pλiviviTekTekuk]⪰0,k=1,…,n
λ⪰0,1Tλ=1
Optimal experiment design and duality
위 세 문제들의 dual problem은 아래와 같다.
Dual of D-optimal, with variable W∈Sn, domain S++n
maximizelogdetW+nlogn
subject toviTWvi≤1,i=1,…,p
Dual of E-optimal, with variable W∈Sn
maximizetrW
subject toviTWvi≤1,i=1,…,p
W⪰0
Dual of A-optimal, with variable W∈Sn
maximize(trW1/2)2
subject toviTWvi≤1,i=1,…,p
예시로 D-optimal design의 dual을 도출하는 과정을 살펴보자.먼저 아래와 같이 primal problem을 X에 대해 재표현한다.
minimizelogdetX−1
subject toX=∑i=1pλiviviT,λ⪰0,1Tλ=1
그리고 dual variable을 도입해 라그랑지안을 도출하면
L(X,λ,Z,z,ν)=logdetX−1+tr(Z(X−∑i=1pλiviviT))−zTλ+ν(1Tλ−1)
이때 X에 대해 미분한 그래디언트를 0으로 놓으면 −X−1+Z=0이고, λi에 대한 minimum은 −viTZvi−zi+ν=0일 때만 존재한다. 따라서 이 조건을 대입하면 dual problem은
maximizen+logdetZ−ν
subject toviTZvi≤ν,i=1,…,p
이고, W=Z/ν로 놓은 뒤 ν에 대해 최적화해 빼내 주면 위의 문제가 도출된다.
위 문제들의 optimal solution W∗는 v1,…,vp를 포함하고 원점을 중점으로 갖는 minimal ellipsoid {x∣xTW∗x≤1}을 결정한다. 또한 W∗와 λ∗는 complementary slackness 조건을 만족하는데, 이는 모든 i에 대해 λi∗(1−viTW∗vi)=0을 만족하므로 optimal experiment design에서는 ellipsoid의 표면에 위치한 실험들만을 선택하게 된다는 뜻이다.
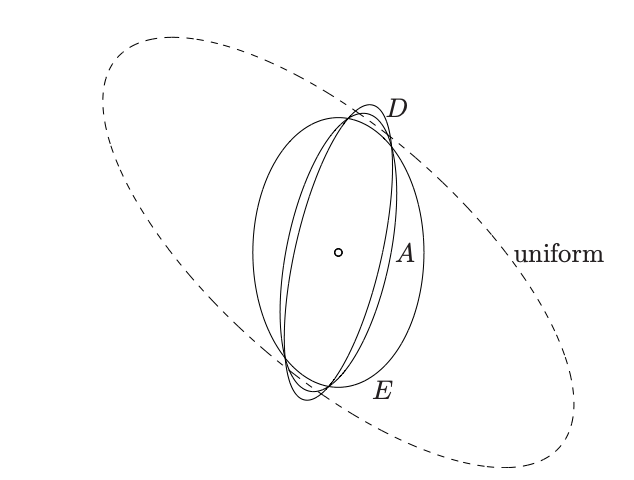
아래는 x∈R2,p=20에서의 예시이다. Optimal design은 원으로 표시된 test vector 중 minimal ellipsoid의 표면에 있는 색칠된 원만을 λ의 비율로 선택하는 것이다.
(1). D-optimal
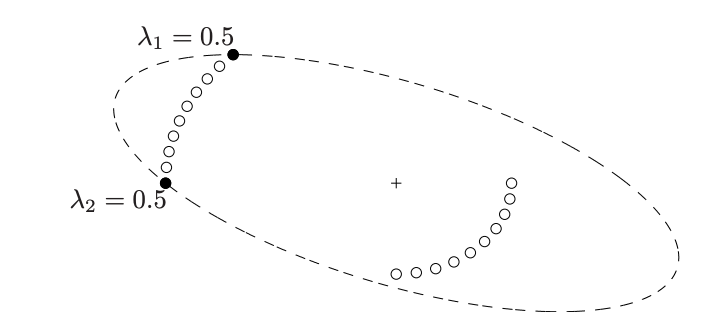
(2). E-optimal
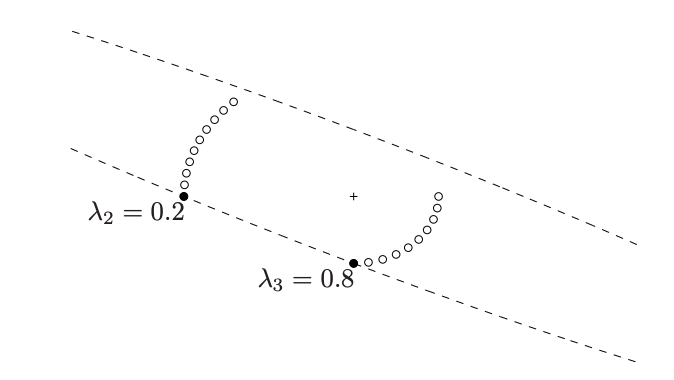
(3). A-optimal
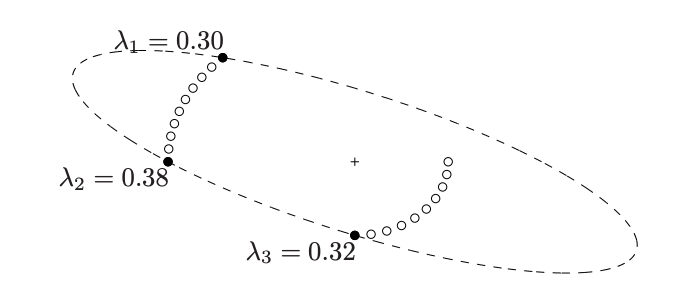
(4). x에 대한 90% confidence ellipsoid의 비교