[Week 3] Convex optimization problems [1]

* 세션 교재: Convex Optimization - Boyd and Vandenberghe. ch.4.

이번 세션부터는 본격적으로 최적화 문제의 형태, 종류, 다양한 예시들에 대해 알아보자.

1. Optimization problems

Basic terminology

최적화 문제의 기본 형태는 아래와 같다.

$\text{minimize}\,\,f_0(x)$
$\begin{aligned} \text{subject to}\,\,&f_i(x) \le0,\quad i=1,\,...,\,m\\ &h_i(x)=0,\quad i=1,\,...,\,p \end{aligned}$

• $f_0: \R^n \rightarrow \R$를 objective function 또는 cost function 이라고 부른다.
• $f_i(x): \R^n \rightarrow \R$들을 inequality constraint function 이라고 부른다.
• $h_i(x): \R^n \rightarrow \R$들을 equality constraint function 이라고 부른다.

Feasible and optimal points

• $x \in \R^n$이 $x \in \textbf{dom}f_0$이고, constraint를 모두 만족하면 $x$를 feasible이라고 한다.
• 이때 $x$가 $f_0,\,f_1,\,...,\,f_m$의 domain에 공통적으로 속하는지의 여부를 implicit constraint라고 하고, equality, inequality 형태로 주어진 조건을 explicit constraint라고 한다.
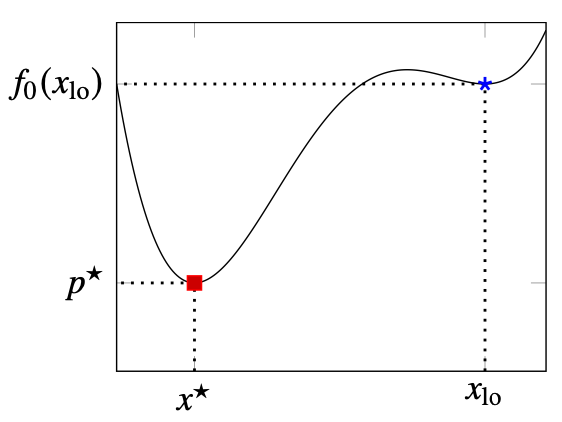
• Optimal value $p^* = \inf\{f_0(x)\,|\,f_i(x) \leq 0,\,\,i=1,\,...,\,m,\,\,h_i(x) = 0,\,\,i=1,\,...,\,p \}$로 정의한다.
• 최적화 문제가 infeasible일 경우, $p^* = \infty$이다.
• 최적화 문제가 unbounded일 경우, $p^* = -\infty$이다.
• Feasible point $x$는 $f_0(x) = p^*$일 경우 Optimal이라고 한다.
• $X_{opt}$는 optimal point의 집합이다.

Locally optimal points

만일 $x$가 $z$에 대한 다음 최적화 문제의 해가 되도록 하는 양수 $R$이 존재한다면 $x$를 locally optimal이라고 한다. 즉 $x$는 주위의 가까운 범위 내에서 목적함수를 최소화한다. 반대로 전체 feasible set에서 목적함수를 최소화하는 $x$를 globally optimal이라 한다.

$\text{minimize}\,\,f_0(z)$
$\begin{aligned} \text{subject to}\,\,&f_i(z) \le0,\quad i=1,\,...,\,m\\ &h_i(z)=0,\quad i=1,\,...,\,p\\ &||z-x||_2 \leq R \end{aligned}$

Feasibility problem

이 문제는 단순히 constraint를 만족하는 $x$를 찾는 문제로 아래처럼 표현할 수 있다.
$\text{find}\,\,x$
$\begin{aligned} \text{subject to}\,\,&f_i(x) \le0,\quad i=1,\,...,\,m\\ &h_i(x)=0,\quad i=1,\,...,\,p \end{aligned}$

이 문제는 objective $f_0(x)=0$인 최적화 문제로 생각할 수 있다.

$\text{minimize}\,\,\,\,0$
$\begin{aligned} \text{subject to}\,\,&f_i(x) \le0,\quad i=1,\,...,\,m\\ &h_i(x)=0,\quad i=1,\,...,\,p \end{aligned}$

Convex optimization problems in standard form

$\text{minimize}\,\,f_0(x)$
$\begin{aligned} \text{subject to}\,\,&f_i(x) \le0,\quad i=1,\,...,\,m\\ &a_i^Tx =b_i,\quad i=1,\,...,\,p \end{aligned}$

위는 컨벡스 최적화 문제의 기본 형태이다. 일반적인 최적화 문제와 달리, 컨벡스 최적화 문제는 domain set, feasible set이 convex이며, objective와 inequality constraint가 convex, equality constraint가 affine이다.

Local and global optima

다음 성질은 왜 우리가 컨벡스 문제를 우선적으로 살펴보는지 말해준다.

컨벡스 최적화 문제의 locally optimal point는 globally optimal이다.

Proof.

• $x$가 locally optimal point이고, 동시에 $f_0(y) < f_0(x)$를 만족하는 feasible $y$가 있다고 가정하자.

• $x$가 locally optimal이라는 것은 $z\,\,\text{feasible},\,\,||z-x||_2\leq R \implies f_0(z) \geq f_0(x)$을 의미한다.

• 이제 $z = \theta y+(1−\theta)x,\,\,\theta = R/(2||y-x||_2)$를 고려하자. 그러면 $||y-x||_2 >R$을 가정했으므로, $0 < \theta < 1/2$이다. 따라서 $z$는 두 feasible point의 convex combination이고, feasible이다.

• 이때 $||z-x||_2 = R/2$이고, convexity에 의해 $f_0(z) \leq \theta f_0(y) + (1-\theta) f_0(x) < f_0(x)$이다. 이는 $x$가 locally optimal이라는 가정에 모순이다. 따라서 $x$는 globally optimal point이다.

이 증명의 마지막 부분은 convexity에 의해 성립하였다.

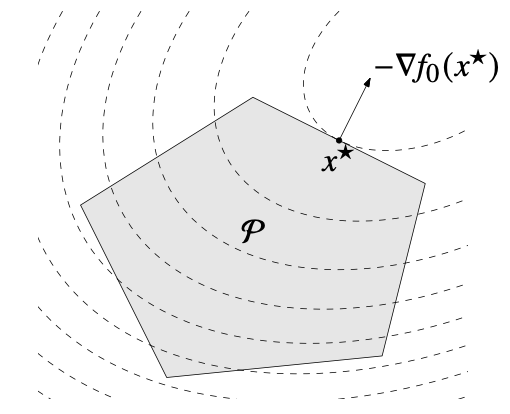
Optimality criterion for differentiable $f_0$

Feasible $x$가 컨벡스 최적화 문제의 해임과 다음이 동치이다.

$\nabla f_0(x)^T (y-x) \geq 0\,\,\forall\,\text{feasible}\,y$

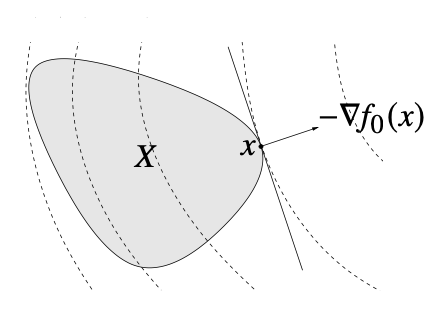
위 그림처럼, gradient $\nabla f_0(x)$는 $0$이 아닐 때 feasible set $X$의 $x$에서의 supporting hyperplane을 이룬다. 그림의 $x$는 feasible set 안에서 함숫값이 가장 작으므로, feasible set 안의 모든 벡터 $y-x$는 $x$에서의 gradient와 예각을 이룬다.

2. Some standard convex problems

이번 섹션에서는 컨벡스 최적화 문제의 카테고리와 가장 대표적인 예시들을 살펴보자. 카테고리는 점점 넓어지는 방식으로 구성되어 있다. 즉 뒤의 것은 앞의 것을 더욱 일반화한 것이다.

Linear program (LP)

선형 최적화 문제이자 가장 기본적인 형태로, 아래와 같이 표현할 수 있다.

$\text{minimize}\,\,c^Tx + d$
$\begin{aligned} \text{subject to}\,\,&Gx \preceq h\\ &Ax=b \end{aligned}$

LP는 산업공학 분야에서 많이 쓰이는데, objective function을 자원 1단위에 대한 비용으로, constraint를 자원량의 제한으로 해석할 수 있는 상황이 많기 때문이다.
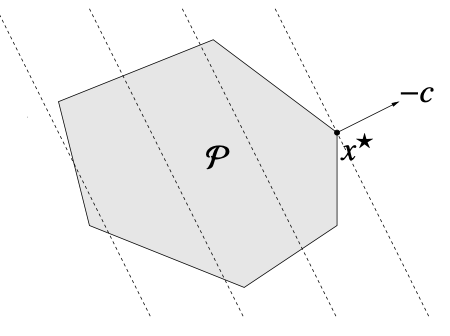
LP의 feasible set은 linear inequality와 eqaulity의 조합으로 나타나므로 아래 그림과 같은 polyhedron 형태를 띈다.

Example: Chebyshev center of a polyhedron

$\text{maximize}\,\,r$
$\begin{aligned} \text{subject to}\,\,&a_i^Tx_c + r \lVert a_i \rVert_2 \leq b_i,\,\,i=1,\,...,\,m \end{aligned}$

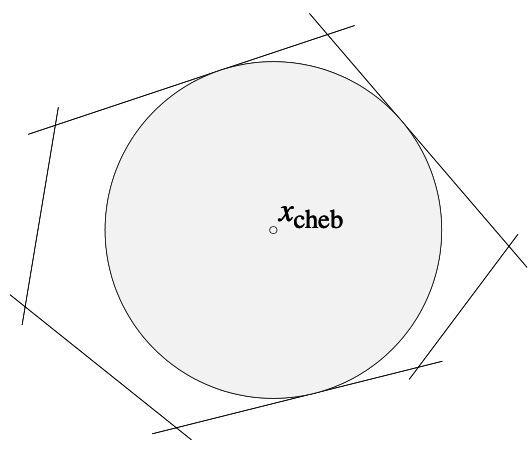
Chebyshev center는 주어진 polyhedron안의 가장 큰 ball의 중심을 말한다. 즉 polyhedron의 가장 깊은 depth를 가진, 가장 경계에서 먼 점이다. Ball을 수식으로 나타내면 $\mathcal{B} = \left\{x_c + u\,\,|\,\lVert u \rVert_2 \leq r \right\}$이고, 이를 constraint(polyhedron 안)에 대입하면 $a_i^T(x_c + u) \leq b_i$인데, 여기서 부등식 좌변의 경계, 즉 좌변에서 가장 큰 값은 ball의 표면 상의 점이 된다. 따라서 부등식을 $a_i^Tx_c + r \lVert a_i \rVert_2 \leq b_i$로 다시 쓸 수 있고, 이 constraint 안에서 $r$을 maximize하는 문제로 표현할 수 있다.

Quadratic program (QP)

목적함수를 convex quadratic function으로 일반화한 것으로, 일반화된 표현은 아래와 같다.

$\text{minimize}\,\,(1/2)x^TPx + q^Tx+r$
$\begin{aligned} \text{subject to}\,\,&Gx \preceq h\\ &Ax=b \end{aligned}\\$
$\text{with}\,\,P \in \mathbb{S}^n_+$

Feasible set은 이전과 동일한 polyhedron이나, 목적함수가 달라졌으므로 점선으로 표시된 sublevel set의 형태가 다르다.

Example: Linear program with random cost

LP의 목적함수에서 벡터 $c$가 정해진 값이 아니라 평균이 $\bar{c}$이고 covariance가 $\Sigma$인 random variable이라고 하자. 이때 risk-averse problem이란 주어진 random variable cost의 평균과 분산의 trade-off 관계를 고려하여 최적의 조합을 찾는 문제이다. 가령 포트폴리오 최적화 문제에서 평균 수익을 극대화함과 동시에, 높은 수익을 기대할수록 분산(리스크)가 커지는 것을 고려해 최적화 문제를 푼다. 이 문제는 아래와 같이 표현할 수 있다. 이때 $\gamma$는 리스크를 얼마나 고려할지에 대한 hyperparameter이다.

$\text{minimize}\,\,E(-c^Tx)+\gamma Var(c^Tx)$
$\begin{aligned} \text{subject to}\,\,&Gx \preceq h\\ &Ax=b \end{aligned}$

이는 다시 아래와 같은 QP와 동치이다.

$\text{minimize}\,\,-\bar{c}^Tx+x^T\Sigma x$
$\begin{aligned} \text{subject to}\,\,&Gx \preceq h\\ &Ax=b \end{aligned}$

Quadratically constrained quadratic program (QCQP)

목적함수에 더해 constraint 역시 linear inequality에서 quadratic inequality로 일반화한 것으로, 일반적인 형태는 아래와 같다.

$\text{minimize}\,\,(1/2)x^TP_0x + q_0^Tx+r_0$
$\begin{aligned} \text{subject to}\,\,&(1/2)x^TP_ix + q_i^Tx+r_i \leq0,\,\,i=1,\,...,\,m\\ &Ax=b \end{aligned}\\$
$\text{with}\,\,P_i \in \mathbb{S}^n_+$

만일 constraint에서 $P_i \in \mathbb{S}^n_{++}$라면 feasible set은 ellipsoid와 affine set의 교집합이 된다.

Second-order cone programming

LP의 constraint가 second-order cone inequality로 일반화된 것으로, 일반적인 형태는 아래와 같다.

$\text{minimize}\,\,f^Tx$
$\begin{aligned} \text{subject to}\,\,&||A_ix+b_i||_2\leq c_i^Tx +d_i,\,\,i=1,\,...,\,m\\ &Fx=g \end{aligned}\\$
$\text{with}\,\,A_i \in \R^{n_i \times n},\,F\in \R^{p \times n}$

Constraint의 $(A_ix+b_i, c_i^Tx +d_i)$가 $\R^{n_i+1}$상의 second-order cone이므로 붙은 이름으로, 만일 $n_i=0$이면 이 문제는 LP가 되고, $c_i=0$이면 QCQP가 된다.

Example: Robust linear programming

(매우)나중 세션에서 자세히 다룰 내용이므로 간단히만 살펴보자.
다음과 같은 LP의 constraint vector $a_i$에 uncertainty가 있다고 가정해 보자. 즉 $a_i$의 값이 표시된 것에서 일정 범위만큼 변할 수 있고, 이를 고려해서 최적화를 하는 상황이다.

$\text{minimize}\,\,c^Tx$
$\begin{aligned} \text{subject to}\,\,a_i^Tx \leq b_i,\,i=1,\,...,\,m \end{aligned}$

이때 $a_i$에 대한 불확실성을 다룰 수 있는 접근에는 크게 두 가지가 있다.
첫 번째로 $a_i$가 변할 수 있는 범위를 적절히 추정해, 그 범위 내에서도 constraint가 무조건 만족되도록 문제를 푸는 것이다. 가령 $a_i$의 범위를 ellipsoid $\mathcal{E}_i =\{\bar{a}_i+P_i u\,|||u||_2 \leq 1\}$로 잡자. 그러면 $\sup_{||u||_2 \leq 1}(\bar{a}_i +P_i u)^T = \bar{a}_i^Tx+||P_i^Tx||_2$이므로 이 문제는 다음과 같은 SOCP로 표현된다.

$\text{minimize}\,\,c^Tx$
$\begin{aligned} \text{subject to}\,\,\bar{a}_i^Tx+||P_i^Tx||_2 \leq b_i,\,i=1,\,...,\,m \end{aligned}$

두 번째로 가능한 접근은 불확실성이 어떤 확률분포를 따른다고 가정하고, constraint가 정해진(높은) 확률로 만족되도록 문제를 푸는 것이다. 이번에는 $a_i \sim N(\bar{a}_i, \Sigma_i)$라고 해 보자. 그러면 $\mathbb{P}(a_i^Tx \leq b_i) = \Phi\left(\frac{b_i-\bar{a}_i^T x}{||\Sigma_i^{1/2} x||_2}\right)$이므로 constraint가 최소 $\eta$의 확률로 만족되도록 $(\mathbb{P}(a_i^Tx \leq b_i) \geq \eta)$설정하면, $\eta \geq 1/2$에 대해 이 문제는 아래의 SOCP와 같다.

$\text{minimize}\,\,c^Tx$
$\begin{aligned} \text{subject to}\,\,\bar{a}_i^Tx+\Phi^{-1}(\eta)||\Sigma_i^{1/2} x||_2 \leq b_i,\,i=1,\,...,\,m \end{aligned}$