[Week 3] Convex optimization problems [2]

2. Some standard convex problems, cont'd

Conic form problem

이 문제는 LP를 generalized inequality로 확장한 것으로, 일반적인 형태는 아래와 같다.

$\text{minimize}\,\,c^Tx$
$\begin{aligned} \text{subject to}\,\,&Fx+g \preceq_K 0\\ &Ax=b \end{aligned}$

만일 proper cone $K = \mathbb{R}_+^m$으로 정의하면 이 문제는 LP와 동일하다.

Semidefinite program (SDP)

이 문제는 교재에서 다루는 convex problem의 가장 일반적인 형태이다. 수식으로 표현하면 다음과 같다.

$\text{minimize}\,\,c^Tx$
$\begin{aligned} \text{subject to}\,\,&x_1F_1 + x_2F_2 + \cdots +x_nF_n +G \preceq 0\\ &Ax=b \end{aligned}\\$
$\text{with}\,\,F_i,G \in \mathbb{S}^k$

이런 형태의 inequality constraint를 Linear matrix inequality(LMI) 로 부른다. 만일 문제에 여러 개의 LMI를 넣고 싶다고 하면, 이는 $x_1 \begin{bmatrix}\hat{F}_1 & 0 \\ 0 & \tilde{F}_1 \end{bmatrix}+ x_2\begin{bmatrix}\hat{F}_2 & 0 \\ 0 & \tilde{F}_2 \end{bmatrix}+\cdots+\begin{bmatrix}\hat{G} & 0 \\ 0 & \tilde{G} \end{bmatrix} \preceq 0$의 constraint와 동일하다.

Example: Matrix norm minimization

$A(x) = A_0 + x_1A_1 + \cdots + x_nA_n\,\,(A_i \in \R^{p \times q})$가 주어졌을 때, 이 행렬의 norm $||A(x)||_2 = (\lambda_{\max}(A(x)^TA(x)))^{1/2}$을 최소화하고 싶다고 하자. 이런 문제는 이미지 데이터 처리, 차원 축소 등에 응용될 수 있다. 이 문제는 $x \in \R^n,\,t \in \R$에 대한 SDP로 다음과 같이 나타낼 수 있다.

$\text{minimize}\,\,t$
$\begin{aligned} \text{subject to}\,\,&\begin{bmatrix}tI & A(x) \\ A(x)^T & tI \end{bmatrix}\succeq 0\\ \end{aligned}\\$

이때 constraint는 $||A||_2 \leq t \iff A^TA \preceq t^2I$이므로 위와 같이 도출된 것이다.

3. Transforming problems

어떤 상황이 주어지고 이를 최적화 문제로 나타냈을 때, 나타낸 문제를 풀기 쉬운 형태로 적절히 변형하는 것은 매우 중요하다. 이번 섹션에서는 대표적인 변형 테크닉들을 알아보자.

Change of variables

Optimization variable $x \in \R^n$에 어떤 일대일함수 $\phi: \R^n \rightarrow \R^n$을 씌워도 $\phi(x)$가 problem domain을 벗어나지 않는다면 $\tilde{f}_i(z) = f_i(\phi(z))$와 같이 $x = \phi(z)$로 놓고 $z$에 대해 문제를 풀어도 된다. 예시를 통해 살펴보자.

다음 non-convex problem을 보자.
$\text{minimize}\,\,x_1/x_2 + x_3/x_1$
$\begin{aligned} \text{subject to}\,\,&x_2/x_3+x_1 \leq1\\ \end{aligned}\\ \text{with}\,\,x \succ 0$

이 문제에서 $x = \exp(z)$로 놓으면 문제는 아래와 같이 바뀐다.
$\text{minimize}\,\,\exp(z_1-z_2) + \exp(z_3-z_1)$
$\begin{aligned} \text{subject to}\,\,&\exp(z_2-z_3)+\exp(z_1) \leq1\\ \end{aligned}$

이처럼 간단한 변환을 통해 문제를 convex problem으로 바꿀 수도 있다.

Transformation of objective and constraint functions

만일 $\phi_0$가 monotone increasing이고,
$\psi_i(u) \leq 0 \iff u \leq 0,$
$\varphi_i(u)=0\iff u = 0$
의 조건이 성립하면 원래의 최적화 문제의 함수들에 이들을 씌워 아래처럼 변환해도 동일한 해를 얻는다. 가령 $||Ax-b||$의 minimization이 $||Ax-b||^2$의 minimization과 동일한 것과 같은 원리이다.

$\text{minimize}\,\,\,\phi_0(f_0(x))$
$\begin{aligned} \text{subject to}\,\,&\psi_i(f_i(x)) \le0,\quad i=1,\,...,\,m\\ &\varphi_i(h_i(x))=0,\quad i=1,\,...,\,p \end{aligned}$

Converting maximization to minimization

$\phi_0$가 monotone decreasing이면 목적 함수에 이것을 씌워 $\phi_0(f_0(x))$로 쓰고, maximization 문제를 minimization 문제로 뒤집어도 동일하다. 목적함수의 부호를 뒤집는 것과 같은 원리이다.

Eliminating equality constraints

$\text{minimize}\,\,\,f_0(x)$
$\begin{aligned} \text{subject to}\,\,&f_i(x) \le0,\quad i=1,\,...,\,m\\ &Ax=b \end{aligned}$
는 아래와 동일하다.

$\text{minimize(over }z)\,\,\,f_0(Fz+x_0)$
$\begin{aligned} \text{subject to}\,\,&f_i(Fz+x_0) \le0,\quad i=1,\,...,\,m \end{aligned}$
where $F$ and $x_0$ are such that $Ax=b$
$\iff x=Fz+x_0$ for some $z$

Introducing equality constraints

위의 정반대 방법이다.
$\text{minimize}\,\,\,f_0(A_0x+b_0)$
$\begin{aligned} \text{subject to}\,\,&f_i(A_ix+b_i) \le0,\quad i=1,\,...,\,m\end{aligned}$
은 아래와 동일하다.

$\text{minimize(over }x,y_i)\,\,\,f_0(y_0)$
$\begin{aligned} \text{subject to}\,\,&f_i(y_i) \le0,\quad i=1,\,...,\,m \\ &y_i=A_ix+b_i,\quad i=0,\,...,\,m\end{aligned}$

Introducing slack variables for linear inequalities

Soft-margin SVM에 응용된 테크닉이다.
$\text{minimize}\,\,\,f_0(x)$
$\begin{aligned} \text{subject to}\,\,&a_i^Tx \le b_i,\quad i=1,\,...,\,m\end{aligned}$
은 아래와 동일하다.

$\text{minimize}\,\,\,f_0(x)$
$\begin{aligned} \text{subject to}\,\,&a_i^Tx +s_i = b_i,\quad i=1,\,...,\,m \\ &s_i \geq 0,\quad i=1,\,...,\,m\end{aligned}$

Epigraph form

목적함수를 epigraph로 보고 변수 $t$를 도입해 아래와 같이 표현할 수 있다.

$\text{minimize}\,\,t$
$\begin{aligned} \text{subject to}\,\,&f_0(x)-t \leq 0\\ &f_i(x) \leq 0\quad i=1,\,...,\,m \\ &Ax=b\end{aligned}$

Minimizing over some variables

두 변수에 대한 최적화 문제
$\text{minimize}\,\,f_0(x_1,x_2)$
$\begin{aligned} \text{subject to}\,\,&f_i(x_1) \leq 0\quad i=1,\,...,\,m \\ \end{aligned}$
는 $\tilde{f}_0(x_1) = \inf_{x_2}f_0(x_1,x_2)$로 놓으면 아래와 동일하다.

$\text{minimize}\,\,\tilde{f}_0(x_1)$
$\begin{aligned} \text{subject to}\,\,&f_i(x_1) \leq 0\quad i=1,\,...,\,m \\ \end{aligned}$

Convex relaxation

Example: Boolean LP

다음과 같이 $0$ 또는 $1$의 값만 가지는 boolean variable이 포함된 LP 문제가 있다.

$\text{minimize}\,\,c^T(x,z)$
$\begin{aligned} \text{subject to}\,\,&F(x,z) \preceq g,\,\,A(x,z)=b,\,\,z\in\{0,1\}^q \\ \end{aligned}$

이런 문제는 일반적으로 non-convex여서 풀기 쉽지 않다. 이때 constraint set의 convex hull을 고려하자. 즉, $z\in [0,1]^q$로 relaxation한다. 이렇게 푼 문제의 optimal value는 원래 문제의 optimal value의 lower bound이다. 마찬가지로 objective가 non-convex인 경우에도 그것의 convex lower bound를 찾아서, 약간의 오차를 감수하는 대신 문제를 훨씬 간단하게 풀 수 있다.

4. Quasiconvex optimization

Quasiconvex optimization은 objective function이 quasiconvex function이며, constraint function이 convex한 형태이다.
Quasiconvex 문제의 경우 convex와 다르게 locally optimal point가 globally optimal point가 아닐 수 있음에 주의해야 한다.

LP의 일반화인 Linear-fractional programming, Von Neumann growth model 등이 대표적인 quasiconvex 문제이다.

Convex representation of sublevel sets

$f_0$가 quasiconvex라면, 다음과 같은 $\phi_t$가 존재한다.

• $t$를 고정했을 때, $x$에 대해 convex
• $f_0$의 $t$-sublevel set은 $\phi_t$의 $0$-sublevel set (i.e. $f_0(x)\leq t \iff \phi_t(x)\leq0$)

따라서 $t$를 고정하고 다음과 같은 convex feasibility 문제를 풀었을 때,

$\text{find}\,\,x$
$\begin{aligned} \text{subject to}\,\,&\phi_t(x) \leq 0\\ &f_i(x)\leq 0,\,\,i=1,\,...,\,m\\ &Ax=b\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(1)\end{aligned}$

Feasible이면 $t \geq p^*$이고, infeasible이면 $t \leq p^*$이다.

Bisection method for quasiconvex optimization

이를 이용한 bisection 알고리즘은 다음과 같다.

$\textbf{given}\,\,l \leq p^*,\,u \geq p^*,\,\text{tolerance}\,\,\epsilon >0.$
$\textbf{repeat}\\ \quad1.\,t:=(l+u)/2.\\ \quad2.\,\text{Solve the convex feasibility problem (1)}.\\ \quad3.\,\textbf{if}\text{(1) is feasible, }u:=t;\quad\textbf{else }l:=t.\\ \textbf{until }u-l \leq \epsilon.$

이 알고리즘은 수렴하는 데 $\lceil \log_2((u-l)/\epsilon \rceil$번의 반복이 요구된다.

5. Multicriterion optimization

최적화 문제의 목적함수 값이 스칼라가 아니라 벡터인 경우, 이런 종류의 문제를 vector optimization이라고 한다.
$f_0(x) = (F_1(x),\,F_2(x),\,...,F_q(x))$로 구성된 objective를 전부 명백하게 minimize하는 $x^*$는 존재하지 않을 때가 많다. 일반적으로는 목적함수 중 일부분의 이점을 얻기 위하여 다른 부분의 이점을 일부 포기해야 하는 trade-off 관계가 있으며, 최적화 시 이를 반드시 고려해야 한다.

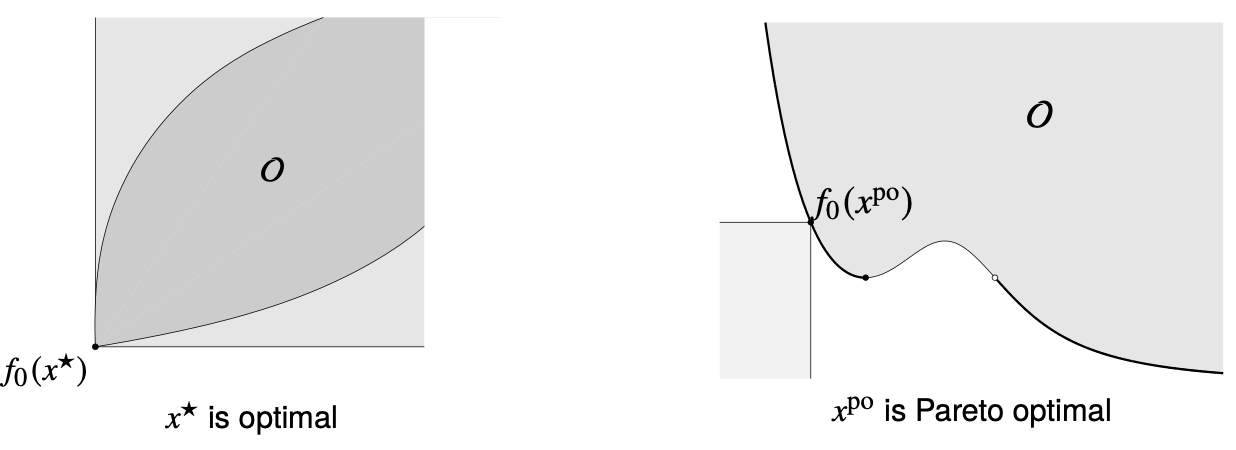
Pareto optimality

Feasible한 $x$와 다른 feasible한 $\tilde{x}$에 대하여 $f_0(x) \preceq f_0(\tilde{x})$이고, 최소 한 개의 $i$에 대하여 $F_i(x) < F_i(\tilde{x})$일 때 $x$가 $\tilde{x}$를 dominate한다고 부른다. 만일 feasible한 $x^{po}$가 다른 feasible point에 dominate되지 않을 경우, $x^{po}$를 Pareto optimal이라고 부른다. 다시 말해 $x^{po}$보다 명백히 우월한 상태가 가능하지 않고, $x^{po}$에서 특정 부분을 개선하기 위해서는 반드시 다른 부분을 포기해야 한다는 뜻이다. Pareto optimal point는 여러 개가 존재할 수 있으며, $q=2$일 경우 파레토 최적인 지점의 목적함수 값들은 optimal trade-off curve를 이루고, $q=3$일 경우 optimal trade-off surface를 이룬다. 집합의 관점에서 optimal point는 minimum element를 뜻하고, pareto optimal point는 minimal element를 뜻한다.

Scalarization

vector optimization 문제를 푸는 가장 간단한 테크닉은 scalarization으로, 말 그대로 목적함수를 스칼라로 바꿔 주는 것이다. $\lambda \succ 0$을 선택해, 목적함수를 아래와 같이 바꿔 준다.

$\lambda^Tf_0(x) = \lambda_1F_1(x)+\lambda_2F_2(x)+\cdots +\lambda_qF_q(x)$

이 목적함수의 optimal point $x$는 pareto optimal이다.
이때 $\lambda$는 목적함수의 구성 요소 중 무엇을 우선시할 것인지를 나타내는 상대적 가중치이다. 가령 최소화 문제에서 $i$번째 가중치를 크게 잡으면, 그 요소가 조금만 커져도 목적함수 값이 크게 증가하므로 그 요소의 값을 우선적으로 고려하게 된다.
이전 1주차 세션에서 배웠듯, convex problem이 아닌 이상 scalarization을 통해 모든 pareto optimal point를 찾아낼 수는 없다. 아래 그림에서 $x_3$은 pareto optimal이지만 scalarization을 통해 찾아지지 않는다.

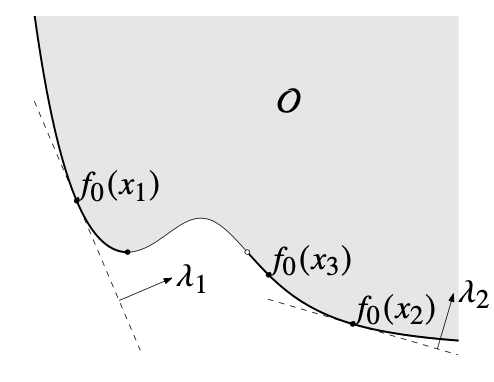
Convex problem의 경우 이론상 $\lambda \succeq_{K^*} 0$을 바꿔 가며 모든 pareto optimal point를 찾을 수 있다. (등호가 들어간 이유는 몇몇 극단적인 경우, 가령 수직 접선에서의 optimal point 때문이다.) 그러나 $\lambda \succ_{K^*} 0$에서 찾은 모든 지점은 pareto optimal이지만, $\lambda \succeq_{K^*} 0$에서 찾은 지점은 pareto optimal이 아닐 수 있으므로 따로 체크해 주어야 한다. 이는 1주차 세션 마지막 내용과 일치한다.

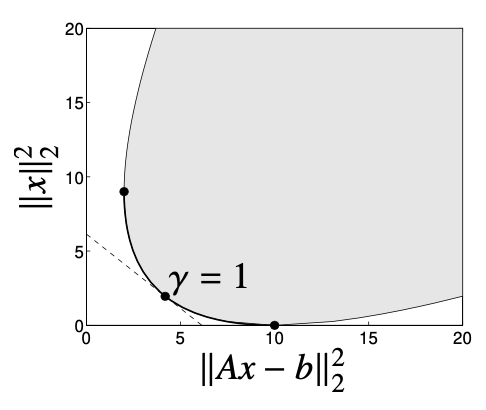
Example: Regularized least-squares

$\text{minimize(w.r.t }\R^2_+)\,\,(||Ax-b||_2^2,||x||_2^2)$

$\gamma >0$에 대해 $\lambda = (1,\gamma)$로 선택하자. 아래 그림은 trade-off curve이며, limiting case($\gamma \rightarrow 0,\,\gamma \rightarrow \infty$, 양쪽의 두 경계)만 제외하고 sclarization을 통해 굵은 실선의 모든 pareto optimal
$x = ((A^TA)+\gamma I)^{-1}A^Tb$을 찾아낼 수 있다.