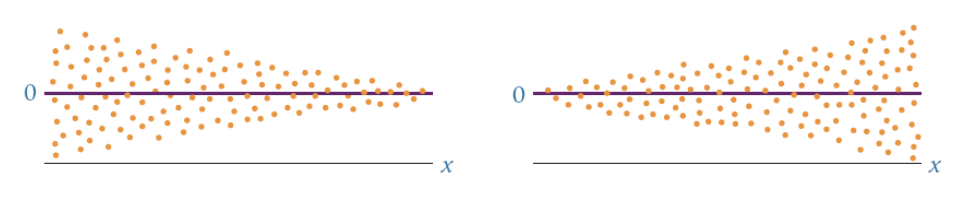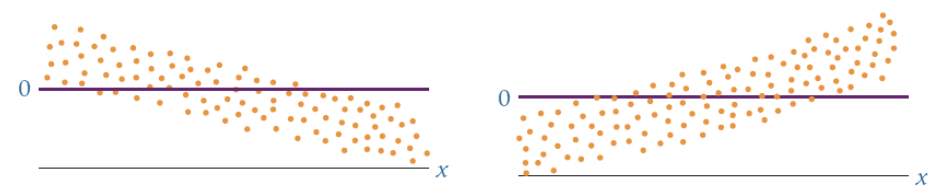Simple Regression Analysis and Correlation
Correlation Coefficient
Pearson's Correlation Coefficient
Sample coefficient of correlation
r = ∑ ( x − x ˉ ) ( y − y ˉ ) ∑ ( x − x ˉ ) 2 ∑ ( y − y ˉ ) 2 = ∑ x y − ∑ x ∑ y n ( ∑ x 2 − ( ∑ x ) 2 n ) ( ∑ y 2 − ( ∑ y ) 2 n ) r=\frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^2 \sum(y-\bar{y})^2}}=\frac{\sum x y-\frac{\sum x \sum y}{n}}{\sqrt{\left(\sum x^2-\frac{\left(\sum x\right)^2}{n}\right)\left(\sum y^2-\frac{\left(\sum y\right)^2}{n}\right)}} r = ∑ ( x − x ˉ ) 2 ∑ ( y − y ˉ ) 2 ∑ ( x − x ˉ ) ( y − y ˉ ) = ( ∑ x 2 − n ( ∑ x ) 2 ) ( ∑ y 2 − n ( ∑ y ) 2 ) ∑ x y − n ∑ x ∑ y
-1<r<1
r is symmetric
Correlation does not imply Causation
linear regression
y i = β 0 + β 1 x i + ϵ i , i = 1 , … , n where ϵ i ∼ i.i.d N ( 0 , σ 2 ) y_i=\beta_0+\beta_1 x_i+\epsilon_i, \quad i=1, \ldots, n \quad \text { where } \epsilon_i \stackrel{\text { i.i.d }}{\sim} \mathcal{N}\left(0, \sigma^2\right) y i = β 0 + β 1 x i + ϵ i , i = 1 , … , n where ϵ i ∼ i.i.d N ( 0 , σ 2 )
y i = β 0 + β 1 x i + ϵ i , i = 1 , … , n y_i=\beta_0+\beta_1 x_i+\epsilon_i, \quad i=1, \ldots, n y i = β 0 + β 1 x i + ϵ i , i = 1 , … , n assumptions: ϵ i ∼ N ( 0 , σ 2 ) \epsilon_i \sim \mathcal{N}\left(0, \sigma^2\right) ϵ i ∼ N ( 0 , σ 2 )
Therefore, y i ∼ N ( β 0 + β 1 x i , σ 2 ) y_i \sim \mathcal{N}\left(\beta_0+\beta_1 x_i, \sigma^2\right) y i ∼ N ( β 0 + β 1 x i , σ 2 )
prediction
we use a deterministic model to predict the value of y
y ^ = b 0 + b 1 x \hat{y}=b_0+b_1 x y ^ = b 0 + b 1 x
최소제곱법; Least Squares
예측값과 실제 값의 차이를 최소화 시킨다.
min b 0 , b 1 ∑ i = 1 n ( y i − b 0 − b 1 x i ) 2 = min b 0 , b 1 ∑ i = 1 n ( y i − y ^ i ) 2 \min _{b_0, b_1} \sum_{i=1}^n\left(y_i-b_0-b_1 x_i\right)^2=\min _{b_0, b_1} \sum_{i=1}^n\left(y_i-\hat{y}_i\right)^2 b 0 , b 1 min i = 1 ∑ n ( y i − b 0 − b 1 x i ) 2 = b 0 , b 1 min i = 1 ∑ n ( y i − y ^ i ) 2 proof
S S = ∑ i = 1 n ( y i − b 0 − b 1 x i ) 2 \mathrm{SS}=\sum_{i=1}^n\left(y_i-b_0-b_1 x_i\right)^2 S S = i = 1 ∑ n ( y i − b 0 − b 1 x i ) 2 Step 1. b0으로 미분 후 =0
∂ S S ∂ b 0 = − 2 ∑ i = 1 n ( y i − b 0 − b 1 x i ) = 0 \frac{\partial \mathrm{SS}}{\partial b_0}=-2 \sum_{i=1}^n\left(y_i-b_0-b_1 x_i\right)=0 ∂ b 0 ∂ S S = − 2 i = 1 ∑ n ( y i − b 0 − b 1 x i ) = 0 b 0 = 1 n ∑ i = 1 n ( y i − b 1 x i ) = y ˉ − b 1 x ˉ b_0=\frac{1}{n} \sum_{i=1}^n\left(y_i-b_1 x_i\right)=\bar{y}-b_1 \bar{x} b 0 = n 1 i = 1 ∑ n ( y i − b 1 x i ) = y ˉ − b 1 x ˉ Step 2. b1로 미분 후 =0
∂ S S ∂ b 1 = − 2 ∑ i = 1 n x i ( y i − b 0 − b 1 x i ) = 0 \frac{\partial \mathrm{SS}}{\partial b_1}=-2 \sum_{i=1}^n x_i\left(y_i-b_0-b_1 x_i\right)=0 ∂ b 1 ∂ S S = − 2 i = 1 ∑ n x i ( y i − b 0 − b 1 x i ) = 0 Step 3. 위의 b0을 대입
∑ i = 1 n x i ( ( y i − y ˉ ) − b 1 ( x i − x ˉ ) ) = 0 \sum_{i=1}^n x_i\left(\left(y_i-\bar{y}\right)-b_1\left(x_i-\bar{x}\right)\right)=0 i = 1 ∑ n x i ( ( y i − y ˉ ) − b 1 ( x i − x ˉ ) ) = 0 b 1 = ∑ i = 1 n x i ( y i − y ˉ ) ∑ i = 1 n ( x i ( x i − x ˉ ) ) b_1=\frac{\sum_{i=1}^n x_i\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i\left(x_i-\bar{x}\right)\right)} b 1 = ∑ i = 1 n ( x i ( x i − x ˉ ) ) ∑ i = 1 n x i ( y i − y ˉ ) ∑ i = 1 n x i ( y i − y ˉ ) ∑ i = 1 ( x i ( x i − x ˉ ) ) = ∑ i = 1 n ( x i − x ˉ + x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ + x ˉ ) ( x i − x ˉ ) = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) + ∑ i = 1 n x ˉ ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) ( x i − x ˉ ) + ∑ i = 1 n x ˉ ( x i − x ˉ ) = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 \frac{\sum_{i=1}^n x_i\left(y_i-\bar{y}\right)}{\sum_{i=1}\left(x_i\left(x_i-\bar{x}\right)\right)}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}+\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}+\bar{x}\right)\left(x_i-\bar{x}\right)}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)+\sum_{i=1}^n \bar{x}\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(x_i-\bar{x}\right)+\sum_{i=1}^n \bar{x}\left(x_i-\bar{x}\right)}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} ∑ i = 1 ( x i ( x i − x ˉ ) ) ∑ i = 1 n x i ( y i − y ˉ ) = ∑ i = 1 n ( x i − x ˉ + x ˉ ) ( x i − x ˉ ) ∑ i = 1 n ( x i − x ˉ + x ˉ ) ( y i − y ˉ ) = ∑ i = 1 n ( x i − x ˉ ) ( x i − x ˉ ) + ∑ i = 1 n x ˉ ( x i − x ˉ ) ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) + ∑ i = 1 n x ˉ ( y i − y ˉ ) = ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∗ ∑ i = 1 n ( x i − x ˉ ) = 0 ∗ ∑ i = 1 n ( y i − y ˉ ) = 0 \begin{aligned} & * \sum_{i=1}^n\left(x_i-\bar{x}\right)=0 \\ & * \sum_{i=1}^n\left(y_i-\bar{y}\right)=0 \end{aligned} ∗ i = 1 ∑ n ( x i − x ˉ ) = 0 ∗ i = 1 ∑ n ( y i − y ˉ ) = 0 최종
b 0 = y ˉ − b 1 x ˉ b 1 = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 . \begin{aligned} & b_0=\bar{y}-b_1 \bar{x} \\ & b_1=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} . \end{aligned} b 0 = y ˉ − b 1 x ˉ b 1 = ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) . residual
the least squares regression minimizes the sum of squared residuals
∑ i = 1 n ( y i − y ^ i ) 2 = ∑ i = 1 n e i 2 \sum_{i=1}^n\left(y_i-\hat{y}_i\right)^2=\sum_{i=1}^n e_i^2 i = 1 ∑ n ( y i − y ^ i ) 2 = i = 1 ∑ n e i 2 linear regression assumes
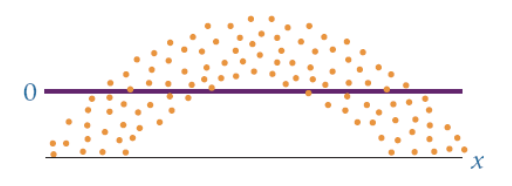
The model is linear
The error terms have constant variances The error terms are independent
The error terms are normally distributed
model is not linear
errors do not have a constant variance
errors are not independent
sum of squares of the residual (=SS)
S S E = ∑ i = 1 n ( y i − y ^ i ) 2 \mathrm{SSE}=\sum_{i=1}^n\left(y_i-\hat{y}_i\right)^2 S S E = i = 1 ∑ n ( y i − y ^ i ) 2 mean square error
MSE = S S E n − 2 \text { MSE }=\frac{S S E}{n-2} MSE = n − 2 S S E E [ M S E ] = σ 2 \mathbb{E}[\mathrm{MSE}]=\sigma^2 E [ M S E ] = σ 2 standard error of the estimate
s e = M S E = S S E n − 2 s_e=\sqrt{\mathrm{MSE}}=\sqrt{\frac{\mathrm{SSE}}{n-2}} s e = M S E = n − 2 S S E r 2 r^2 r 2
0 < r 2 < 1 0<r^2<1 0 < r 2 < 1 r 2 r^2 r 2
observed data:
y i = y ^ i + ( y i − y ^ i ) y_i=\hat{y}_i+\left(y_i-\hat{y}_i\right) y i = y ^ i + ( y i − y ^ i ) subtract y ˉ \bar y y ˉ
y i − y ˉ = ( y ^ i − y ˉ ) + ( y i − y ^ i ) y_i-\bar{y}=\left(\hat{y}_i-\bar{y}\right)+\left(y_i-\hat{y}_i\right) y i − y ˉ = ( y ^ i − y ˉ ) + ( y i − y ^ i ) important three quantities
S S T = ∑ ( y i − y ˉ ) 2 S S R = ∑ ( y ^ i − y ˉ ) 2 S S E = ∑ ( y i − y ^ i ) 2 \begin{aligned} & \mathrm{SST}=\sum\left(y_i-\bar{y}\right)^2 \\ & \mathrm{SSR}=\sum\left(\hat{y}_i-\bar{y}\right)^2 \\ & \mathrm{SSE}=\sum\left(y_i-\hat{y}_i\right)^2 \end{aligned} S S T = ∑ ( y i − y ˉ ) 2 S S R = ∑ ( y ^ i − y ˉ ) 2 S S E = ∑ ( y i − y ^ i ) 2 SST: Total variation
r 2 : = S S R S S T = b 1 2 S S x x S S y y r^2:=\frac{\mathrm{SSR}}{\mathrm{SST}}=\frac{b_1^2 \mathrm{SS}_{x x}}{\mathrm{SS}_{y y}} r 2 : = S S T S S R = S S y y b 1 2 S S x x S S T = ∑ ( y i − y ˉ ) 2 = S S y y S S R = ∑ ( y ^ i − y ˉ ) 2 = b 1 2 S S x x \begin{aligned} & \mathrm{SST}=\sum\left(y_i-\bar{y}\right)^2=\mathrm{SS}_{y y} \\ & \mathrm{SSR}=\sum\left(\hat{y}_i-\bar{y}\right)^2=b_1^2 \mathrm{SS}_{x x} \end{aligned} S S T = ∑ ( y i − y ˉ ) 2 = S S y y S S R = ∑ ( y ^ i − y ˉ ) 2 = b 1 2 S S x x 여기서
∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 = SS x y SS x x \frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}=\frac{\operatorname{SS}_{x y}}{\operatorname{SS}_{x x}} ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) = S S x x S S x y b 1 = ∑ i = 1 n ( x i − x ˉ ) y i SS x x = ∑ i = 1 n k i y i , k i = x i − x ˉ S S x x b_1=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right) y_i}{\operatorname{SS}_{x x}}=\sum_{i=1}^n k_i y_i, \quad k_i=\frac{x_i-\bar{x}}{\mathrm{SS}_{x x}} b 1 = S S x x ∑ i = 1 n ( x i − x ˉ ) y i = i = 1 ∑ n k i y i , k i = S S x x x i − x ˉ
properties related to k i k_i k i
∑ i = 1 n k i = 0 ∑ i = 1 n k i x i = 1 ∑ i = 1 n k i 2 = 1 / S S x x \sum_{i=1}^n k_i=0 \quad \sum_{i=1}^n k_i x_i=1 \quad \sum_{i=1}^n k_i^2=1 / \mathrm{SS}_{x x} i = 1 ∑ n k i = 0 i = 1 ∑ n k i x i = 1 i = 1 ∑ n k i 2 = 1 / S S x x
expectation value of b 1 b_1 b 1
E [ b 1 ] = E [ ∑ i = 1 n k i y i ] = ∑ i = 1 n k i E [ y i ] = ∑ i = 1 n k i ( β 0 + β 1 x i ) = β 0 ∑ i = 1 n k i + β 1 ∑ i = 1 n k i x i = β 1 \mathbb{E}\left[b_1\right]=\mathbb{E}\left[\sum_{i=1}^n k_i y_i\right]=\sum_{i=1}^n k_i \mathbb{E}\left[y_i\right]=\sum_{i=1}^n k_i\left(\beta_0+\beta_1 x_i\right)=\beta_0 \sum_{i=1}^n k_i+\beta_1 \sum_{i=1}^n k_i x_i=\beta_1 E [ b 1 ] = E [ i = 1 ∑ n k i y i ] = i = 1 ∑ n k i E [ y i ] = i = 1 ∑ n k i ( β 0 + β 1 x i ) = β 0 i = 1 ∑ n k i + β 1 i = 1 ∑ n k i x i = β 1
similarly, the variance of b 1 b_1 b 1
V [ b 1 ] = V [ ∑ i = 1 n k i y i ] = ∑ i = 1 n k i 2 V [ y i ] = σ 2 ∑ i = 1 n k i 2 = σ 2 S S x x \left.\mathbb{V} [b_1\right]=\mathbb{V}\left[\sum_{i=1}^n k_i y_i\right]=\sum_{i=1}^n k_i^2 \mathbb{V}\left[y_i\right]=\sigma^2 \sum_{i=1}^n k_i^2=\frac{\sigma^2}{\mathrm{SS}_{x x}} V [ b 1 ] = V [ i = 1 ∑ n k i y i ] = i = 1 ∑ n k i 2 V [ y i ] = σ 2 i = 1 ∑ n k i 2 = S S x x σ 2
Furthermore, recall that the unbiased estimator of σ 2 \sigma^2 σ 2
M S E = S S E n − 2 = ∑ i = 1 n ( y i − y ^ i ) 2 n − 2 = s e 2 \mathrm{MSE}=\frac{\mathrm{SSE}}{n-2}=\frac{\sum_{i=1}^n\left(y_i-\hat{y}_i\right)^2}{n-2}=s_e^2 M S E = n − 2 S S E = n − 2 ∑ i = 1 n ( y i − y ^ i ) 2 = s e 2
Therefore, the unbiased estimator of V [ b 1 ] \mathbb{V} [b_1] V [ b 1 ]
s e 2 S S x x = s e 2 ∑ i = 1 n ( x i − x ˉ ) 2 = s b 1 2 \frac{s_e^2}{\mathrm{SS}_{x x}}=\frac{s_e^2}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}=s_{b_1}^2 S S x x s e 2 = ∑ i = 1 n ( x i − x ˉ ) 2 s e 2 = s b 1 2 Hypothesis Test for the Slope
Step 1.
H 0 : β 1 = 0 H a : β 1 ≠ 0 \begin{aligned} & H_0: \beta_1=0 \\ & H_a: \beta_1 \neq 0 \end{aligned} H 0 : β 1 = 0 H a : β 1 = 0 Step 2.
b 1 − β 1 s b 1 ∼ t n − 2 \frac{b_1-\beta_1}{s_{b_1}} \sim t_{n-2} s b 1 b 1 − β 1 ∼ t n − 2 Step 3.
observed value of t is larger than the critical value
b0
100(1-a)% Confidence Interval
estimate of the average value of y for a given x
V [ y ^ x 0 ] = σ 2 ( 1 n + ( x 0 − x ˉ ) 2 S S x x ) \left.\mathbb{V}[ \hat{y}_{x_0}\right] = \sigma^2\left(\frac{1}{n}+\frac{\left(x_0-\bar{x}\right)^2}{\mathrm{SS}_{x x}}\right) V [ y ^ x 0 ] = σ 2 ( n 1 + S S x x ( x 0 − x ˉ ) 2 ) y ^ x 0 − E [ y x 0 ] s e 1 n + ( x 0 − x ˉ ) 2 S S x x ∼ t n − 2 \frac{\hat{y}_{x_0}-\mathbb{E}\left[y_{x_0}\right]}{s_e \sqrt{\frac{1}{n}+\frac{\left(x_0-\bar{x}\right)^2}{\mathrm{SS}_{x x}}}} \sim t_{n-2} s e n 1 + S S x x ( x 0 − x ˉ ) 2 y ^ x 0 − E [ y x 0 ] ∼ t n − 2 y ^ x 0 ± t α / 2 , n − 2 s e 1 n + ( x 0 − x ˉ ) 2 S S x x \hat{y}_{x_0} \pm t_{\alpha / 2, n-2} s_e \sqrt{\frac{1}{n}+\frac{\left(x_0-\bar{x}\right)^2}{\mathrm{SS}_{x x}}} y ^ x 0 ± t α / 2 , n − 2 s e n 1 + S S x x ( x 0 − x ˉ ) 2 100(1-a)% Prediction Interval
M S E = s 2 2 \mathrm{MSE}=s_2^2 M S E = s 2 2
y ~ x 0 − y ^ x 0 s e 1 + 1 n + ( x 0 − x ˉ ) 2 S S x x ∼ t n − 2 \frac{\tilde{y}_{x_0}-\hat{y}_{x_0}}{s_e \sqrt{1+\frac{1}{n}+\frac{\left(x_0-\bar{x}\right)^2}{\mathrm{SS}_{x x}}}} \sim t_{n-2} s e 1 + n 1 + S S x x ( x 0 − x ˉ ) 2 y ~ x 0 − y ^ x 0 ∼ t n − 2 y ^ x 0 ± t α / 2 , n − 2 S e 1 + 1 n + ( x 0 − x ˉ ) 2 S S x x \hat{y}_{x_0} \pm t_{\alpha / 2, n-2} S_e \sqrt{1+\frac{1}{n}+\frac{\left(x_0-\bar{x}\right)^2}{\mathrm{SS}_{x x}}} y ^ x 0 ± t α / 2 , n − 2 S e 1 + n 1 + S S x x ( x 0 − x ˉ ) 2 Confidence Interval & Prediction Interval
Confidence interval이 Prediction interval보다 얇다.