[Upstage AI Lab] [6주차] AI를 위한 기초수학(1)

🪄 Day 1

✒️ 논리기호 및 정의 기호

• $\forall$ : 모든(All)이라는 표현으로, 기호 뒤에 어떤 조건을 쓰면, 해당 조건의 모든 대상을 가리키는 뜻으로 사용된다
  
• $\exists$ : 대문자 E를 좌우로 뒤집어 놓은 모양으로, 이것도 어떤 조건 앞에 쓰면 그 대상이 존재한다는 의미로 사용된다

🔻 임의성

예를 들어, 부분집합에 대한 정의를 어떻게 서술하는지 살펴보자. 집합 A,B가 주어졌을 때, A가 B의 부분집합(subset)이라고 하는 것은 A의 모든 원소가 다시 B의 원소가 되는 것을 의미한다.

예컨대 A={1,2,3}이고 B={1,2,3,4,5}라면, A의 원소인 세 원소 1,2,3 모두 B의 원소이므로 A는 B의 부분집합이 된다.

이를 위에 적힌 기호를 적용하면..

$\forall x ∈ A, x ∈ B$

A에 있는 어떠한 원소 x를 가져오더라도($x\in A$), 다시 B의 원소가 된다($x\in B$)는 것을 나타낸다.

🔻 존재성

존재성을 이야기해보기 위해 아래와 같은 명제가 있다고 해보자.

There is an integer n such that 3n = 6

이 명제는 참이다. 왜냐면 우리는 n=2인 것을 알고 있기 때문이다. 허나 여기서 명제의 참거짓으로 판단하는 것이 주된 목적이 아니고, 이 문장이 존재성에 대한 문장이라는 것에 주목해야 한다.

만약에 그저 There is an integer n이라고만 했다면, 이는 아무런 의미가 없는 문장일 것이다.

어떤 대상이 존재한다고 하려면, 어떤 조건을 만족하며 존재하는지를 기술해야 하기 때문이다!!

그래서 실제로 존재성에 대한 얘기를 할 때에는 위 문장처럼 "such that"이라고 쓰고 그 이하에 존재하는 조건에 대해서 서술 한다.

기호로 바꿔보면 다음과 같다.

$\exists n\in\mathbb{Z}\text{ s.t. }3n=6.$

• $\mathbb{Z}$ : 정수들의 집합
• s.t. : such that의 줄임말

존재하는 것 중, 유일하게 하나만 존재함을 나타내고 싶을 때는 기존 $\exists$ 옆에 느낌표!를 추가로 붙여서 사용한다.

$\exists !n\in\mathbb{Z}\::\:3n=6$

✔️ 섞여있는 경우 의미 오해하지 않기

하나 주의할 점은 All 기호와 Exist 기호가 섞여 있는 문장이다. 서술을 어떻게 하느냐에 따라 의도가 왜곡될 우려가 있다. 어떤 각 대상"마다" 대응하는 무언가가 "존재"하는지, 혹은 어떤 대상이 "존재"하는 조건으로써 "임의성"을 띄고 있는 조건을 가지는 경우다. 말로만 하면 알아듣기 어렵기 때문에, 두 가지 모두 예시로 파악해보도록 하자.

📍 CASE #1

m=nq+r이라는 식이 있을 때 m과 n이라는 정수 두 개가 임의로 주어질 때마다, 이에 대응하는 몫과 나머지는 유일하게 존재하게 되는 경우를 보자.

예를 들어, m=20,n=7일 때 몫은 2, 나머지가 6이 되는!!

이를 theorem으로써 기술해 둔 것이 나머지정리(Remainder theorem)이라고 한다.

$\text{For every }m,n\in\mathbb{Z} \:(n\neq 0),\text{ there exists a unique integer }q,\:r\text{ with }0\le r<n\text{ such that } m=nq+r.$

각 대상마다 대응하는 무언가가 존재하는 경우에 해당하기 때문에 case로 가져와주셨다.

m,n이 주어질 때마다 적당한 조건을 만족하는 q,r이 존재한다는 것이고, 그렇기에 만약 m,n의 선택이 바뀐다면 이에 맞춰 q,r도 대응하여 바뀔 수 있는 것이다. 숫자 자체가 바뀌어야 한다는 것이 아니라 m,n이 바뀐다면 이 바뀜에 반응을 해야한다는 것을 의미한다!

실제로 논리기호로 정리하면...

$\forall m, n\in\mathbb{Z}\:(n\neq 0),\:\exists!\:q,r\in\mathbb{Z}\:(0\le r<n)\:\text{s.t. }m=nq+r.$

📍 CASE #2

두 번째로는 어떤 대상이 존재하는 조건으로써 임의성을 띄고 있는 경우를 살펴보자.

이때 상계(upper bound)라는 개념이 필요한데, 이는 주어진 집합의 모든 원소보다 큰 값을 의미한다. 혼동할 수 있는 개념으로 상한이라는 것이 있는데, 이는 그러한 상계들 중에서 가장 작은 값을 지칭한다.

만약 실수의 부분집합 A가 아래와 같이 주어졌다고 해보자. 그러면 upper bound가 될 수 있는 것은 아래 사진에서와 같이 M 같은 실수가 될 것이다

만약 "A의 upper bound M이 존재한다"를 upper bound 정의와 함께 풀어쓰면 어떻게 쓸 수 있을까?

$\text{There is }M\in\mathbb{R}\text{ such that }[x\le M\text{ for all }x\in A.]$

여기서의 M이 바로 A의 upper bound가 된다. 즉, M이 A의 upper bound라는 조건 자체가 A의 모든 원소와 비교를 하는 것이기에, M이 존재하는 조건으로써 임의성을 품고 있는 것이다.

논리 기호로 작성하면...

$\exists\:M\in\mathbb{R}\text{ s.t. }[x\le M,\:\forall x\in A.]$

📌 정의기호

어떤 대상을 정의할 때 사용하는 기호를 알아보자

• A : 정의하고자 하는 대상 → unknown
• B : 아는 대상 → known

이라고 한다면 A를 B로 정의한다는 표현은 다음과 같다.

$A\coloneqq B$

보다시피 클론이 있는 부분이 unknown feature가 된다. 영어 문장으로는 "A is defined by B"라고 쓸 수 있다

✒️ Subset and Power set

📌 Subset

먼저 object와 sub-object의 개념을 예시와 함께 생각해보자. 냉장고라는 object가 있다고 했을 때 내장고엗 여러 브랜드가 있고, 또 각 브랜드마다 여러 냉장고 모델이 있을 것이다. 우리는 그 모두를 냉장고라고 칭하는데, 각 브랜드별 각 제품 모델이 sub-object에 해당한다고 보면 된다.

즉, 우리가 실제로 다루는 것은 냉장고라는 추상적 개념이 아니라 냉장고로서의 기능 및 특징을 갖추고 있는 실제 모델인 것이다!

이제 부분집합(Subset)을 살펴보자

• 부분집합 (Subset) : 특정 집합의 일부를 원소로 가지고 있는 집합으로, A가 B의 부분집합이라고 했을 때 A의 모든 원소가 B의 원소임을 만족하는 집합
  • 수식 : $\forall x\in A,\:x\in B$
  • 진부분집합(proper subset) : $A\subset B$ 이면서 $A\neq B$ 인 경우
  • super set : $A\subset B$ 일때 A를 B의 부분집합이라고도 하지만, B를 A의 super set이라고도 함

• 상등 : 집합 A,B가 같다는 것으로, double inclusion이 만족할 때를 의미한다
  • 즉, 두 집합이 같다는 것은, 서로가 서로를 포함하는 관계가 성립할 때를 의미하는 것!
  • 수식 : $A=B\Longleftrightarrow A\subset B, A\supset B$

📌 Power Set

집합 A가 주어졌을 때, A의 부분집합으로 최소 자기 자신과 공집합은 보장되어 있음을 알 수 있다! 그런데 일반적으로는 더 많은 부분집합이 있을 수 있을 것이다!

이러한 A의 모든 부분집합을 모아놓은 집합을 A의 power set이라고 하고 기호로는 $\mathcal{P}(A)$ 라고 쓴다

$\mathcal{P}(A)\coloneqq\{B\::\:B\subset A\}$

즉, A가 무슨 집합이든 상관없이, $A\in\mathcal{P}(A)$이고 $\emptyset\in\mathcal{P}(A)$인 것이다.

여기서 원소 포함기호인 $\in$이 쓰인 것에 주목해야하는데, $A$는 집합이지만, $\mathcal{P}(A)$와의 관계에서는 $A$는 $\mathcal{P}(A)$의 원소이다. 즉, 집합-원소 관계는 지극히 상대적인 것임을 유의할 것!

✒️ Basic Set Operations

📌 Union

• 합집합 $A\cup B$ : $A\cup B\coloneqq\{x\in X\::\: x\in A\text{ or }x\in B\}$

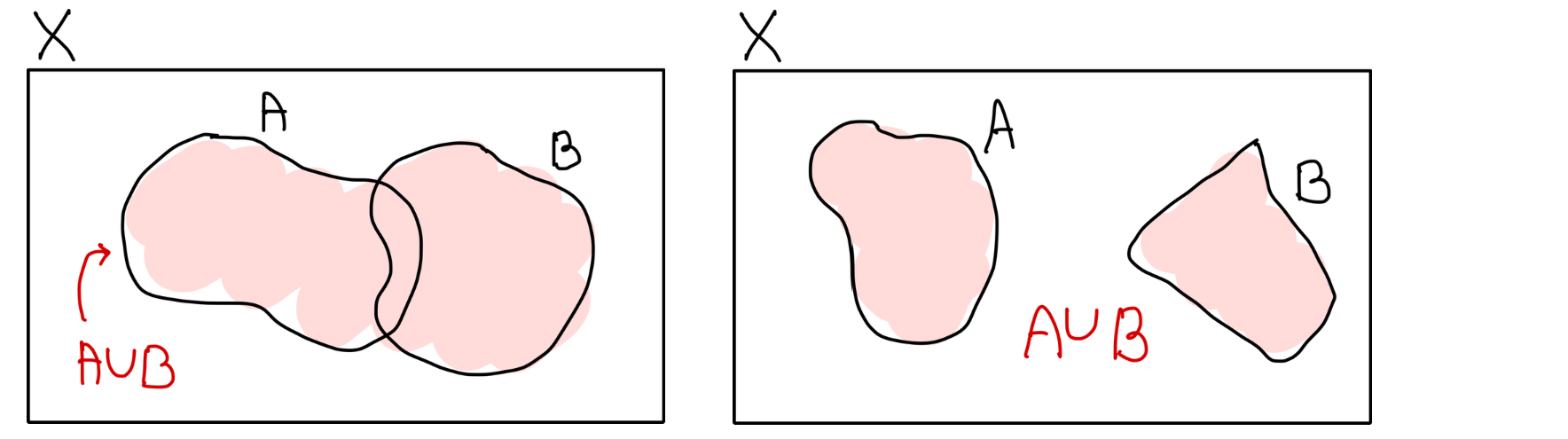
📌 Intersection

• 교집합 $A\cap B$ : 두 집합 모두에 속하는 원소만을 모아놓은 것
  - $A\cap B\coloneqq\{x\in X\::\:x\in A\text{ and }x\in B\}$
  

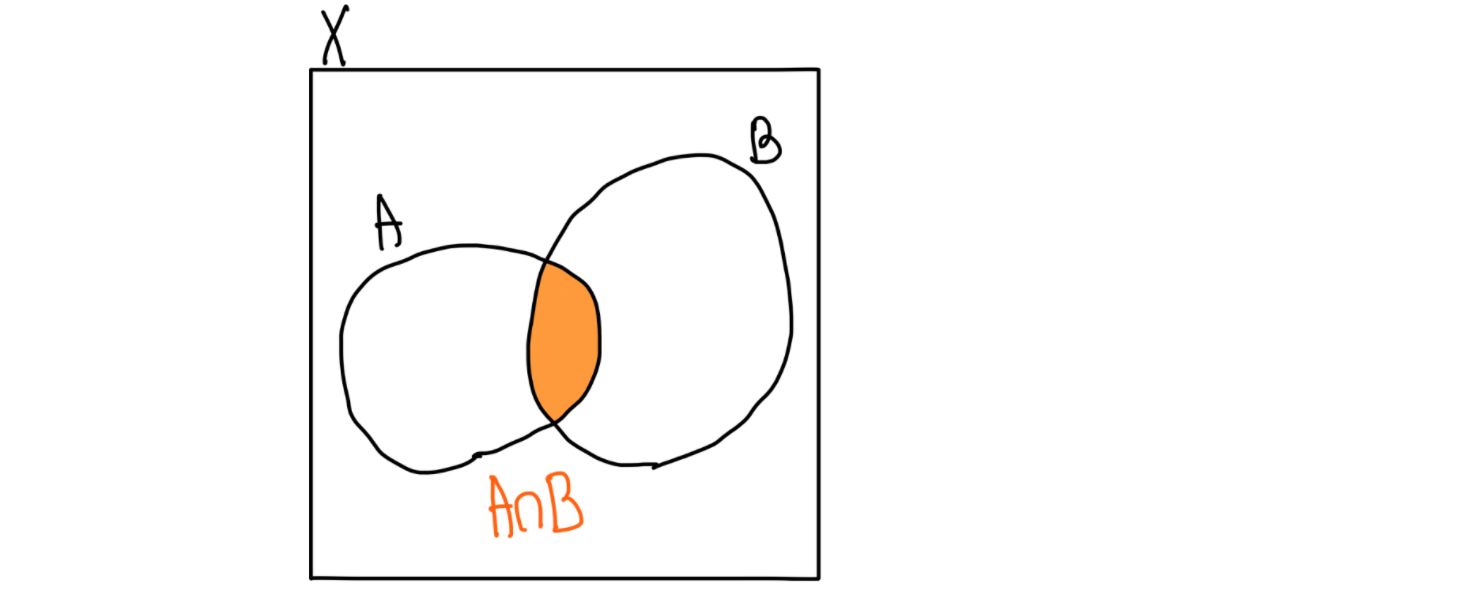
📌 Set Minus

• 차집합
  $A\setminus B$ : 두 집합 간의 차이를 구하는 것
  - $A\setminus B\coloneqq \{x\in X\::\:x\in A\text{ and }x\notin B\}$

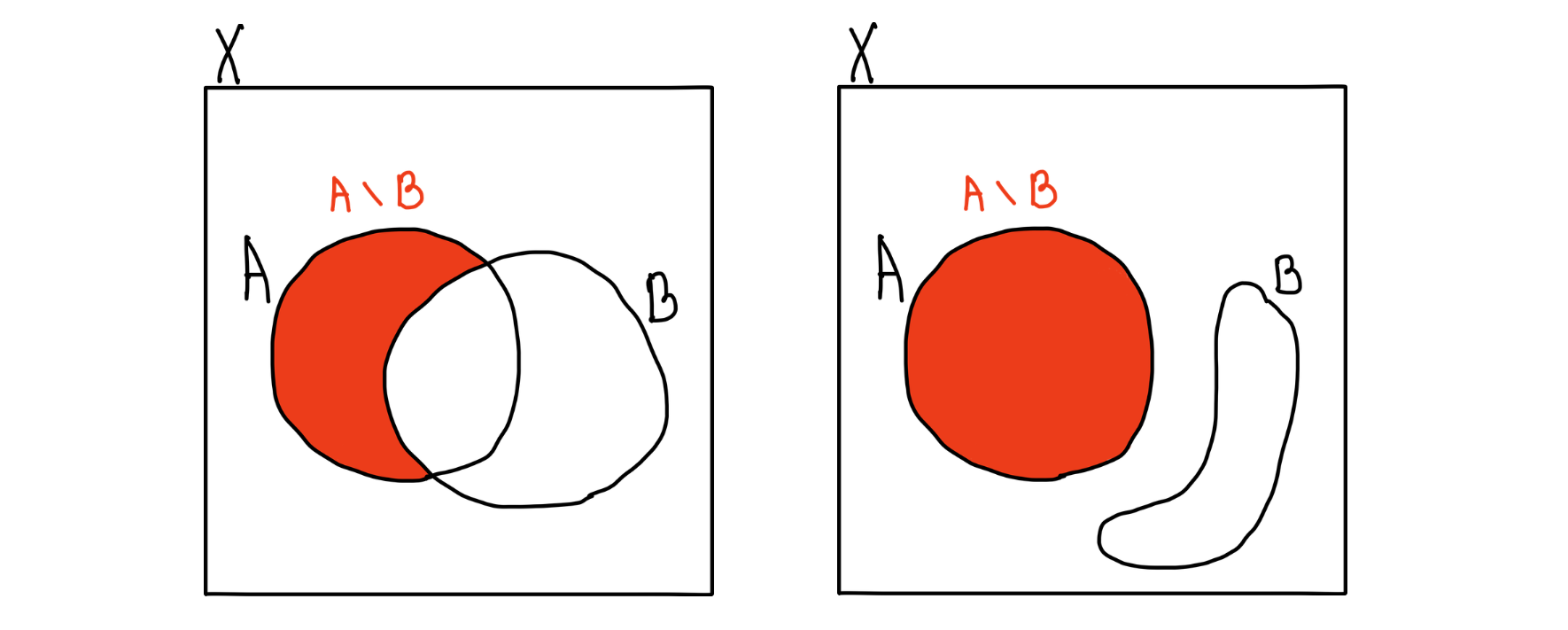
📌 Completion

• 여집합 $A^c$ : 특정 집합 외의 것
  - $A^c\coloneqq X\setminus A$

📌 Cartesian Product

• 집합곱 $A\times B$: 순서쌍의 모임
  - $A\times B\coloneqq\{(a,b)\::\:a\in A,\:b\in B\}$
  

이때 순서쌍은 순서에서 유의를 해야한다.
예) $(1,2)\neq (2,1)$

$\mathbb{Z}\times\mathbb{Z}=\mathbb{Z}$ (X)

원소를 대입해서 순서쌍을 구성하기 때문에, 일반적으로 $A\times B\neq B\times A$가 성립한다

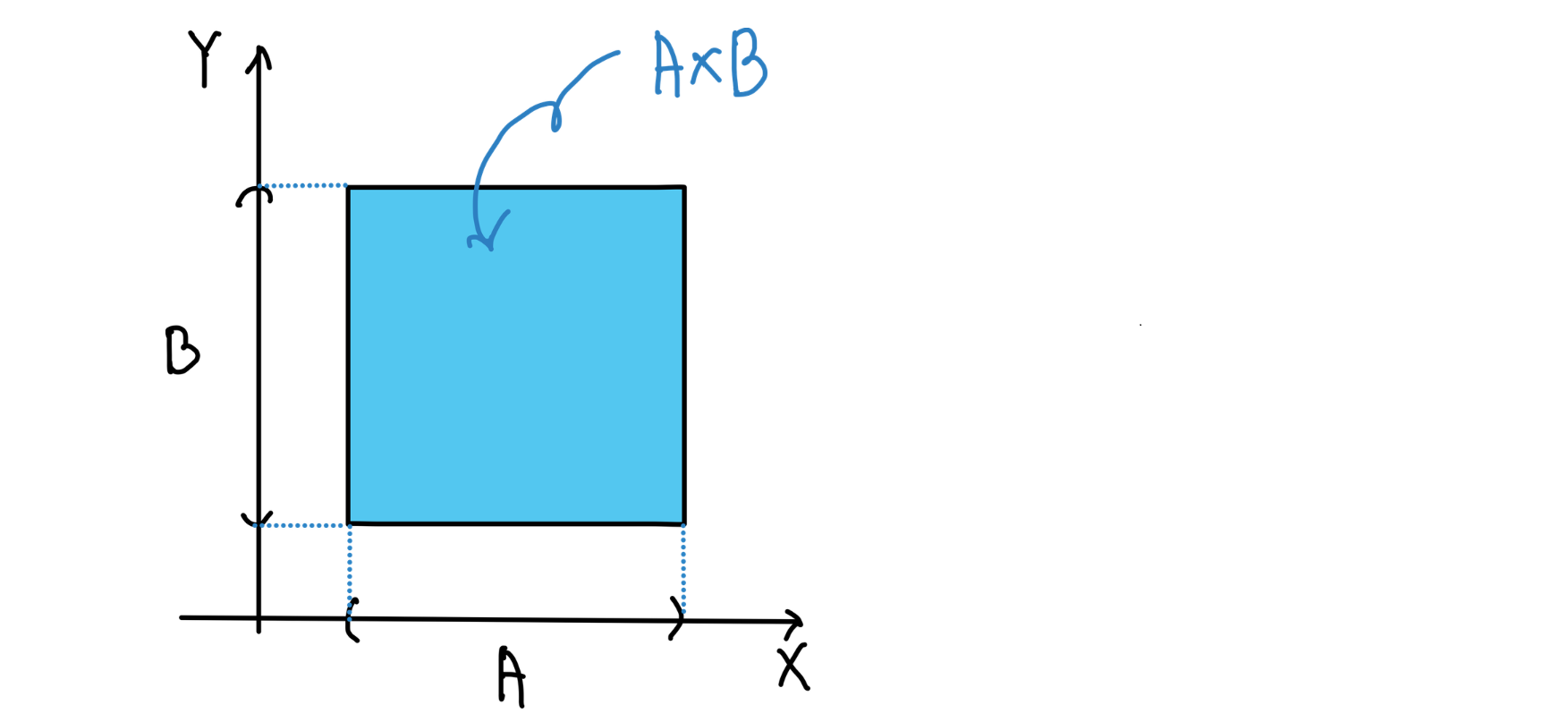
✒️ Statement and Logical Operations

📌 Statement / Condition

• 명제(Statement) : 명확히 참이나 거짓을 판단할 수 있는 문장을 뜻함
  • 명제 예시 : 1은 자연수이다(참), -1인 자연수이다(거짓)
  • 명제가 아닌 예시 : 꽃은 아름답다 (참,거짓을 따질 수 있는 문장이 아니기 때문)

• 조건 (Condition) : 명제 중에서 미지수에 의해 참, 거짓이 판별될 수 있는 명제를 의미
  • 가령, 집합 A에 대하여 $x\in A$라고 하는 명제는 x가 무엇이냐에 따라 참일 수도 있고 거짓일 수도 있기 때문에 조건에 해당

📌 Logical Operations

두 조건 p,q가 주어졌을 때

📍 AND

• AND $p\land q$ : 두 조건 모두 TRUE일 때에만 TRUE인 조건

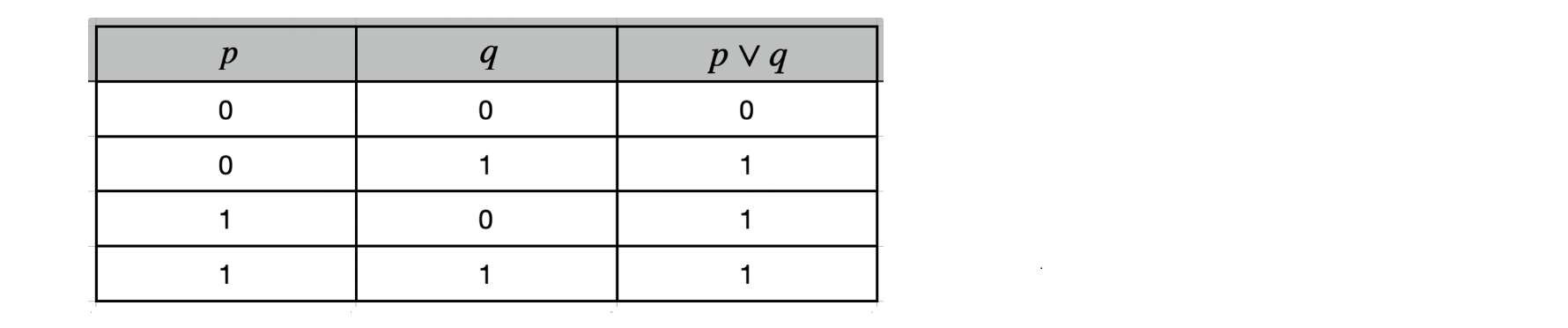
📍 OR

• OR $p\lor q$ : 두 조건 중 적어도 하나가 TRUE일 때 TRUE인 조건

📍 NOT

• NOT $\neg p$ : p가 TRUE면 FALSE로, FALSE면 TRUE인 조건

📍 implications

• 내포(implications) $p\rightarrow q$ : p가 TRUE면 FALSE로,
  • p는 가정, q는 결론이라고 부름
  • $p\rightarrow q$가 갖는 의미
    • 가정이 거짓인 경우 : 결론과 상관없이 $p\rightarrow q$ 자체가 참
    • 가정이 참인 경우 : 결론이 참일 때만 $p\rightarrow q$가 참이 됨

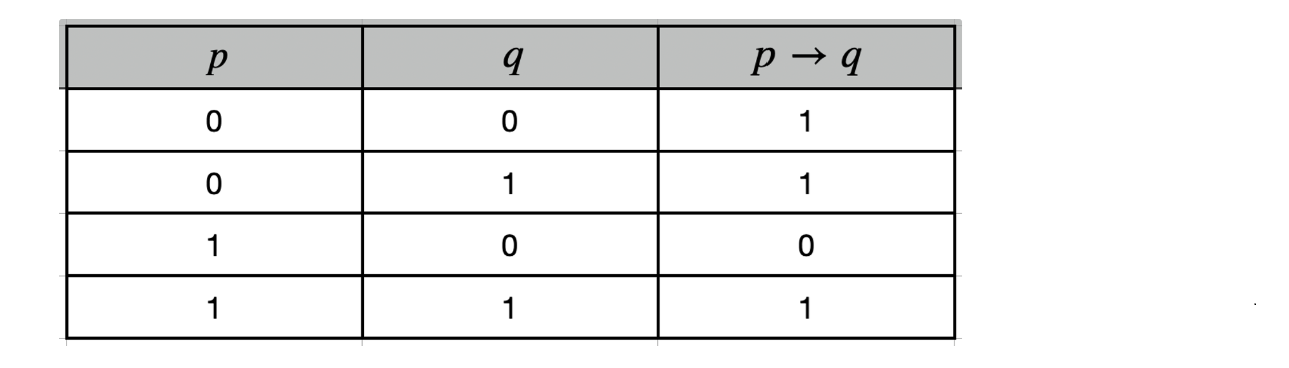
가정 p가 거짓인 경우를 살펴보자. 특별한 경우로 $p\rightarrow p$ 라는 명제를 생각해보자. p가 거짓이든 참이든 다음 명제가 참이 된다는 것은 쉽게 이해할 수 있을 것이다. 이런 논리 하에 가정 p가 거짓인 경우엔 결론 q의 참거짓 여부와 상관없이 $p\rightarrow p$ 는 참으로 정의를 하는 것이다. 이와 같이 가정이 거짓일 때 전체 명제가 참이 되는 것을 vacuous truth, 혹은 vacuously true라고 부른다.

• 반례 (couter-example) : 명제가 틀렸다는 것을 보이기 위함
• 대우명제 (contrapositive statement) : $p\rightarrow q$ 이면 $\neg q\rightarrow \neg p$ 이다

🔻 진리집합 (Truth Set)

• 진리집합(Truth Set) : 조건을 참으로 만드는 값들을 모아놓은 집합

$p, q$의 진리집합을 각각 $P,Q$라고 해보자. 앞서 다뤘던 것처럼 $p\rightarrow q$가 참이라는 것은 $p$가 거짓이거나, $p$가 참일 때 $q$ 또한 참인 경우를 의미한다.

이때, $p,q$는 조건이기 때문에 정확히는 미지수를 같이 고려해야 한다! 예를 들어,

이라고 하면, $p(x)\rightarrow q(x)$는 참이다.

when? 👉 $p(x)$를 참으로 만드는 모든 $x$에 대해서! 즉, 가정을 참으로 만드는 모든 $x$에 대해서 $p(x)\rightarrow q(x)$가 참인 것이다.

당연히 $p(x)$를 거짓으로 만드는 $x$를 가지고 오더라도 $q(x)$의 참거짓 여부와 관계없이 $p(x)\rightarrow q(x)$ 자체는 참인 것이다. 이 경우 진리집합은

가 된다. 따라서 $p\rightarrow q$가 참이면 $P\subset Q$가 성립하게 된다.

🔻 충분조건 (sufficient condition) 과 필요조건 (necessary condition)

• $p\rightarrow q$가 참이라 가정

진리집합 간의 포함관계는 $P\subset Q$가 된다. 그림으로는 P가 Q에 쏙 들어가 있는 모습일 것이다.

이 경우 p는 q이기 위한 충분조건
q는 p이기 위한 필요조건이라고 부른다.

• $p\rightarrow q$가 참이면서 동시에 $q\rightarrow p$가 참

이러면 p는 q이기 위한 충분조건이자 필요조건까지 되는 것!

p와 q는 서로 필요충분조건(necessary and sufficient condition)이 된다. 기호로는 $p\leftrightarrow q$ 라고 쓰며, 영어로는 if and only if, 줄여서는 iff로도 작성한다!

✒️ Relations and Functions

📌 Relations

개념
집합 $A,B$가 주어져 있을 때, 부분집합 $R\subset A\times B$을 $A$와 $B$의 관계(Relation)라고 부른다.

$(x,y)\in R$ 이 있을 때에는 $x$가 $y$에 $R$-related 되어있다고 하며, 기호로는 $xRy$로 표기하도록 하겠다.

이렇게 정의한 relation $R$에 대하여 $A$를 정의역(domain), $B$를 공역(codomain)이라고 부른다.

Relation $R\subset A\times B$가 주어져 있을 때, 주어지는 조건에 따라 여러 이름이 붙는데, 한 번 살펴봅세~

📍 functional

R이 functional하다는 것은
$xRy, xRz\Longrightarrow y=z$을 만족할 때를 의미한다

👉 하나의 입력에 대해 하나의 출력만 가짐

ex. 만약 R가 학생과 학번의 관계라면, 각 학생은 유일한 학번을 가져야 하므로 이 관계는 함수적이다

📍 injective

R이 injective하다는 것은
$xRz,yRz\Longrightarrow x=y$을 만족할 때를 의미한다

👉서로 다른 입력이 서로 다른 출력을 가짐

ex. 만약 학생의 학번과 이메일 주소의 관계가 있다면, 각 학번에 대해 유일한 이메일 주소가 있어야 하며, 서로 다른 학번에 대해 동일한 이메일 주소가 지정되지 않는다면 이 관계는 단사적이다.

📍 surjective

R이 surjective하다는 것은
$\forall y\in B,\:\exists x\in A\text{ s.t. }xRy$을 만족할 때를 의미한다

👉모든 출력에 적어도 하나의 입력이 대응됨

ex. 학생과 학번의 관계가 있다면 모든 학번은 반드시 한 학생과 관련이 있어야 한다. 그렇지 않으면 그 학번은 전사적이지 않다고 할 수 있다.

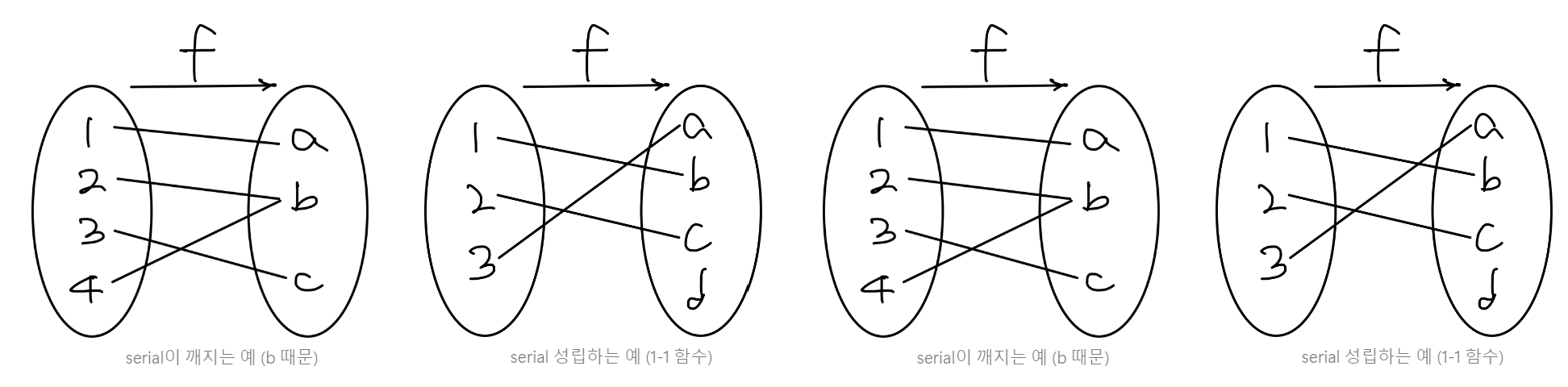
📍 serial

R이 serial하다는 것은
$\forall x\in A,\:\exists y\in B\text{ s.t. }xRy$을 만족할 때를 의미한다

👉 모든 입력이 적어도 하나의 출력과 관계를 가짐

ex.학생과 수강한 과목의 관계에서, 모든 학생이 적어도 하나의 과목을 수ㅏㅇ해야 한다면 이 관계는 전계적이다.

📌 Functions

$f\subset A\times B$

집합 $A,B$가 주어져 있을 때, 함수(Function) $f:A\rightarrow B$는 아래의 두 조건을 만족시키는 $A$와 $B$에 대한 관계(Relation)이다 :

1. $f$는 functional,
2. $f$는 serial.

📍 1-1, one-to-one, injective, 단사

• $f(x_1)=f(x_2)\Longrightarrow x_1=x_2$

출력값이 같다면 입력값도 반드시 같아야 하는 함수다. 따라서 함숫값이 하나일 때, 그 함숫값을 만드는 입력값(즉, 함수의 인자)은 하나뿐이라는 의미!

예를 들어, 두 사람이 같은 결과를 얻는다면, 그들은 같은 방법(입력값)을 사용한 것이다! 어떤 두 개의 입력이 동일한 출력을 낳을 수 없다면, 그 함수는 단사적이라고 할 수 있다. 즉, 같은 결과값이 있다면, 그건 같은 입력값에서 나온 것!

📍 onto Function (surjective, 전사)

• $\forall y\in B,\:\exists x\in A\::\:y=f(x)$

함수의 모든 출력값이 반드시 사용되는 함수를 의미한다. 즉, 함수의 출력값들이 포함된 집합인 '공역'의 모든 원소가, 적어도 하나의 입력값과 연결되어야 있어야 한다.

전사함수는 치역과 공역이 동일하고, 모든 원소가 사용되어 '모든 가능성을 커버하는 함수'라고 생각할 수 있다.

📍 Correspondence (bijective, 전단사, 일대일대응)

• $\forall y\in B,\:\exists! x\in A\::\:y=f(x)$

일대일대응 함수는 입력과 출력이 정화깋 하나씩 짝지어지는 함수다. 단사(injective), 전사(surjective) 성질을 가지고 있어, 입력 값마다 하나의 출력 값이 대응하고 출력 집합의 모든 값이 입력 집합의 어떤 값과 연결되어 있다는 뜻이다.

📍 Inverse Function (역함수)

• $f^{-1}(y)\coloneqq x\text{ where }y=f(x)$

$f^{-1}$ 는 $y=f(x)$인 원소 y에 대해 그에 대응하는 $x$를 찾아내는 함수다. 역함수가 제대로 정의되기 위해서는 원래 함수 f가 일대일대응 함수여야 한다. 이 조건이 충족되면,f의 모든 출력 y는 고유한 입력 x를 갖고, 따라서 역함수가 명확하게 정의된다.

역함수가 "잘 정의된다"는 것은, B의 모든 원소에 대해 오직 하나의 A의 원소가 대응한다는 것이다. 이 말은 역함수가 혼란 없이 정확하게 동작한다는 뜻이다.

📍 Composition Function (합성함수)

• $(g\circ f)(x)\coloneqq g(f(x))$

합성함수는 두 함수를 연속해서 적용하는 함수로, 한 함수의 출력이 달느 함수의 입력이 되는 방식으로 두 함수를 결합한 것이다.

📍 Identity Function (항등함수)

• $id_A:A\rightarrow A$ defined by $id_A(x)\coloneqq x$

항등함수는 입력값을 그대로 출력하는 함수!

🔻 원함수와 역함수와의 관계

• 원함수와 역함수의 합성함수는 항등함수다!
• 원함수와 역함수는 $y=x$ 대칭이다!

✒️ Binomial Theorem

• Factorial : $n\in\mathbb{N}$에 대하여, Factorial $n!$은 다음과 같이 정의되는 수

  • $n!\coloneqq\prod_{1\le m\le n}m\coloneqq n\times (n-1)\times\cdots\times 2\times 1$
  • $0!\coloneqq 1$로 정의

• 이항계수 (Binomial Coefficient) : $n,r\in\mathbb{N}\cup\{0\},\:0\le r\le n$에 대하여

  • $\begin{pmatrix} n \\ r \end{pmatrix}\coloneqq\frac{n!}{r!(n-r)!}$

• 이항정리 (Binomial Theorem) : 두 개의 항으로 구성된 식을 전개하는 방법을 정리한 것

  • $(a+b)^n=\sum_{r=0}^n\begin{pmatrix}n\\r\end{pmatrix}a^r b^{n-r}$
  • $(a+b)^2=(a+b)(a+b)=1\cdot a^2+2\cdot ab+1\cdot b^2=\begin{pmatrix}2\\0\end{pmatrix}a^2+\begin{pmatrix}2\\1\end{pmatrix}ab+\begin{pmatrix}2\\2\end{pmatrix}b^2$