본 포스트는 고려대학교 강필성 교수님의 강의를 수강 후 정리를 한 것입니다. 작성 및 설명의 편의를 위해 아래 포스트는 반말로 작성한 점 양해부탁드립니다.

Abnormal Data란

• Anomaly Data는 다음과 같이 Hawkins와 Harmeling에 의해 정의된다.

Observations that deviate so much from other observations as to arouse suspicions that they were generated by a different mechanism. – Hawkins, 1908

Instances that their true probability density is very low. – Harmeling et al, 2006

• 다시 한번 정리해보자면, 이상치 탐지는 기존 데이터들과 생성되는 매커니즘이 다르거나 발생 빈도가 낮은 데이터를 의미한다.

• 그렇다면, 이상치 탐지가 일반적인 우리가 딥러닝/머신러닝에서 수행하는 Binary Classification과는 어떤 차이가 있을까?

1. 학습 방법론 관점

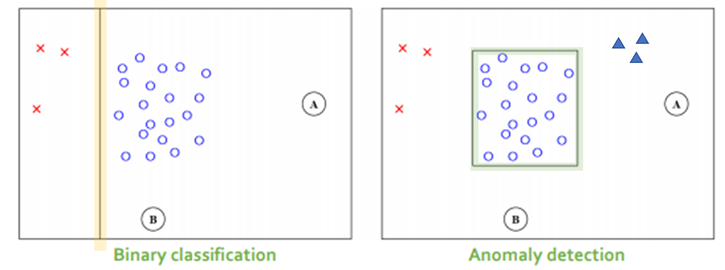
• Binary Classification: 정상과 비정상을 구분하는 분류경계면(선)을 학습하여 이를 기준으로 정상과 비정상을 나눈다. (A, B – 정상)
• Anomaly Detection: 이상치란 한가지 종류만 있는 것이 아니다. 예를 들어 x와 ▲를 이상치라고 하자. 이 둘 이상치 모두 수가 적어 이상치를 대표하지 못하기 때문에 같은 이상치라고 binary하게 정의를 내려줄 수 없다. 때문에 이상치 탐지에서는 정상데이터를 가지고 정상 영역을 추정하고 그 외의 영역에 속하는 값들을 정상이 아니라고 판단한다. (A, B – 비정상)

2. 학습 데이터 관점

• Anomaly Detection은 기본적으로 “정상” 데이터가 “비정상” 데이터보다 훨씬 더 많다는 것을 가정하고 있다.
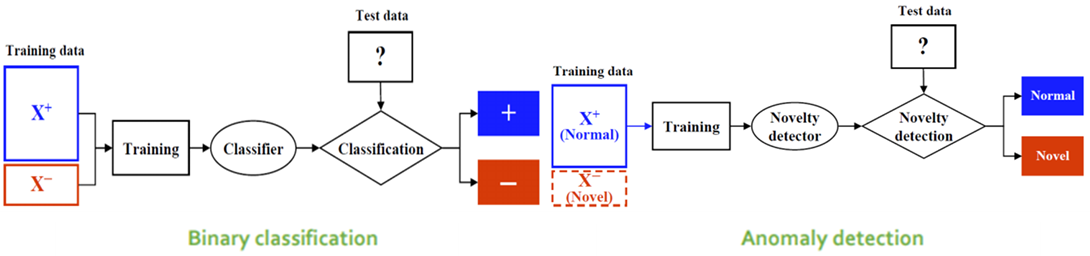
• Binary Classification: 정상과 비정상(이상치) 데이터를 모두 이용하여 학습을 수행한다.
• Anomaly Detection: 비정상(이상치) 데이터를 제외한 정상 데이터만을 가지고 학습을 수행한다.
  

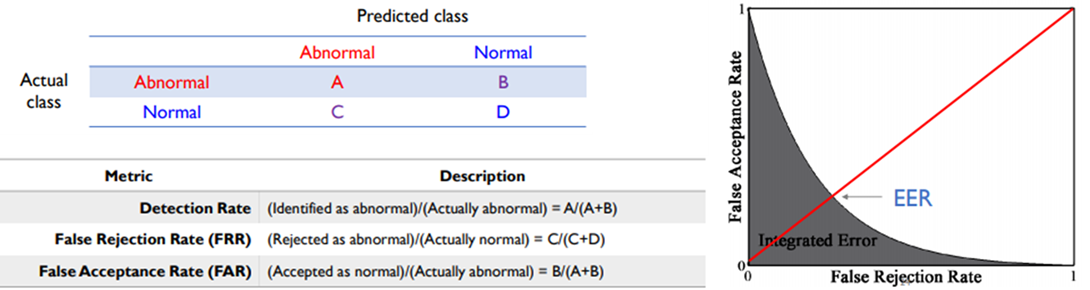
3. 평가 방법 관점

밀도 기반 이상치 탐지

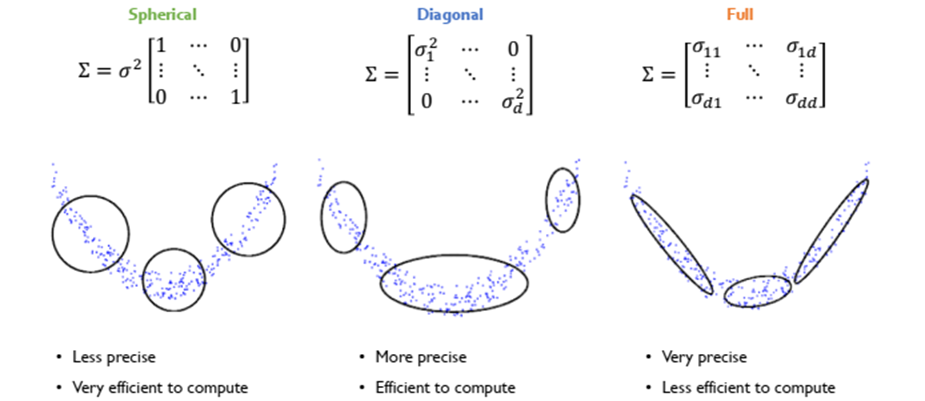
• 정상 데이터의 데이터 분포를 사용하여 정상 상태의 분포를 추정한 뒤, 새로운 객체에 대하여 확률이 높으면 정상, 확률이 낮으면 비정상을 반환하는 방법론이다. 일반적으로 데이터의 분포를 설명하는 모수 모형(Parametric Model을 가정하며, 정규 분포로 추정을 할 때 몇 개의 가우시안 모델이 사용되었는가에 따라 다음과 같이 분류될 수 있다.

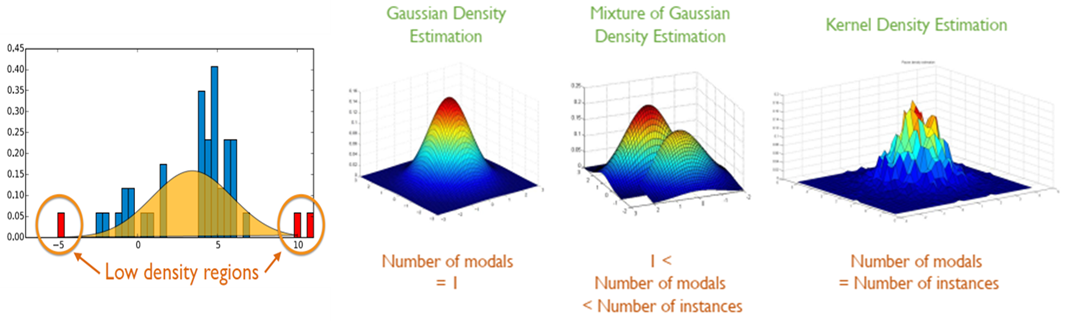
Gaussian Density Estimation

• 가정
  - 관측치들은 하나의 Gaussian으로부터 생성되었다.
  

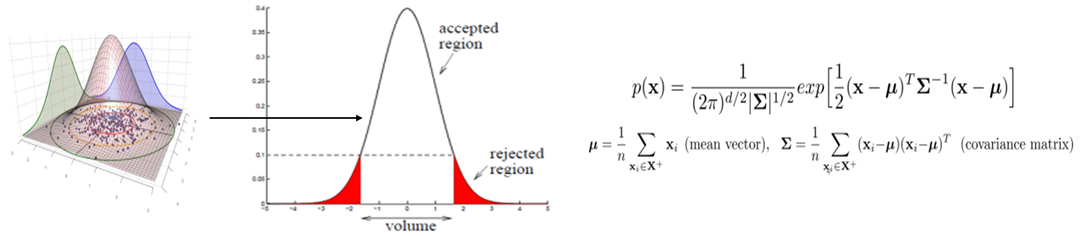
• 장점
  1. 데이터의 범위에 민감하지 않다. (∵ 공분산 행렬은 측정 단위가 영향을 끼치지 않음)

  2. 분포를 추정한 학습데이터로부터 처음부터 rejection에 대한 1종 오류를 정의할 수 있다. (ex. 신뢰수준 95%)

• Formulation (Parameter estimation: $μ$, $σ^2$)

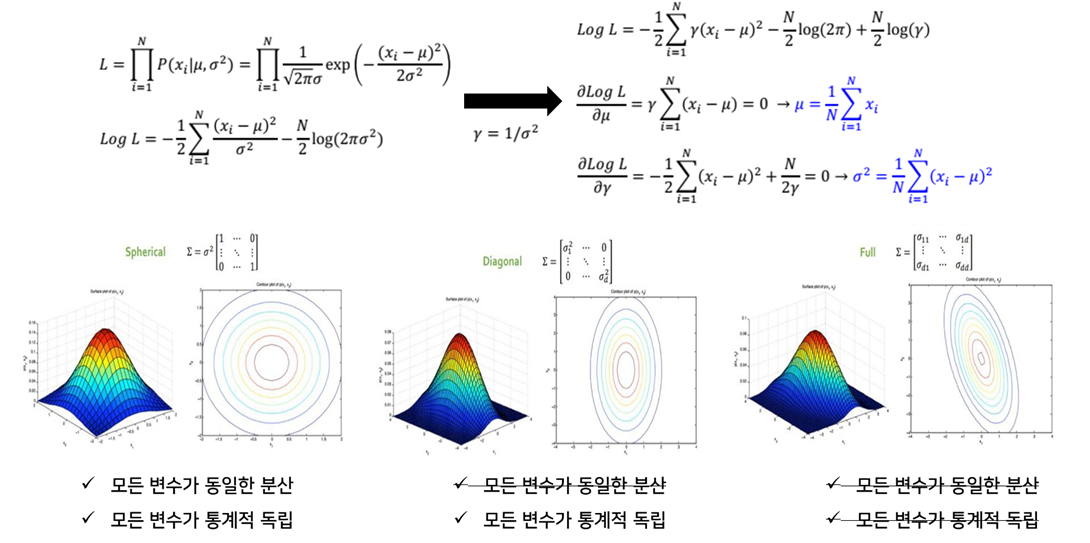
Mixture of Gaussian Density Estimation

• 가정
  - 관측치들은 여러 개의 Gaussian들의 선형결합으로부터 생성되었다.
  

• 가우시안 결합 모델과 각각의 가우시안 모델(수식)
  

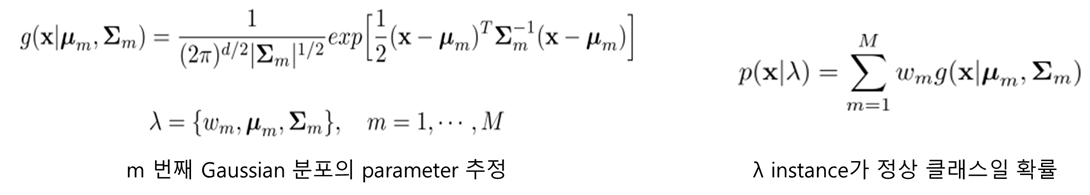
• Formulation (Parameter estimation: $μ_m$, $w_m$, $Σ_m$)
  - EM 알고리즘을 사용하여 구할 수 있다.
  
  

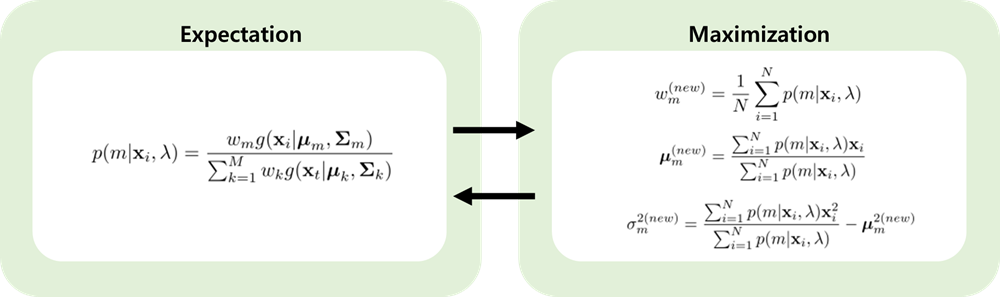
Kernel Density Estimation

• 이전 Gaussian Density Estimation과 Mixture of Gaussian Density Estimation에서는 특정 분포를 가정하고, 파라미터를 예측하는 parametric approach였다.
• Kernel Density Estimation은 non-parametric approach로, 분포를 예측하지 않고 데이터 자체를 이용해서 밀도를 추정하고자 한다.
• 분포 p(x)에서 추출한 벡터 x가 표본 공간의 주어진 영역 R에 포함될 확률을 P라고 하면 다음과 같은 식을 구할 수 있다.
  
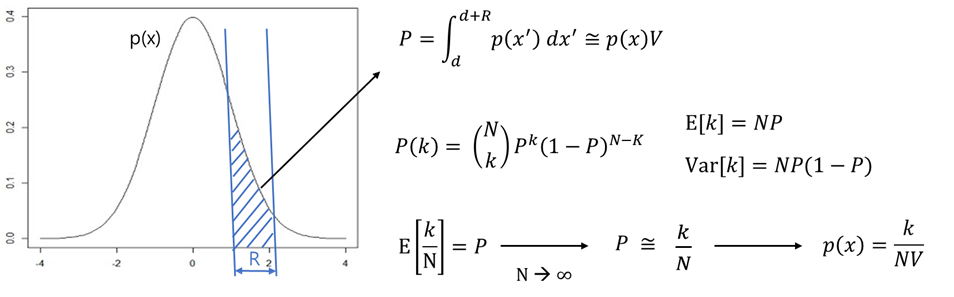
• 아래 식에서 V를 고정하고 k를 찾아주는 것이 Kernel-density Estimation의 주요 아이디어이며, Parzen Window Density Estimation은 Kernel-density Estimation의 대표적인 방법 중에 하나이다.
  

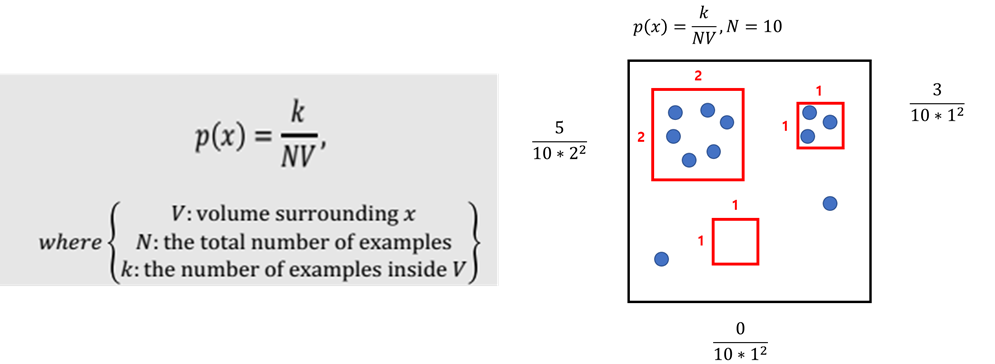
Parzen Window Density Estimation

• Parzen Window Density Estimation에서는 데이터가 d차원 공간(V = hd) 안에 있는 샘플의 개수를 세는 방식으로 밀도를 추정하게 된다.
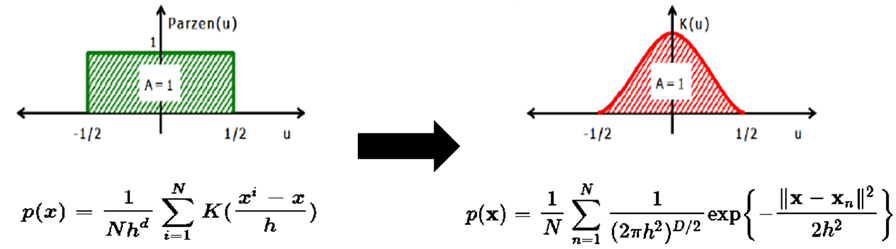
• 밑의 K(u)식은 해당 공간 안에 샘플(X)가 들어오면 1을 반환하는 함수이고, k는 해당 공간안에 있는 샘플의 수를 의미한다. 이와 같은 K는 커널 함수의 일종이며 파젠 윈도우(Parzen Window)라고 한다. 이를 통하여 데이터의 확률 밀도 함수를 아래와 같이 구할 수 있다.
  
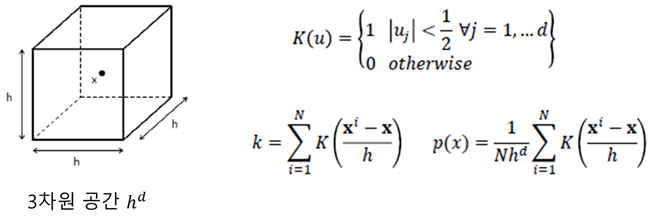
• 하지만, 위의 K(u)함수는 영역 안이면 1, 밖이면 0을 부여하게 됨으로 큐브의 기장자리 영역에서 불연속성을 갖게 되고, uniform distribution이기 때문에 거리가 달라도 모두 같은 가중치가 곱해진다는 단점이 있다.
• 이를 극복하기 위해 개별적인 객체를 가우시안 분포의 중심으로 보고 확률밀도함수를 계산해주는 smoothing을 취해줄 수 있다.
  
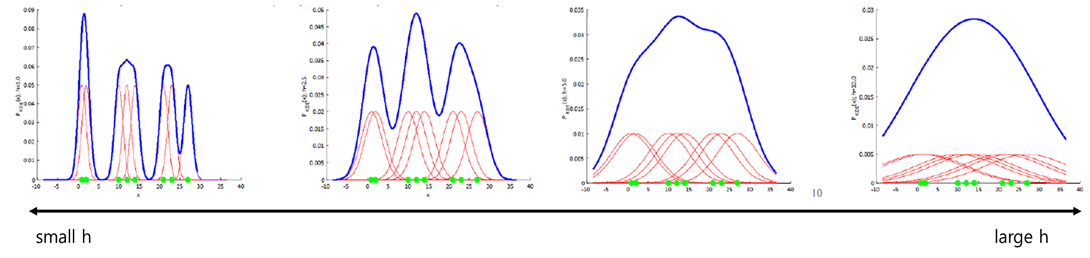
• 이때 smoothing parameter h를 너무 작게 잡아주면 뾰족뾰족하게 under-smoothing한 형태를 보이고, h를 너무 크게 잡아주면 두루뭉술하게 over-smoothing한 형태를 보인다.
  

Local Outlier Factor (LOF)

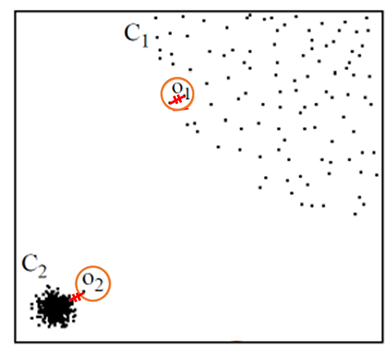
• 아래 Cluster1과 Cluster2에서 각각의 점 O1, O2는 같은 거리만큼 떨어져 있다. 과연 어느 점을 이상치라고 할 수 있을까? 단순히 거리만을 비교해보면 각각의 군집에서 객체들은 같은 거리만큼 떨어져 있으므로 같다고 판단되겠지만, 우리는 그러한 값을 원하지 않는다.
  

• Local Outlier Factor(LOF)의 목적 : 우리는 O2의 abnormal score가 O1의 abnormal score보다 크게 측정이 되길 원한다.

• LOF를 알기 위해서는 다음 5가지 개념의 거리에 대해서 알아야 한다.
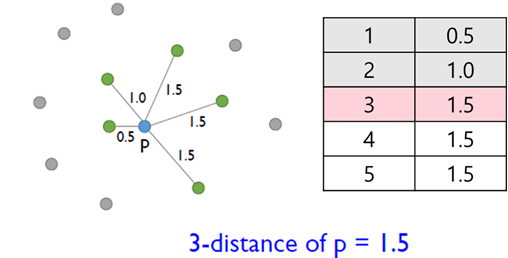
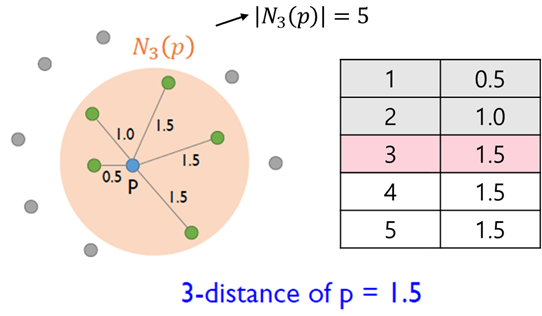
  ① k-distance(p)

• 객체 p로부터 k번째 근접 이웃까지의 거리
  

② Nk(p)

• k-distance(p) 안에 들어오는 object의 집합
  

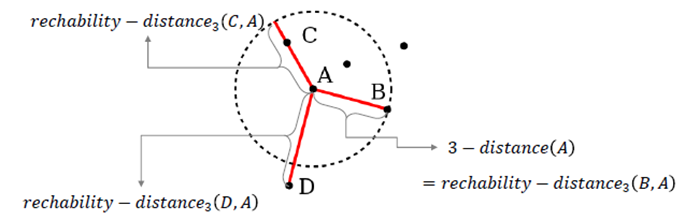
③ reachability-distancek(p,o)

• max{k-distance(o), d(p,o)}, 이웃 o를 기준으로 k-distance(o)와 d(p,o)사이의 max 값을 반환한다. 이 작업을 통해 k-distance 안 쪽에 있는 이웃들의 거리를 k-distance 거리로 치환해주게 된다.
  

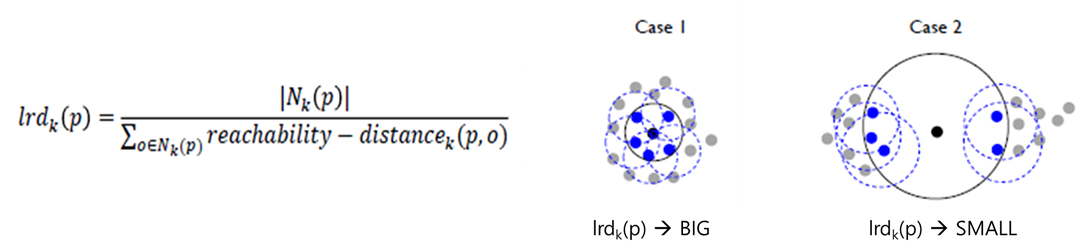
④ lrdk(p)

• local reachability density of an object p, 객체 p를 기준으로 했을 때 local density distance.
  

⑤ LOFk(p)

• local outlier factor of an object p
  

• 단점

  1. 계산 복잡도가 높다.
  2. Score 값이 normalize되지않아 다른 데이터 셋과의 비교가 불가능하다.

다음 포스트는 거리/군집/서포트벡터 기반 이상치탐지 기법들로 찾아뵙겠습니다.

긴 글 읽어주셔서 감사합니다 ^~^