■ Evaluating and Choosing the Best Hypothesis(가설 평가와 선택)
■ Model Selection(모델 선택)

-
Supervised Learning = Finding the best hypothesis
-모델 선택: define the hypothesis space(지식의 모양과 차수를 사람이 정해줌)
-파라미터 결정: 학습 데이터와의 오차를 줄이는 방향으로 최적화된 파라미터 값을 결정해가는 알고리즘(가설 함수를 확정시킴)
-사람이 많이 개입할수록 알고리즘의 부담이 낮아짐 -
Model complexity(모델 복잡도)
-Parameter size(매개변수 개수) 증가
-훈련 데이터의 양과 학습 시간 모두 증가
-매개변수의 개수가 증가하는데 훈련 데이터가 적으면 최적의 값을 결정할 수 없음
-설계자가 model selection 부분을 잘 정해줘야 함
■ Evaluating Hypothesis(가설 평가)

-Validation set(검증 집합): traning set(훈련 집합), validation set(검증 집합) -> 훈련집합과 모양은 똑같음 / 내용면에서는 훈련집합과 다름(검증이 목적), test set(테스트 집합) / 검증 집합과 테스트 집합은 거의 혼용해서 사용
- Cross-Validation(교차 검증)

-validation은 학습 데이터에 있지 않는 또다른 데이터로 검증을 의미
-Holdout cross-validation: 데이터가 충분히 많을 때
-k-fold cross-validation: k가 10이라고 가정, 1fold가 100이라고 가정, 900은 훈련 데이터 / 100을 검정 데이터로 사용하고 난 후 역할을 바꿔서 900개가 검정 데이터, 100을 훈련 데이터로 사용 - 이렇게 1000개의 데이터가 있고 k-fold가 10일 때 10번 진행되고 이를 다 진행한 후에 평균을 내서 평균 성능을 최종 성능으로 보게 됨
-leave-one-out cross-validation: 데이터가 n개가 있으면 한 개만 남기고 나머지는 다 학습에 사용(데이터가 극단적으로 적을 때) ex) 데이터가 10개일 때 테스트 데이터 한 개만 남기고 나머지 9개를 훈련 데이터(학습 데이터)로 사용 -> 10번 진행하게 됨
■ Error Rates
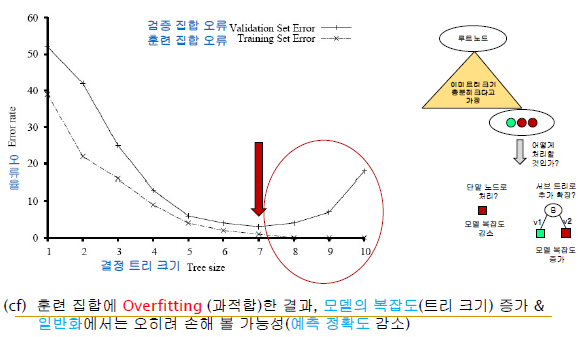
-Traning Set Error는 모델의 복잡도가 증가할수록 에러율이 감소함
-but, Validation Set Error는 학습 데이터를 제외한 나머지 데이터인데 모델의 복잡도가 증가할수록 에러율이 감소하는데 모델의 복잡도가 어느 순간의 복잡도를 넘어가게 되면 에러율이 증가하는 경우가 생길 수 있음
-위의 경우는 학습 데이터에 너무 Overfitting(과적합)한 결과임 -> 학습 데이터가 어느정도 한쪽으로 치우쳐져 있다는 말
-즉, 과도하게 훈련 데이터에 맞춰서 모델 복잡도가 증가하게 되면 일반적인 데이터에 대한 예측 성능이 감소 / 학습 데이터에 100%, 너무 과도하게 맞추면 안됨
■ Loss Function(손실 함수)

-얼마만큼 틀렸냐 하는 정량적인 수치가 포함됨
- Loss function, L(x,y,y^)
-x: 입력값, y: 정답, y^: 예측치
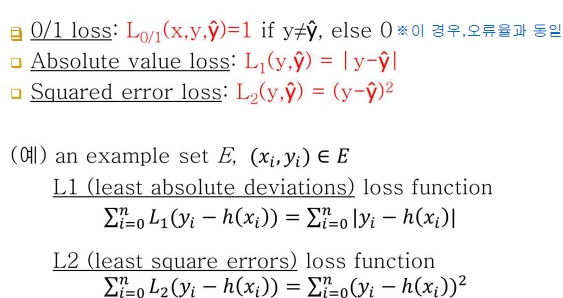
-0/1 loss: 일치하면 0, 틀리면 1
-Absolute value loss: 하나의 테스트 건에 대해서 / 틀렸다고 치더라도 얼마만큼의 차로 틀렸는지가 반영됨(정답과 어느정도의 차로 예측했는지)
-Squared error loss: Absolute value loss 값에 제곱 / 위의 경우처럼 일차식으로 구하면 값이 두드러지게 보이지 않을 때 사용
■ Choosing the Best Hypothesis(최고의 가설 선택)

-L(y,h(x)): example 각각의 {정답(y)과 내가 받아낸 가설함수의 예측치(h(x))}랑 모든 example마다 손실을 다 더한 값이 가장 작은 것이 최고의 가설
-N으로 나누면 평균이 되는데 딱히 의미는 없음
-즉, 정답과 예측치의 차가 가장 작도록 / 가장 정답에 가까울수록 best hypothesis가 된다는 의미
■ Regression Linear Models

-위 예시에서 공통점은 한 입력 데이터의 표현이 일차식으로 조합되어 있음
-휘귀는 조합한 수치값 그 자체를 출력, 분류는 일차식으로 계산된 값을 가지고도 어떠한 경계치를 기준으로 이산화된 라벨을 출력하게 됨
-
Linear regression(선형 회귀)
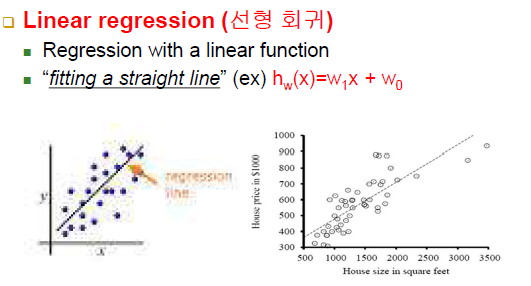
-일차원 입력을 받아 일차원 출력을 냄
-사례들과 오차가 가장 작은 직선(w1, w0)을 찾는 과정
-회귀 문제인 경우 직선만 찾으면 바로 사용할 수 있음 -
Linear Classification(선형 분류)
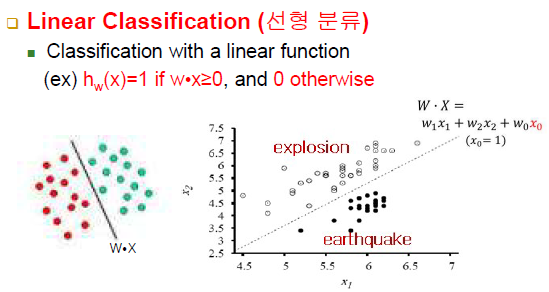
-explosion 점들과 earthquake 점들은 각각 출력 라벨(클래스 라벨)로 생각
-직선보다 위쪽이냐 아래쪽이냐가 중요 / 직선은 클래스를 둘 중에서 어느쪽으로 판별할 지에 대한 결정 경계가 됨 -
Univariate Linear Regression(일변수 선형 회귀)
-최적의 직선 찾기: 각각의 사례의 오차(loss)의 합(손실 함수)이 최소가 되는 직선을 찾아야 함
-xj: 입력값 yj: 그에 따른 정답 출력
-시그마 부분: 모든 사례의 (예측치 - 정답 출력)^2(오차)의 합 -> 쉽게 말해 오차의 합, loss function의 minimize / 이 식에서 모르는 것은 w1와 w0뿐임, 다시 말해 이 식은 w1과 w0에 대한 식으로 생각할 수 있음 / w1,w0가 독립변수 , 그에 따른 loss가 종속 변수
-loss가 가장 작을 때의 w1,w0를 찾는 것

-w* = arg minw Loss(hw)만 찾으면 됨
- Gradient Descent(기울기 하강) on Weight Space

-기울기가 내려가는 방향으로 weight를 변경
-좌측 하단 식은 각각 wo,w1에 대해 편미분 했을 때의 값 즉, 도출된 값은 기울기
-우측 하단 식은 w0,w1의 더 나은 쪽으로의 업데이트 과정 / 파란색 박스의 계산에 따라 증가되거나 감소되거나 하는 변화를 줘서 새롭게 weight를 업데이트(가중치를 새롭게 고침)
-계수 2는 알파에 흡수됨 / - 부호는 기울기가 내려가는 방향으로 하기 위해 부호 변환 / 알파는 사용자가 별도의 파라미터 값으로 부여
-학습 공식(가중치 공식): 초기 w0,w1 값을 랜덤하게 부여하고 (y - hw(x)) 부분을 더하거나 빼거나 하는 과정을 통해 w0,w1 즉, 파라미터 값을 변화시키면서 손실의 합을 줄여나가는 과정
-(y - hw(x)) > 0: 정답에 예측치가 모자람
-(y - hw(x)) < 0: 정답보다 과한 예측

-
Batch(일괄적) gradient descent learning rule
-학습 데이터 각각의 오차가 다 모일 때까지 weight update가 일어나지 않음, 모든 학습 데이터의 오차가 다 계산된 후 모여야 w가 갱신됨
-직전에 바뀐 w0, w1에 대한 것 즉, 변경된 값을 사용하기 때문에 ex) 10개의 데이터의 오차의 합을 고려해 고치지만 그 과정 자체를 여러 번 반복하게 됨
-학습 데이터가 많을수록 batch 처리를 사용하게 되면 매우 느림 -
Stochastic(확률적) gradient descent learning rule
-학습 데이터 한 개에 맞춰서 직선 함수를 고치는 식
-변경이 빨라지게 때문에 속도는 빠름 -
Linear Classification(선형 분류) with a Hard Threshold

-직선을 구하지만 regression을 적용하는 것이 아님
-선형 결정 경계 vs 비선형 결정 경계
ex) Earthquake and Nuclear Explosion Data
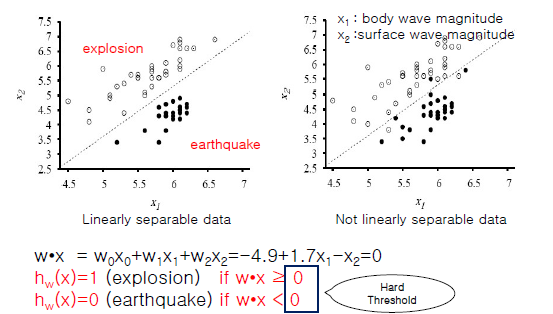
-직선을 알고있다는 가정, 새로운 좌표가 입력으로 들어왔을 때
wx = -4.9 + 1.7x1 - x2 = 0 이 식에 대입했을 때 양수면 그 직선보다 위쪽(폭발), 음수면 직선보다 아래(지진)임을 알 수 있음
-즉, 직선은 경계 역할만 하게 됨 / class 라벨링

-threshold(임계값) function
-분류던 회귀던 일차 직선(지식) 구하는 식은 똑같음
-Hard Threshold: 임계값이 0, 1처럼 극단적
-
Training Error Curve(in Case of Usiing Hard Threshold)
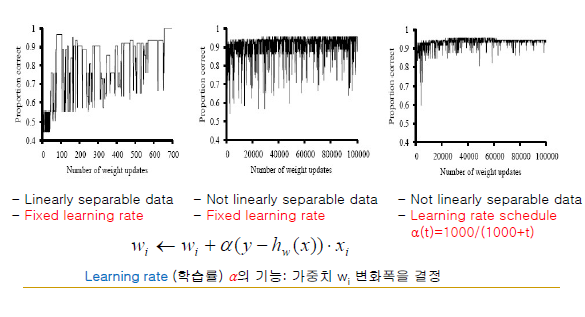
-x축: weight 갱신 주기(횟수), y축: 정답률
-Learning rate(학습률) 알파의 기능: 가중치 wi 변화폭(진폭)을 결정
-오른쪽 그림의 laerning rate 알파는 변화폭이 점점 줄어듦, 전반적으로 깔끔한 수렴을 보임
-최적점을 찾는데 처음에는 큰 폭으로 찾다가 점점 미세 조정에 들어감 -
Linear Classification(선형 분류) with Logistic Regression

-hard threshold는 임계치를 0 또는 1로 극단적으로 나눔
-<hard threshold의 문제점>
-미분불가능
-불연속함수
-예측하기 어려움
-0 or 1이라는 극단적인 예측치
-<Logistic function(=Sigmoid function)>
-연속함수, 미분가능
-함수식: e의 지수항 자체가 양수라 전체 값이 항상 1보다 작거나 같음, hard threshold와 다른 점은 0과 1사이의 어떤 값도 나올 수 있음 -
Logistic Function(=Sigmoid Function)
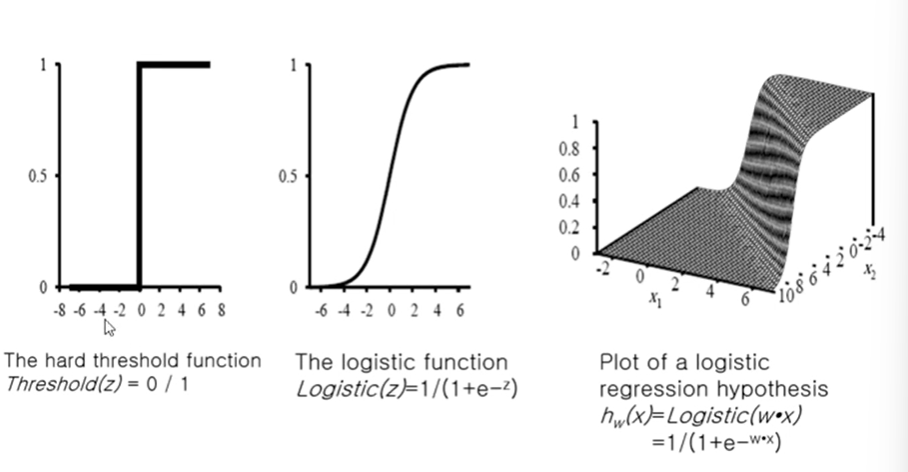
-x축은 weight * 일차식의 수치값
-y축은 threshold의 출력값
-hard threshold - 불연속함수, 값이 0 or 1만 존재
-logistic function - x축 0을 중심으로 y축 값이 연속적인 값을 가짐, 변화를 급격하게 가지지 않음, 수렴하는데에도 도움을 줌, soft threshold라고도 부름 -
Linear Classification(선형 분류) with Logistic Regression
-Weight update rule<Chain learning rule(체인 학습 규칙)>

-hw(x)(1-hw(x))가 추가됨 -
Training Error Curve
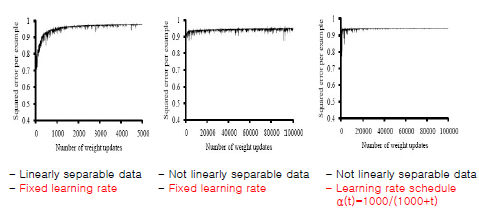
-hard threshold가 아닌 Logistic Function(soft threshold)로 변경했을 때
-같은 데이터임에도 불구하고 잘 수렴하는 것을 보임

