■ Nonparametric Models(비-모수 모델)
- parametric Model(모수 모델)
- 결정트리, 직선(일차식), 신경망 등등
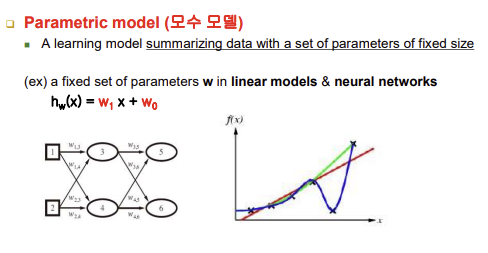
- 인간이 일반화된 함수식 모양을 줌 -> 이후 인공지능이 파라미터만 알아내면 가설함수 즉, 학습 결과물을 얻을 수 있는 모델들: 모수 모델 / 이때 파라미터 값을 구체적으로 알아내는 과정이 learning임
- 신경망에서 여러 개의 뉴런이 있을 때는 파라미터 개수가 늘어나는 것이지 전체적으로 하나의 큰 함수라고 볼 수 있음
- 신경망에서는 다수의 weight의 가중치들을 알아내기 위해 학습을 진행함, 주어진 학습 데이터에 맞도록 역전파 알고리즘을 사용해서 weight값을 갱신(업데이트)함 즉, 파라미터의 가장 최적화된 값을 찾아내는 과정
- f(x): 학습의 목적 함수(target function), x: 입력 / 점들은 사례들을 모아놓은 것임 / 학습: f(x)를 대신할 수 있는 가설 함수(h(x))를 찾는 과정
- h(x)를 통해 모든 입력에 대한 출력을 줄 수 있음(점 6개의 사례로 가설함수를 얻고 그 이외의 가능한 모든 입력들에 대해서 출력을 낼 줄 아는 함수를 얻어서 쓴다는 의미) 그러므로 h(x)는 f(x)와 100% 동일할 수 없음
- 모수 모델의 학습 특징: 주어진 학습 데이터와 일치하되 입력 가능한 모든 입력에 대해서 아주 일반화(범용적)된 지식을 학습과정 동안에 얻으려고 하는 노력, 비-모수 모델에 비해서 모수 모델은 학습 시간이 매우 오래 걸림 but 이점은 구체적인 함수가 구해지고나면 모든 입력(전 범위)에 대해서 출력을 낼 수 있다는 점이 있음
■ Nonparametric Models(비-모수 모델)

- 애써서 학습 단계에서 주어진 학습 데이터에 다 일치하면서 모든 입력에 적용가능한 일반화된 가설함수를 얻는 노력 x
- 학습 데이터 그 자체를 테스트 타임(적용 단계) 때 학습 데이터를 이용
- 극단적으로 학습 과정이 없다고 볼 수 있음
- 모수 모델: 적용하기 이전에 일반화된 함수를 얻는 것을 먼저 하고 그 결과물을 적용(테스트)하는 것 -> offline learning
- 비-모수 모델: 실제 학습한 걸 적용하는 것과 학습하는 것이 어우러져서 돌아가는 것 -> online learning, 테스트 시 바쁨
- 현재 입력에 맞춰서 제일 가까운 학습 데이터를 모음(모수 모델과 다르게 주어진 모든 데이터를 다 사용할 필요가 없음)
- 비-모수 모델 = instance-based learning(개체-기반 학습): 개별 사례들을 가지고 그 사례들을 직접 이용해서 현재 문제에 대한 해법을 찾는 것
- k-nearest neighber models(새로운 입력에 제일 가까운 학습 데이터 k개): k-NN classification(k-NN 분류, class label), k-NN regression(k-NN 회귀, 수치)
■ Parametric Linear Classification(모수 선형 분류)
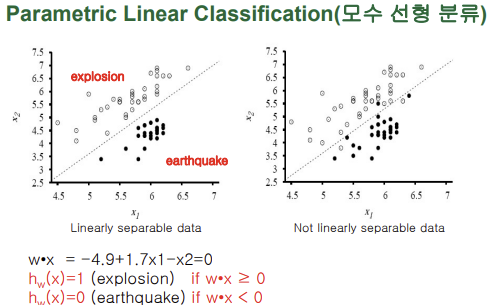
-새로운 입력에 대해 explosion이냐 earthquake냐를 판단하기 위해 사전에 미리 학습단계에서 주어진 사례(학습 데이터)를 가지고 결정 경계(일차 함수)를 미리 찾아냄 -> 이 함수는 어떤 점이든간에 출력을 판별할 수 있는 굉장히 일반화된 함수임
-테스트는 빠르고 이 일반적인 함수를 찾아내는 게 오래걸림
-함수를 찾은 순간 인스턴스인 학습 데이터는 더 이상 필요 없음
■ k-Nearest-Neighbors (k-NN) Classification
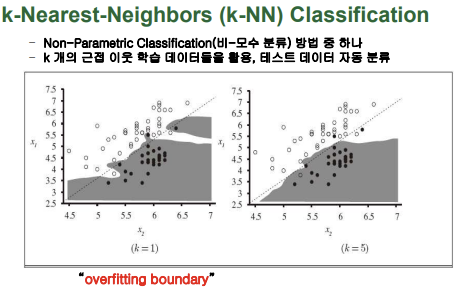
- k개의 근접 이웃 학습 데이터들을 활용
- 경계를 나타내는 함수를 미리 얻어놓는 것이 아님
- ex) k가 1일 때 입력 데이터와 가장 가까운 학습 데이터를 찾아 그 데이터의 출력을 활용해 입력 데이터의 출력을 판별
- k가 짝수이면 좀 곤란한 경우가 생길 수 있음(반대되는 경우의 수가 동일할 때)
- k값이 줄어들수록 데이터에 따라 굉장이 예민하고 복잡하게 나타나고 k값이 증가할수록 부드러운 모양을 띔 but, 너무 커서도 안됨 즉, k값을 적절히 설정해줘야 함
- overffiting: 학습 데이터에 과도하게 맞추는 것, 너무 민감하게 복잡한 결정 경계를 찾는 것은 좋지 않음
- 입력 데이터에 대해 존재하는 모든 학습 데이터와의 거리계산이 수행되어야 함, 학습 데이터가 많을수록 and 입력 차원이 커질수록 계산량이 훨씬 많아지게 됨
- 모수 모델: 학습 단계에서 고생을 많이 하고 적용 단계에서는 굉장히 빠름(바로바로 출력을 얻을 수 있음), 실시간성이 필요한 경우에 적합함
- 비-모수 모델: 학습 단계는 없다고 볼 수 있음, 적용 단계에서 시간이 오래걸림(거리 계산), 실시간성이 필요한 경우에 부적합함
■ Parametric Linear Regression(모수 선형 회귀)
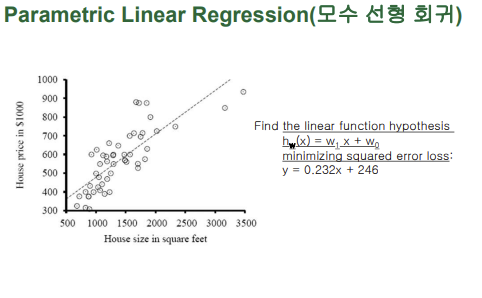
-새로운 입력에 대해 수칫값(출력)을 알아내기 위한 과정
■ Nonparametric Regression(비-모수 회귀)
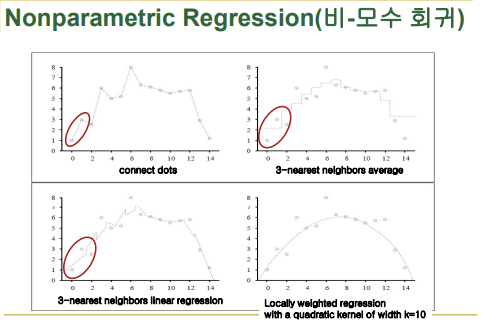
-4 가지 경우 학습 데이터는 동일
-새로운 입력에 대해 출력을 어떻게 계산하는지에 대한 방법
-연결된 점선이 함수를 의미하는 것이 아님
-connect dots: 새로운 입력에 대해 가장 가까운 두 점(입력 데이터보다 가장 가까운 작은점, 가장 가까운 큰점)을 찾아 두 점을 잇는 직선 함수를 찾는 것, 이 직선 함수는 새로운 입력에 대해 적용 단계에서 구하는 것임
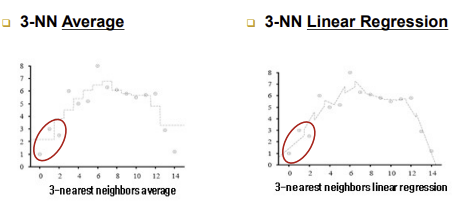
- 3-nearest neighbor(3-NN) average:
-새로운 입력에 대해 가장 가까운 3 개의 학습 데이터를 구함 -> 3 개 데이터 높이의 평균을 구함
-참고하는 이웃이 바뀌지 않으면 내 값은 고정되어 있음(계단형)- 3-nearest neighbors(3-NN) linear regression:
-직선이 세 개의 점과의 출력 차의 합(손실함수, 오차값)이 최소가 되는 함수 찾기(평균으로 구하는 것이 아님)- Locally weighted regression:
-새로 주어진 입력에 지역적으로 얼마나 더 가까우냐에 따라 가중치가 적용된 회귀■ Locally Weighted Regression(지역 가중 회귀)
- idea
-입력에 대해 가까운 출력일수록 weight(가중치)를 크게 줌
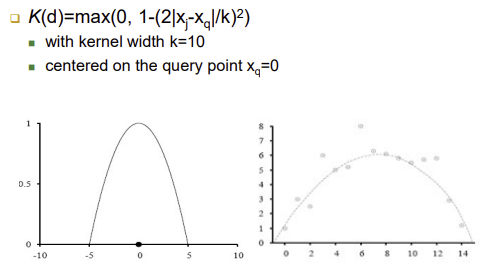
-거리에 반비례 하게 weight를 줌- Kernel function(커널함수), K(Distance(Xj,Xq))
-거리에 반비례한 함수, 여러 가지 가능
-(Xj-Xq): 이 값이 0이라는 건 거리차가 0이라는 의미이므로 weight를 100% 반영한다는 뜻, 하지만 위의 값에 차이가 생길수록 weight의 값이 작아지게 됨
-k값에 따라 그래프의 모양이 달라짐 - 완만한 곡선이거나 가파르거나
-지역 가중 회귀 전의 3 가지 경우들은 간단하게 말해 다수결을 따르는 것이고, 지역 가중 회귀는 각자가 값을 가지고 있어 따로 수치 계산을 필요로 하는 것- ex: Quadratic Kernel
-K(d)=max(0,1(2|x|/k)^2) // d: distance