Reinforcement Learning(AI-21)

■ Reinforcement Learning(RL)

-환경에 에이전트가 놓여서 상호작용함(에이전트의 행동으로 환경 변화를 유발시키고 변화되는 환경상태를 에이전트가 다시 인식해서 반복)
-환경이 에이전트에게 피드백을 reward(보상값)형태로 주게 됨
-ex) s0상태에서 a0의 액션을 했을 때 r0의 reward를 받아 s1상태가 됨
-reward의 합이 최대가 될 수 있는 바람직한 행동을 선택 - 행동 선택 방식
-Γ(감마, discount factor): 시간이 지나서 얻어지는 reward의 값을 감소시켜서 더하도록 하는 역할/ why? - 현재 당장 얻어질 reward가 내 행동 결정에 영향을 더 많이 미쳐야하기 때문임
-학습 목표: reward의 합이 최대가 될 수 있는 action policy를 배우는 것

■ Markov Decision Process(MDP)

-에이전트가 강화학습 상황에서 어떻게 해야 보상의 합이 커지는지 고민
-supervised learning과의 차이점: 상태가 계속 바뀜에 따라 새로운 상태에 맞는 행동을 끊임 없이 해야 함 -> 이때 어떤 행동을 해야 환경이 주는 reward의 합이 가장 클 지 고민하면서 행동하는 것, 학습자의 재량권이 어느 정도 있다고 볼 수 있음(능동적 행동 결정)

• MDP tuple <S, A, P, R, Γ>
  -S: search space(탐색 공간), 가능한 상태들의 집합
  -A: 에이전트가 취할 수 있는 행동들의 종류(action들의 집합)
  -P: 상태 전이 확률 분포(행렬), P(s,a,s'): s-기존상태, a-action, s'-다음상태 즉, s상태에서 a행동을 했을 때 s'으로 갈 확률
  -R: 보상 함수, R(s,a): s상태에서 a행동을 했을 때 보상치를 결정하는 함수
  -Γ: discount factor: 미래에 주어질 reward의 비중을 낮추기 위함

• A (stochastic - 확률적) policy π: 확률적 표현으로 policy를 얻는 것(각 행동마다의 확률을 통해 행동 결정, 좀 더 어려움)

• A (Deterministic - 결정적) policy π: 각 상태 당 하나의 행동 쌍으로 표현되는 경우(행동이 하나로 고정됨)

• An optimal(최적의) policy π*: 환경으로 부터 받게되는 reward의 합이 가장 큰 것을 보장하는 policy

■ Value Functions (가치 함수들)

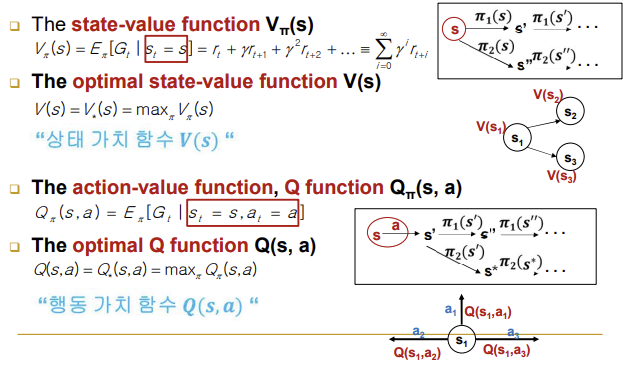
• The state-value function Vπ(s): s에서부터 π(policy)에 따라서 행동을 결정, 바뀐 상태에서도 π에 따라서 행동을 해나감 / π에 따라서 끝까지 간다고 했을 때 얻어지는 모든 reward들의 합 즉, 각 상태마다 얻게되는 reward들의 합이 다를 것이기 때문에 이는 상태에 대한 가치를 나타냄

• The optimal state-value function V(s): 모든 policy를 적용했을 때 얻을 수 있는 reward의 합 중 가장 큰 것

• The action-value function, Q function Qπ(s,a): 어떤 상태에서 어떤 행동을 했을 때의 가치를 판단하는 함수 / 같은 행동이라도 어떤 상태에서 행동하냐에 따라 reward 값이 달라지기 때문에 인자에 s도 포함되어야 함

• The optimal Q function Q(s,a): 가능한 policy 전체에 대해 가장 큰 Q값을 얻어주는 fuction(value 값을 가장 크게 해주는 놈)

• Vπ(s)와 Qπ(s,a)의 차이점: action이 명시되지 않은 것은 s부터 시작해서 policy π에 의해 action이 결정됨, action이 명시된 것은 현재 상태에서는 a 행동을 하고 그 이후부터는 policy π를 따라감

■ Bellman Equation

• Q(s,a): 현재 상태에서의 reward + {s에서 s'으로 갈 확률 * s'부터 시작해서 얻어지는 reward들의 합(V(s'))}들의 합 -> discount factor를 적용

■ Q Learning(Q 학습, 가치 함수)

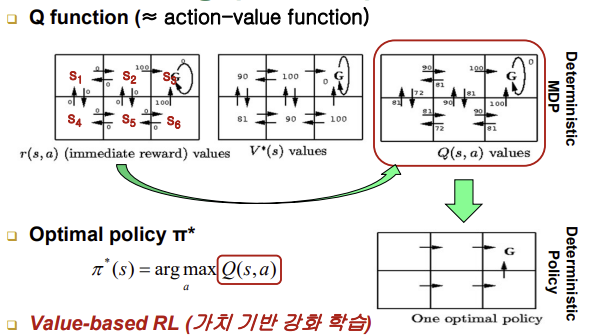
• optimal Q function을 배우는 것, policy를 배워야지 왜 Q function을 배우느냐 -> optimal한 Q function은 사실 optimal한 policy를 의미하기도 함
• π*(s)(s에서 최적의 행동을 결정하는 policy) = arg max Q(s,a)(s에서 Q값이 최대가 될 수 있는 행동)

  Q Learning은 근본적으로 최적의 평가할 수 있는 어떤 상태에서 어떤 행동을 하는 것이 얼마나 바람직한 것인지에 대한 판단을 한 번에 알 수 없고 이거를 점진적으로 학습하는 동안에 배움, 가치 함수를 배움, 경험을 많이 할수록 가치평가가 더 정확하게 나옴, 가치 함수가 더 이상 좋아질 수 없도록 판단 능력이 최적화 되었다는 말은 Q가 다 얻어졌다는 말임 -> 어떤 상태이던간에 최적의 행동은 저절로 결정됨 / 최적의 policy를 얻는 방향으로 학습하는 것이 아니라 가치 함수를 배우려고 하는 것임(최적의 Q), 매번 Q 값이 큰 행동을 하면 됨 ==> Value-based RL

■ Learning Q Function

• 왼쪽 그림은 R에서 오른쪽으로 가는 현재까지의 Q값이 72임
• Traning rlue에 의해서 업데이트 됨
• Γ(discount factor)=0.9, R2에서 할 수 있는 행동들의 Q값 중 max를 골라 곱하게 됨, 이 값과 현재 상태의 reward값을 더했더니 90이라는 값이 나오고 이 값이 Q값에 새롭게 업데이트 되게 됨
• 이후 또 다음 상태에 대한 과정을 진행할 때는 Γ가 아닌 Γ^2을 대입해주어야 함(비중을 점차 줄여나가겠다는 의미)
• 최적의 Q값에 도달하면 학습 종료(수렴할 때까지, 헥터가 없는 Q(s,a))

■ Q Tables

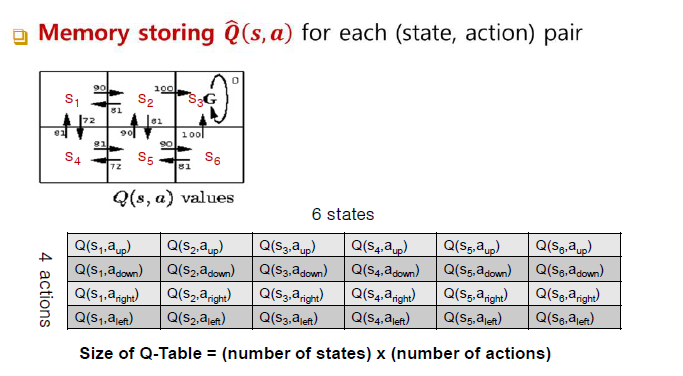
• Q-Table 사이즈는 state 개수 x action 수
• 처음에는 모든 Q값을 0으로 채워놓고 시작
• 초기상태를 정하고 거기서부터 Q값이 채워지고 나머지 table들도 계속해서 업데이트 되게 됨, 이후 값의 변경이 없이 수렴하게 되면 학습 종료

■ Q learning Algorithm

-필드 값 전부 0으로 설정
-초기 상태 선택
-행동 선택(어떻게 선택할 지가 중요)
-즉각적인 reward r 수령, 새로운 상태로 건너감
-그림에서처럼 Q(s2,adown) 값이 업데이트 되고 s'인 s5가 s 즉, 현재상태가 되어 이 과정을 가시 반복하게 됨

■ Exploitation vs Exploration

• Action Selection Strategies
• Only ecploitation
  -Q헥터(s,a)가 최대인 action a를 선택
  -위 사진의 예시처럼 s2, s5 둘의 Q값만 업데이트 되는 불상사가 생길 수 있음
  -즉, 새로운 다른 action을 모험적으로 시도하지 않게 됨
  -Q 수렴 조건을 만족하기 어려움
  -Q값이 제일 높은 한 놈에만 필연적으로 선택하게 함
• Allowing exploration
  -확률 기반 선택 방법: 전체 행동들이 본인 Q값에 따라서 그 행동이 선택될 가능성을 나누어 가짐(분모: 모든 행동들에 대한 Q값의 합, 분자: 특정 행동에 대한 Q값)
  -ε 임의 선택 방법: 확률 ε만큼 random selection, 확률 (1-ε)만큼 Q헥터(s,a)가 최대인 행동 선택 / ε값이 중요

■ Convergence of Q Learning

• Convergence condition(수렴 조건)
  -MDP
  -reward 값이 dounded된 경계여야 함
  -모든 가능한 state-action 쌍(s,a)를 무한대로 종종 방문해야 함 -> 상태 or 행동의 수가 너무 많아지게 되면 table size가 커지게 되고 그 커진 만큼 각 쌍들을 무한히 방문하며 동작해야 하기 때문에 학습 시간이 굉장히 오래걸리게 됨

■ Value Function Approximatation(가치 함수 근사)

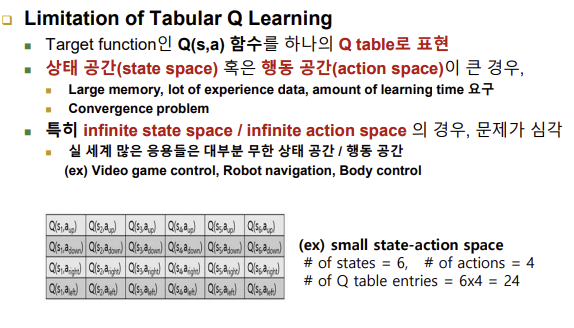
• Mimitation of Tabular Q Learning
  -상태 공간 혹은 행동 공간이 큰 경우: 큰 메모리, 많은 경험 데이터, 많은 학습 시간을 요구
• infinite state space / infinite action space
  -실 세계 많은 응용들은 대부분 무한 상태/행동 공간
• 대안

  
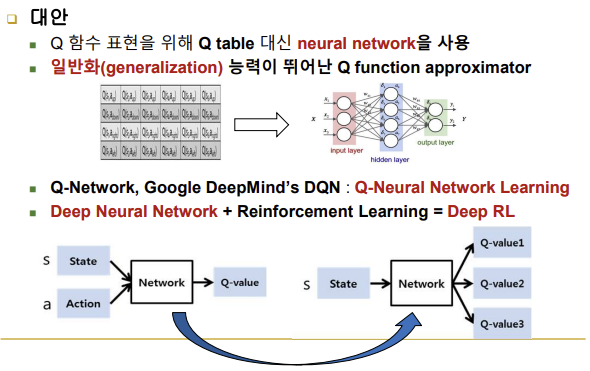
  -Q table 대신 neural network 사용
  -일반화 능력이 뛰어난 Q function approximator
  -강화학습의 학습 데이터는 사람이 주는 게 아니라 자신이 경험해야만 생김
  -결론적으로 끊임없이 새로운 경험 데이터로 neural network를 고칠 뿐만 아니라 현재까지 학습해놓은 NN의 도움을 받아 다른 상태와 다른 행동의 Q값도 예측해서 이용할 수 있음
  -Deep Neural Network(적은 경험 데이터를 가지고 일반화시켜서 경험하지 않은 것에 대해 예측할 수 있도록 하는 것, 감독학습) + Reinforcement Learning(강화 학습) = Deep RL
  -요즘의 심층 강화 학습은 입력을 상태, 행동 둘 다 주는 게 아니라 상태만 줌, 행동의 개수는 가능한 적게, 행동 개수만큼 출력 개수가 나오도록 설계

■ DQN의 2 가지 주요 기술

■ Experience Replay Buffer (경험 재현 버퍼)

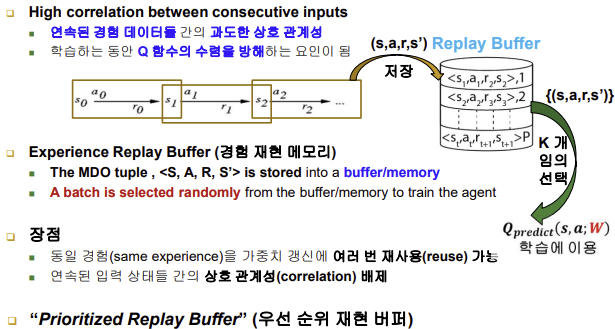
• 이 버퍼는 에이전트가 경험한 데이터를 저장하고 나중에 재사용할 수 있는 메모리 구조임, K개를 임의로 선택해서 학습에 이용
• 장점
  -동일 경험을 가중치 갱신에 여러 번 사용 가능
  -연속된 입력 상태들 간의 상호 관계성 배제

■ Fixed Q Target (고정된 Q 목표 함수)

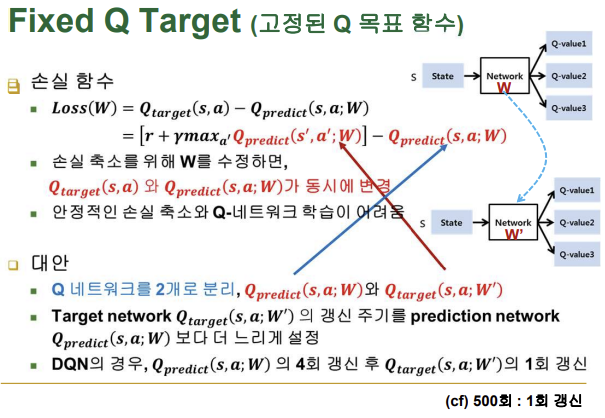
• 손실 함수에서 손실 축소를 위해 W를 수정하면, 타겟 Q값과 예측 Q값이 동시에 변경됨, 이는 안정적인 손실 축소와 Q-네트워크 학습에 어려움을 줌
• 대안
  -Q 네트워크를 각각 타겟 Q, 예측 Q 두 개로 분리
  -타겟 네트워크 Q의 갱신 주기를 예측 네트워크 Q보다 더 느리게 설정
  -이를 통해, DQN 알고리즘의 안정성과 수렴 속도를 향상시킬 수 있음

■ Policy Gradient RL(정책 기울기 강화학습)

• Policy-based RL
  -가치 함수 Q가 아닌 Policy-based, policy를 직접 학습 대상으로 삼음
  -신경망은 일반화 성질이 짙음
  -큰 상태/행동 공간 문제에 적용 가능(DQN에서는 어려울 때)
  -supervised learning에서는 loss함수를 줄이기 위한 식으로 기울기 하강 공식을 만들고 계속 적용
  -policy-based RL은 정답이 없기 때문에 loss가 아니라 reward의 합이 즉, return이 커질 수 있도록, 세타를 미분해서 기울기를 구하고 그 기울기가 상승하는 방향이 되도록 세타를 고치는 갱신 공식을 만들고 계속 적용
  -DQN은 상태가 너무 크지 않고, 행동의 개수도 적은 경우에 쓰기 때문에 경험 데이터가 많지 않아도 학습을 잘 함 즉, 데이터 효율성이 높은 반면 / Policy-based RL은 데이터 효율성이 낮음