■ Problem-Solving Agents

(cf) Planning Agents, Search for Automated Planning
-seq : 앞으로 하고자 하는, 할 거라고 예정되어있는 행동들의 순서(action sequence, plan)
-state: 현재 놓여있는 환경 상태
-goal: 달성해야 하는 목표
-problem: 해결해야 할 문제
-state <- UPDATE-STATE(state,percept): 이때 state는 직전 상태, percept는 sensing된 정보/ 즉 직전 상태에서 percept의 정보를 통해 현재상태로 업데이트(상태추정)
-if seq is empty: 계획이 없으면
-goal <- FORMULATE-PROBLEM(state,goal): 목표 설정
-problem <- FORMULATE-PROBLEM(state,goal): 현재상태에서 목표까지 도달하는 문제
-seq <- SEARCH(problem): 탐색
-FIRST: 맨 앞의 첫번째 행동(지금 당장할 행동)
-REST: 나머지 부분은 저장(다음 순간의 행동, 미래)
■ Problem Formulation & Example Problems
-
ex) Romania Traveling(State Space Search Problem,상태 공간 탐색 문제)
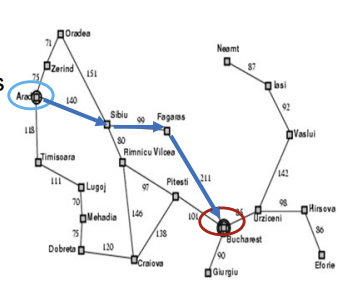
→Formulate the problem(문제 정형화)
-states: being in a certain city
-actions(state transitions,간선, 여기서는 도로망): drive between cities
-initial state: in Arad
-goal condition: be in Bucharest
-[action/path cost]: 행동에 따른 비용, 비용이 최소인 경로가 최적 경로
-solution: [driving] a sequence of cities
※ goal state가 아니라 goal condition이라고 기술하는 경우가 있는 이유: state는 상태 하나, 하지만 이러이러한 조건만 만족하면 돼라고 한다면 어떠한 특정 state가 아니라 특정한 condition만 만족하면 되는 경우가 존재하기 때문 -
ex) Vacuum Cleaner World
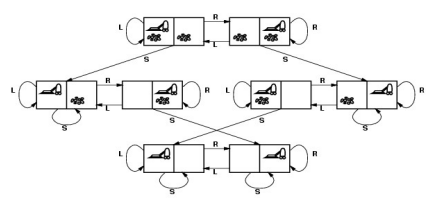
-state(!=percept): 8tates(robot location, clean/dirty_A, clean/dirty_B)
-actions: 간선, 화살표로 표시되어 있음(left, right, suck)
-goal condition: goal state가 아니라 goal condition인 이유는 로봇청소기가 방이 모두 깨끗하다는 가정하에 A방에 있던, B방에 있던 상관 없기 때문임 -
ex) 8-puzzle
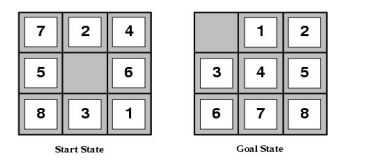
-state: 9!
-actions: move blank left, rught, up ,down(빈칸이 한 가운데에 있을 때만 4가지 동작이 가능)
-initial state, goal condition: the given state
-NP-hard
■ Basic Search Algorithms
-
Tree Search(트리 탐색)
-basic idea: offline, simulated(현실세계x) exploration(탐색) of the state space by generating successors of already-explored states
-목표상태를 찾아가야하는데 어디로 가야할 지 모름 즉, 계속 확장하면서 탐색해야 함
-expanding: 현재 상태가 목표상태가 아닌 것을 알았다면 결국 자식노드를 만들어서 즉, 확장해서 탐색해 나가야 함, 목표상태를 만날 때까지 확장
-Search Strategy(탐색 전략): 어떤 노드부터 확장할 지를 결정
※확장 하다가 목표 상태를 만났음 -> 근데 답은 뭐지??: 목표 state가 답이 아님, 목표 상태에 도달하기 위한 행동들의 sequence가 solution
※ 목표 상태에 도달했는데 solution이 아직 없음 why? 계속 목표 상태를 모르는 상태에서 확장만 했기 때문에 행동들의 sequence가 아직 없다는 것임/ how? 자식 노드 기준에서 부모노드는 하나이므로 부모노드를 찾고 루트노드까지 찾아서 뒤집으면 루트에서 목표까지의 경로 즉, solution이 구해짐
※state는 정보, 이를 자료구조로 표현하면 node -
Search Strategies(탐색 전략/방법)
※Uninfroemed search(무정보 탐색), Informed serach(heuristic)
-strategy는 노드 확장 순서의 정의라고 할 수 있음
→ Search Directions(탐색 방향)
-전향 탐색
-후향 탐색
-양방향 탐색: 서울에서 부산 가려고 함, 경로가 너무 많기 때문에 서울에서 부산가는 경로 탐색과 부산에서 서울가는 경로를 동시에 탐색해서 노드의 수를 줄이는 방법 -
Search Strategy Evaluation(탐색 전략 평가)
-Completeness(완전성): 해가 존재하면 반드시 찾음, goal state가 반드시 하나는 존재, if 만 번 돌려도 한 번이라도 해를 못찾으면 완전성이 없다고 말함 즉, 100%보장
-Optimality(최적성): 최적의 해를 찾을 수 있는 것, 최초로 목표상태를 발견했을 때 최적의 해를 찾는 것을 보장하는 알고리즘, 한 번도 예외없이 최적성을 만족하는 알고리즘이 있는 경우는 거의 없음
-시간, 공간복잡도: 최적의 해를 찾는데 하드웨어의 효율성을 찾는 것임 -
Breadth-First Search(너비 우선 탐색)
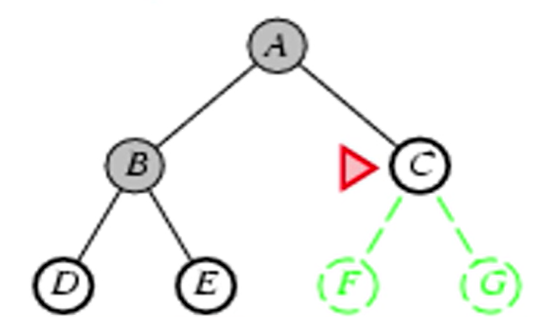
-깊이가 얕은 것부터 탐색해서 확장해나가는 방식
-같은 깊이 레벨의 노드 중에서 어떤 것을 선택해도 상관없음
-fringe: FIFO queue, 다음 탐색 가능한 노드들
-목표상태를 찾고 부모노드를 찾아서 경로를 설정: ex) A-B-E(solution)
-C와 D가 경쟁상대인데 FIFO queue에 의해 먼저 들어간 C가 나오게 됨
→ 특징
-완전성: YES // 모든 노드들을 너비 우선으로 확장해서 탐색하기 때문에 목표 상태는 반드시 찾을 수 밖에 없음, 찾지 못한다는 것은 문제가 잘못된 것
-Time: O(b^d+1) // b: 가짓수, 루트 노드에서 자식노드로 가는 가짓수
-Space: O(b^d+1) // 매순간 만들어지는 것들을 전부 저장하기 때문에
-최적성: YES // cost를 1이라고 생각, 길이가 가장 짧은(step이 가장 짧은) solution을 찾을 수 있느냐: 가능함, 그러므로 최적성을 만족함
※시간과 공간이 깊이의 지수적으로 증가, 기억공간이 가장 큰 문제, 메모리가 너무 많이 필요 -
Uniform Cost Search(최소 비용 우선 탐색),lowest-cost search
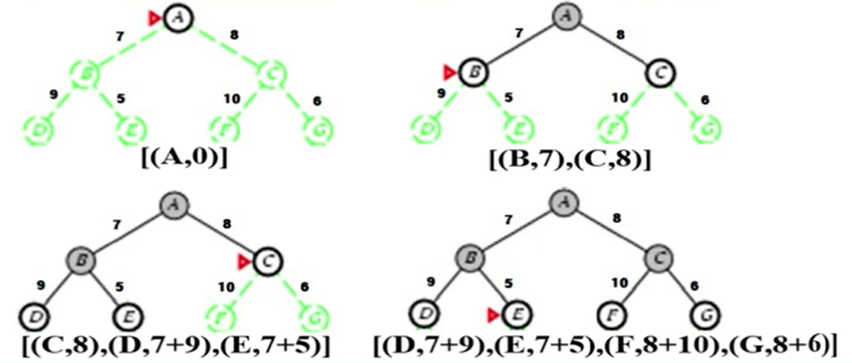
-목표를 찾을 때 비용을 고려, 최소비용을 가지는 노드를 우선적으로 확장
-uniform cost search에 모든 cost가 1인 것이 너비 우선 탐색임
→ 특징
-완전성: YES
-시간, 공간: 지수형태로 커짐
-최적성: YES -
Depth-First Search(깊이 우선 탐색)
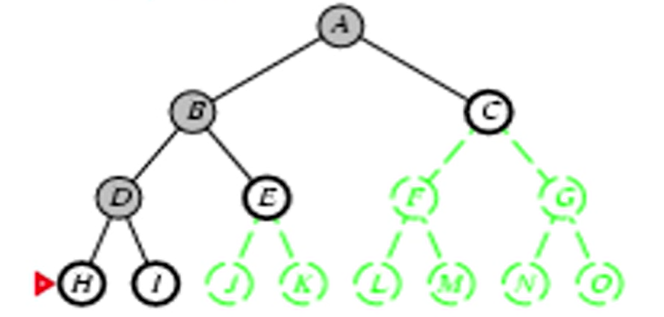
-더 깊은 것을 우선적으로 선택
-fringe: LIFO queue, 사실은 stack
-깊이가 얕은 것을 먼저 선택하면 너비 우선, 깊이가 깊은 것을 먼저 선택하면 깊이 우선
-왼쪽 끝까지 계속 간 후 오르락 내리락 하면서 오른쪽 끝으로 감(백트래킹)
→특징
-완전성: NO // 왼쪽 끝으로 탐색을 계속 진행하는데 왼쪽 탐색 과정에서 loop를 도는 경우에는 해를 찾지 못할수도 있음
-시간: O(b^m) // 목표상태와 상관없이 끝까지 가는 깊이(m), 어쩌면 시간은 너비우선보다 더 오래걸릴수도 있음, terrible if m is much larger than d
-공간: O(bm) // 메모리를 적게 차지함, linear space, 현재노드를 바탕으로 현재노드의 부모들의 메모리에 저장하고 있으면 나머지 노드들을 모두 방문할 수 있음 즉, 깊이에 비례한만큼인 선형 메모리 공간을 필요로 함
-최적성: NO // 목표 상태가 반드시 하나일 거라는 보장이 없음 그림에서 C가 목표상태이고 J가 목표상태 즉, 목표상태가 두 개라고 가정했을 때 더 얕은 C가 아닌 더 깊은 J를 목표 상태로 판단하고 solution을 J까지의 경로로 판단하고 종료하게 되기 때문에 최적성을 만족하지 못할수도 있음
※완전성과 최적성을 만족하지 못한다는 것이 해를 무조건 못찾거나 최적의 해를 찾지 못한다는 의미가 아님 -
Depth-Limited Search(깊이 제한 탐색)

-깊이 우선 탐색에서의 완전성을 보완하기 위한 방법
-그렇다고 완전성과 최적성을 무조건 만족하는 것은 아님
-깊이 제한을 얼마만큼 제한하는지가 까다로운 과정임 -
Iterative Deepening Search(반복적 깊이 탐색)
-무정보 탐색 기법 중에는 효율적임
-깊이 우선 탐색 + 너비 우선 탐색
-깊이 우선 베이스로 시작하고 깊이 제한을 처음에 주고 탐색이 실패하게 되면 깊이 제한을 하나씩 늘려서 다시 시작
→ 특징
-완전성: YES // 깊이 제한이 0부터 전부 탐색을 하기 때문에 완전성을 만족할 수 밖에 없음
-시간: O(b^d) // 너비 우선 탐색에 비해서는 그렇게 오래걸리지는 않음
-공간: O(bd) // 깊이에 비례(깊이 우선 탐색과 동일) 엄청난 장점
-최적성: YES // 깊은 레벨의 goal state보다 얕은 레벨의 goal state를 항상 먼저 찾기 때문에 최적성을 만족하게 됨(step cost가 1일 때) -
Summary of Search Algorithms
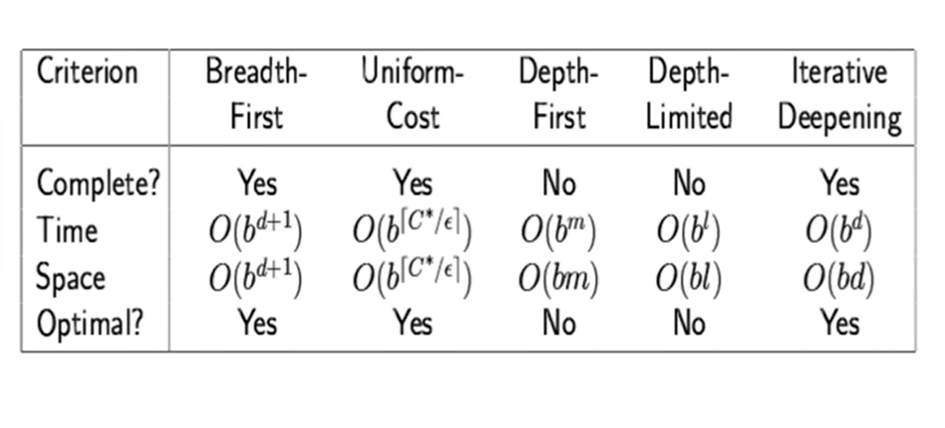
-
Repeated States(반복 상태)

-만약 같은 상태가 다시 반복해서 나오면 같은 상태(노드)를 통합: Graph Search(불필요한 행동을 제한하겠다)

-closed: 저장공간, state들을 담음
-마지막 if문: 확장하려고 선택된 state가 closed 속에 이미 있으면 확장을 하지 않고 closed 속에 없으면 확장을 한다는 의미 / add STATE[node] to closed: 선택한 node가 closed에 없다면 확장을 하는데 그 전에 이 node를 closed에 저장함(원래 확장한 노드는 필요가 없지만 closed에 모아놓음, 확장 후보(fringe)에서는 remove)
-결과적으로 반복적인 불필요한 작업을 하지 않겠다는 의미
