■ Informed Search(= Heuristic Search, 정보를 이용한 탐색)
-목표 노드가 어디있는 지 모르는 상태에서 중요한 것은 어떤 노드들을 먼저 확장해서 탐색할 것인가인데, 이때 informed search는 그 후보들을 평가할 수 있는 평가함수가 존재(f(n) - evaluation function)
■ Best-First Search
-순서하고 상관없이(깊이를 따지지말고) 들어있는 후보들 중에 평가함수가 가장 좋은 것들 찾아서 확장 대상이 되도록 함(Priority Queues)
- Special cases
-Greedy Best-First Search
-A* Search
■ Greedy Best-First Search
-
f(n) = h(n)(heuristic)
-현재 상태 n에서부터 가장 가까운 목표까지의 비용(costs)을 예측한 값
-시작상태가 아닌 현재 상태부터임
-비용은 적을수록 좋음 즉, 그래서 후보들 중에서 h(n)이 가장 좋은 값을 가지는 노드부터 우선적으로 확장을 시도 -
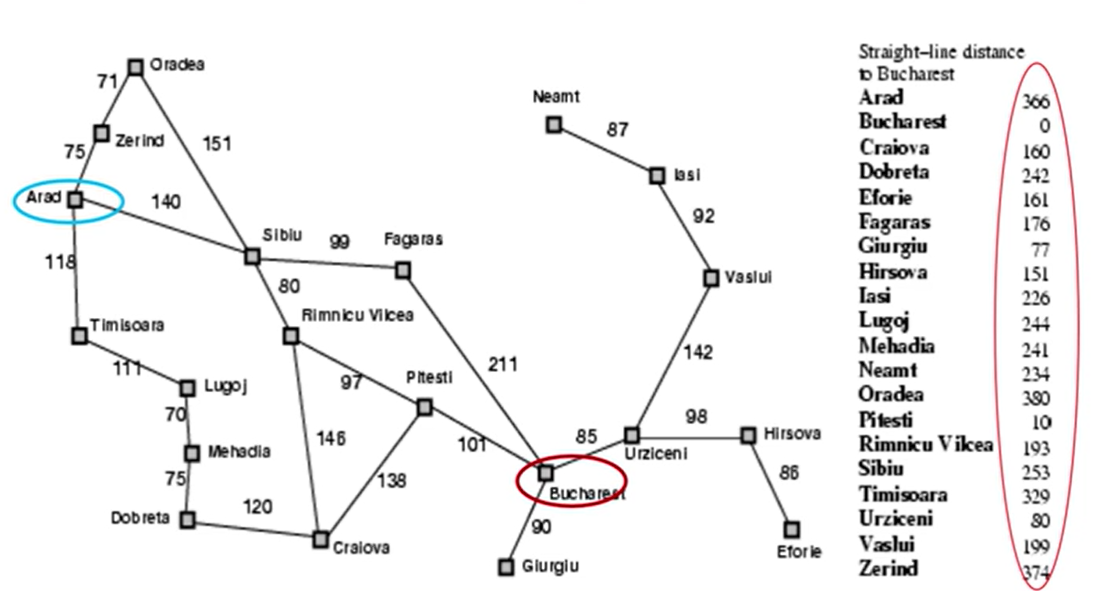
SLD= Straight-Line Distance
-ex) h.sdl(n)= straight-line distance from n to ~~
-목표까지의 경로는 몰라도 현 위치와 목표 위치의 좌표를 대충 안다는 가정하에 직선거리를 구함(여러 장애물들을 일단 무시한 직선거리) -
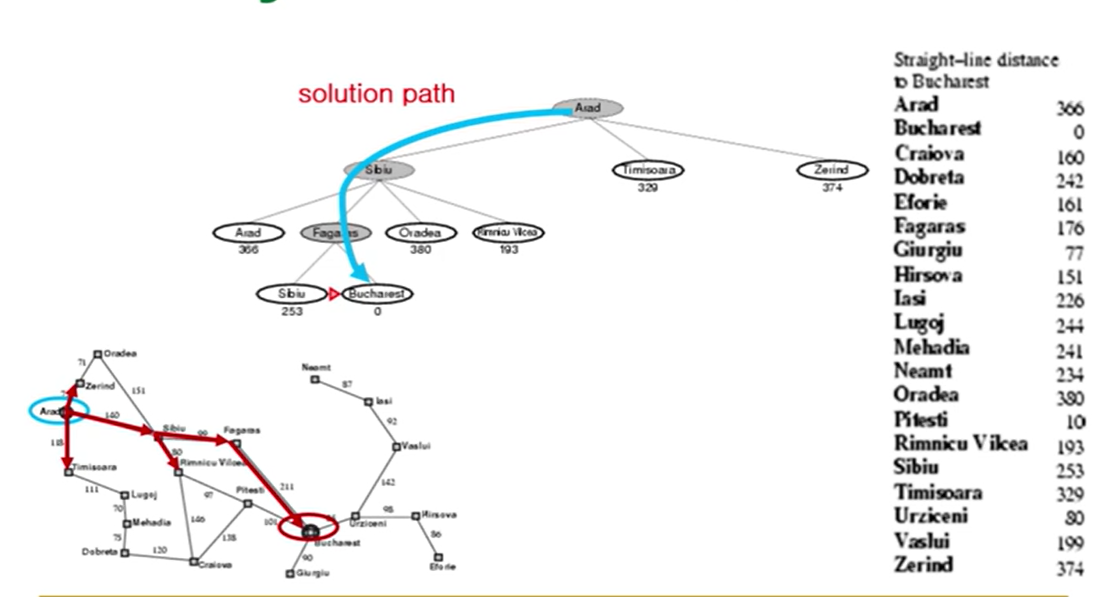
Gbfs
-bfs이긴한데 평가함수를 목표까지 남아 있는 소요 비용 가지고 비용이 작은 것일수록 우선적으로 확장하는 알고리즘
ex) Romania with step costs in km
-여기서 SLD의 값들이 평가함수의 값이 되는 것임
- Properties of Greedy Best-First Search
-time, space: O(b^m)(b는 각 상태 노드에서 next 노드들이 펼쳐질 수 있는 가짓수, 다 다른데 평균치로 b로 생각)(계산량이 너무 많아짐, 너비우선 탐색과 유사 but 너비우선탐색에서는 d를 사용, d는 더 짧은 것 m이 더 길다)(휴리스틱 function이 크게 좌지우지)
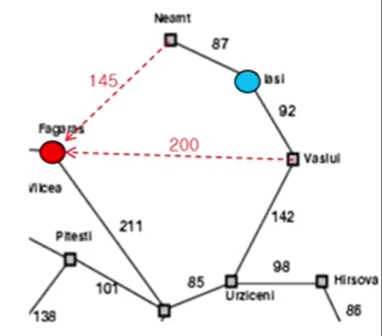
-완전성: solution 한 개는 반드시 찾을 수 있느냐 - No, loop의 경우가 생길 수 있음, 위의 그림에서 예를 들면 파란색 점인 initial node에서 GBRS를 수행하면 평가치가 좋은 위의 경로로 확장을 하게 되는데 이때 확장된 노드에서 목표까지 갈 수 있는 경로가 없기 때문에 결국 initial 노드와 Neant노드를 무한하게 수행하는 구조가 형성됨
-최적성: No- 완전성을 만족하지 못하면 최적성도 만족하지 못함, 완전성을 만족하는 상태에서만이 최적성을 만족하는지에 대한 부분을 따져볼 수 있음
■ A* Search
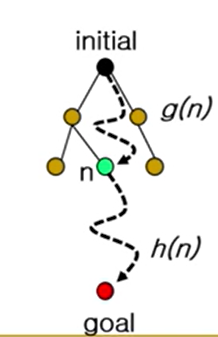
-f(n) = g(n) + h(n)
-g(n): initial node에서 현재 상태 n까지 비용의 평가치
-두 길이가 합쳐져서 평가치가 낮을수록 좋음(비용을 따지고 있기 때문에)
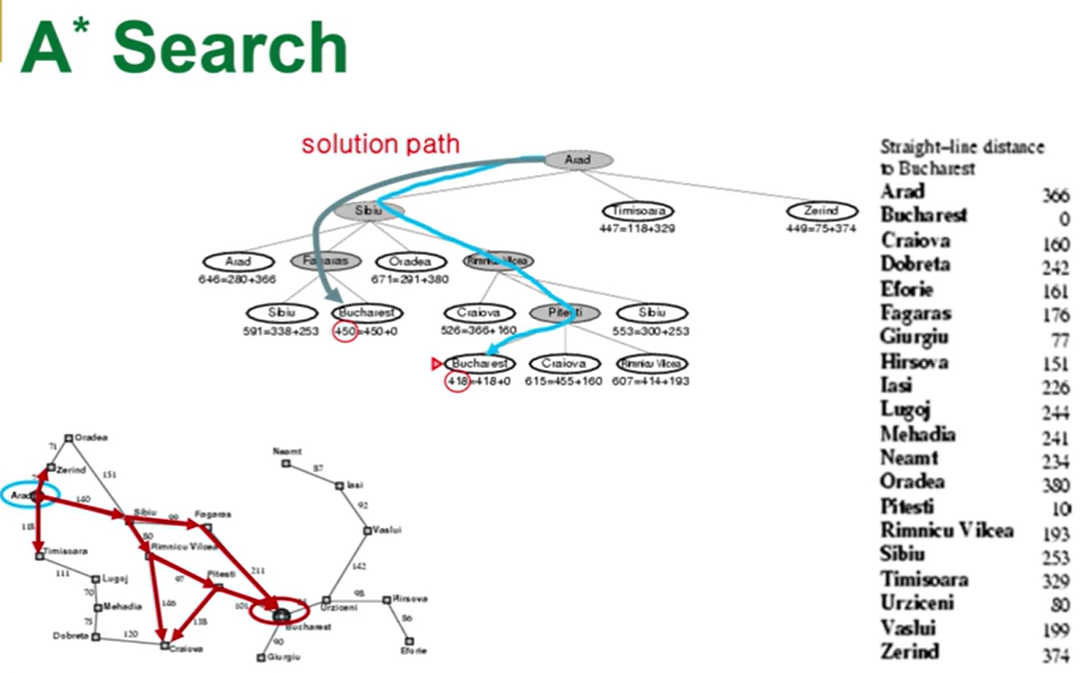
ex)
- 확장 순서: Arad - Sbiu - Rimnicu Vilcea - Fagaras - Pitesti - Bucharest
※주의: Rimnicu Vilcea에서 Pitesti가 아닌 Fagaras를 먼저 확장한다는 점(f(n) 값에 의해서)
- Properties of A* Search
-time, space: O(b^d) - 지수이긴 하지만 빨리 최단경로 해에 도달한다면 시간과 공간에서의 이점이 있을수도 있긴함, 그렇지만 역시 exponential
-완전성: Yes
-최적성: Yes - 경로가 여러 개 있어도 가장 최소비용의 경로를 찾음
■ Admissible Heuristics
-모든 노드 n에 대해서 h(n) <= h*(n) // h(n): 현재 상태에서 목표 상태까지의 실제 cost
-현재 상태에서 목표 상태까지의 cost를 예측할 때 과대 평가를 하지 않는 것(언제나 실제값보다 작게) - 허용성(admissible)
-if h(n) is admissible, a using TREE-SEARCH is optimal(최적성 )
→ex) Straight-Line Distance는 그럼 Admissible Heurisitcs에 속하나? - Yes: 직선거리는 실제거리보다 언제나 작게 예측하기 때문(같은 경우도 존재하긴 하겠지, 실제 거리가 더 짧아질 수는 없다는 말)
→ex) the 8-puzzle:
-h(2): 각 타일별로 목표위치까지 상하좌우 몇 번을 움직여야 하는지(나머지 타일을 다 무시하고 각 타일들이 몇 번 이동해야 목표위치까지 도달할 수 있는지) - total Manhattan distance
-h(1): 각 타일들을 전부 떼어내서 붙이는 것
-둘 다 현실적인 문제의 해답이 아님, 둘 다 Admissible하고 최적 solution을 보장할 수 있긴 함 but 이 문제와 이 최적 solution을 얼마나 효율적으로 찾는지는 다른 문제임(이 문제에 대한 내용이 Dominance)
-h가 낙관적으로 잘못 예측하면 g의 값이 늘어남
■ Dominance
-두 heuristic function이 admissible하다는 가정하에 어떤 것이 더 domoiates(우세)한가에 대한 내용
-if h2(n) >= h1(n) for all n(both admissible) then h2 dominates h1
-h2 is better than h1 for search

-IDS는 무정보탐색 중에서 가장 효율적인 알고리즘
-h 함수가 상한값(실제값)에 가까울수록 즉, 크게 예측할수록 더 우수하다(효율적이다)