✅ 프로그래머스 타겟 넘버
문제링크 : https://programmers.co.kr/learn/courses/30/lessons/43165
숫자를 적절히 더하고 빼서 타겟 넘버를 만드는 방법의 수를 return 하도록 solution 함수를 작성해주세요.
문제 풀이 방법
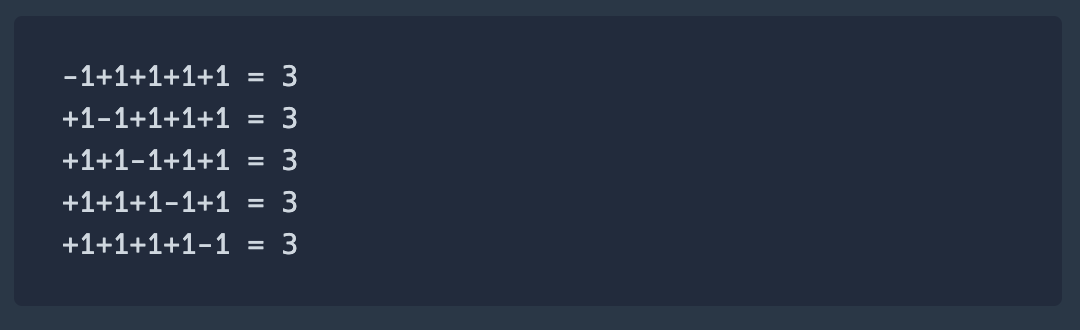
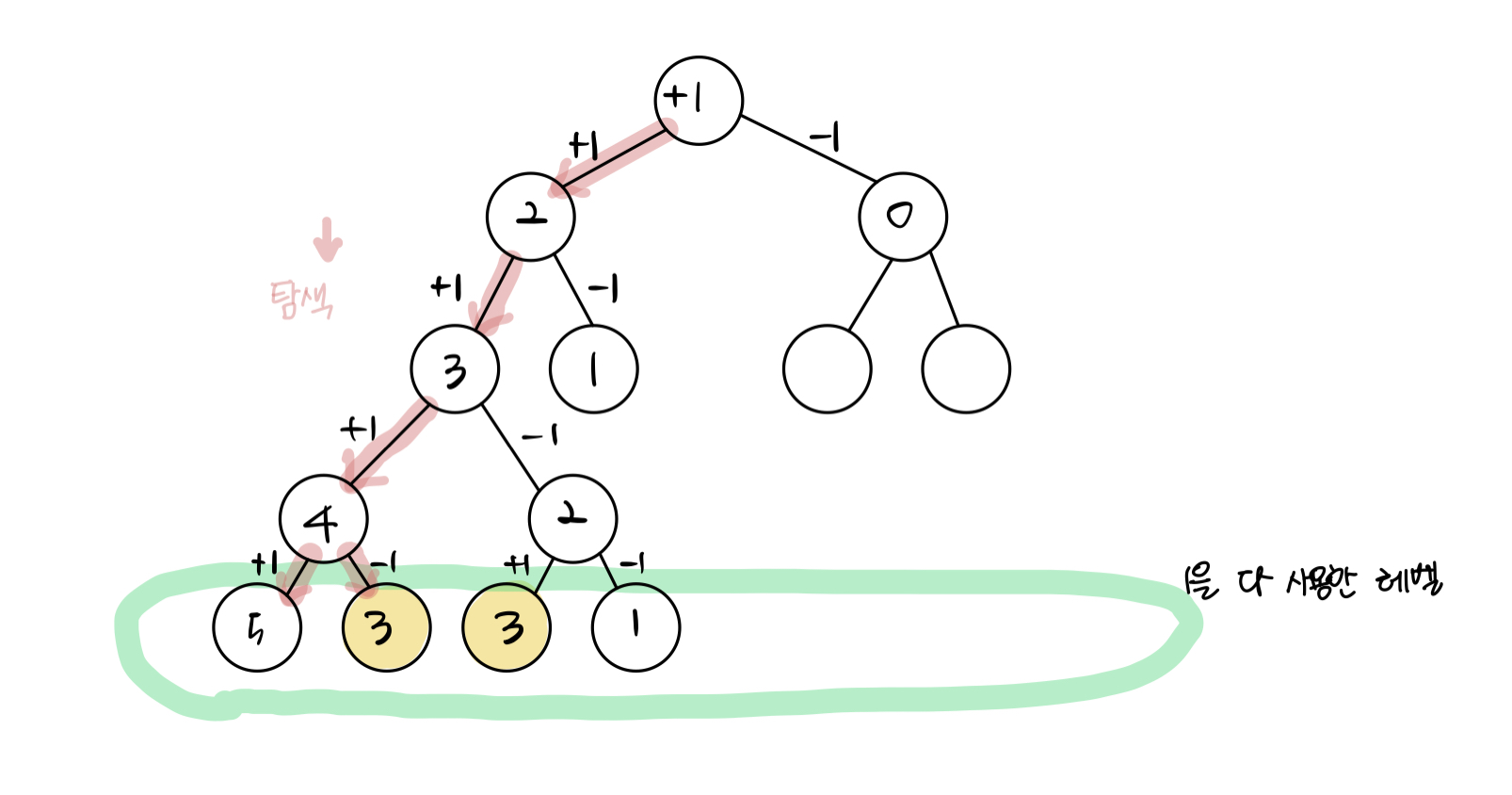
[1,1,1,1,1]로 더하기 또는 빼기를 반복하여 타겟넘버인 3을 만들 수 있는 방법의 수는 위와같이 5가지이다.
주어진 수가 [a,b,c,d,e]가 있다고 하면
이 수들로 더하기 또는 빼기를 반복하여 만들 수 있는 경우의 수는
각각 수별로 +또는 -를 하는 방법 2가지이므로 2의 5승(=32)가지이다.
a부터 e까지 +또는 -연산을 해가며 타겟넘버가 되는지 판단하면 된다.
여기서, 지금까지 연산한 결과에 +또는 -연산한 결과를 또 연산해가며 탐색하므로 재귀방식을 생각해 볼 수 있다.
접근방식
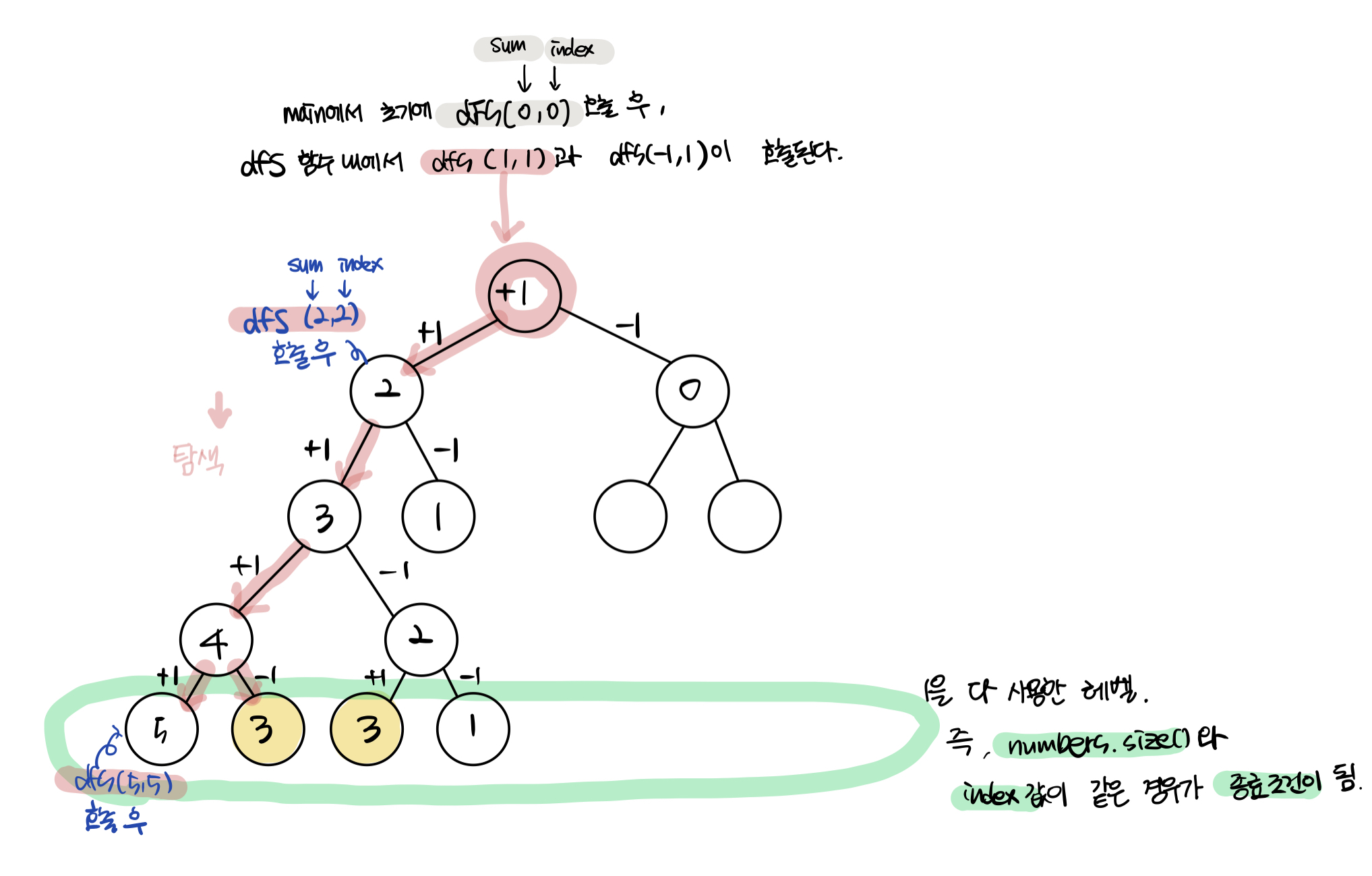
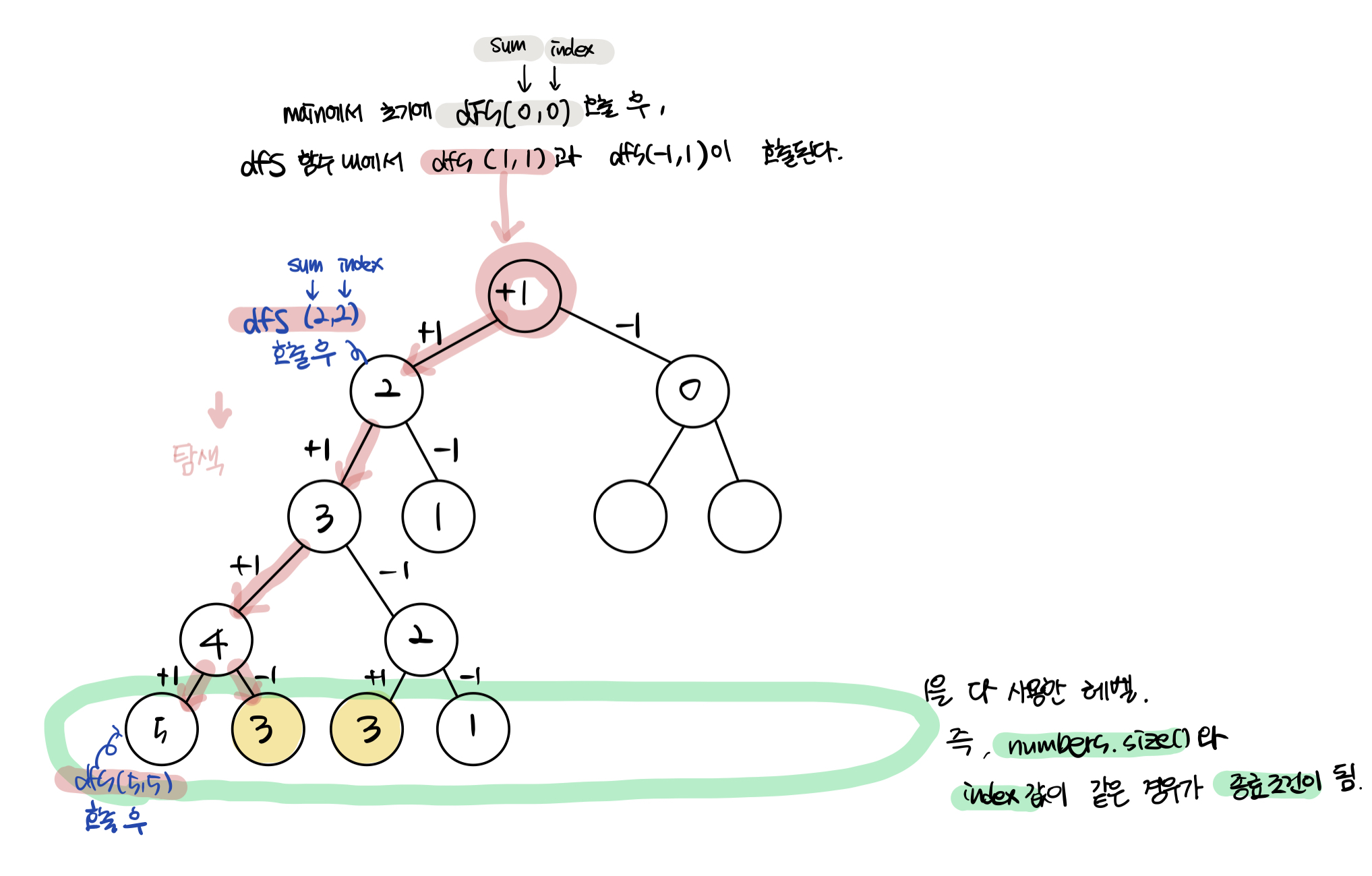
이런식으로 +1로 시작할때의 트리(그래프)를 생각해본다.
또한 전역변수 answer(타겟넘버를 만드는 경우의 수를 저장하는 변수)를 선언하였다고 가정하자.
그래프의 탐색방법 중 DFS로 탐색을 진행해 나가며 numbers 배열에 있는 숫자를 다 사용했을때, 그 때의 노드가 타겟넘버와 같으면 answer에 1을 더해나가며 답을 구한다.
DFS
DFS(Depth First Search, 깊이 우선 탐색) 이란 ❓
루트노드(최상단노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
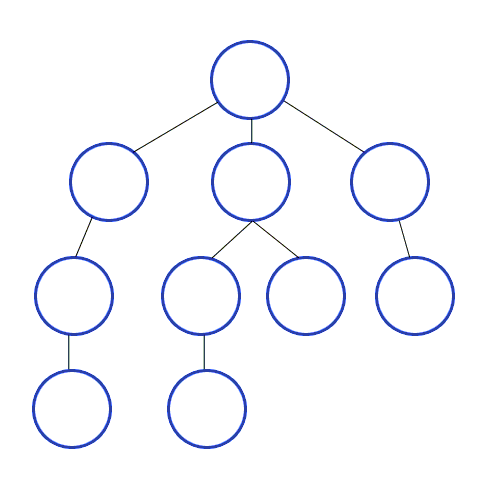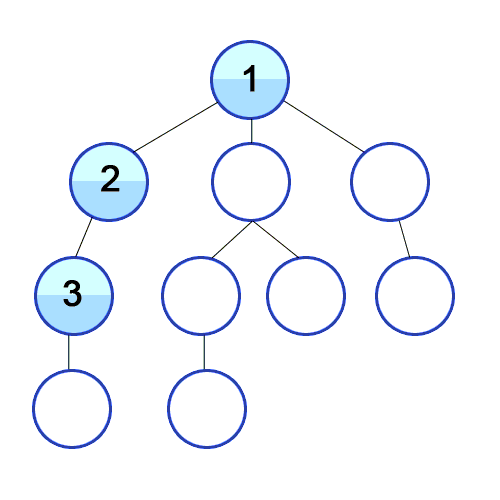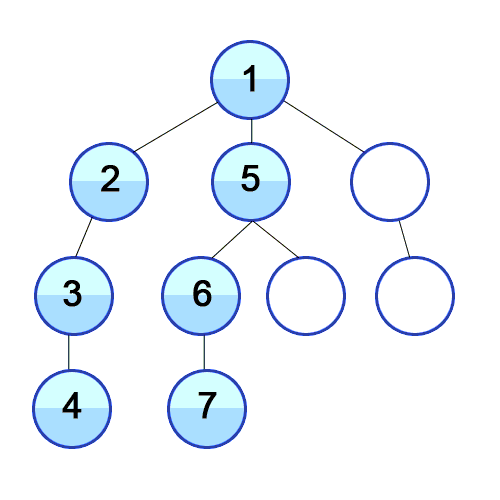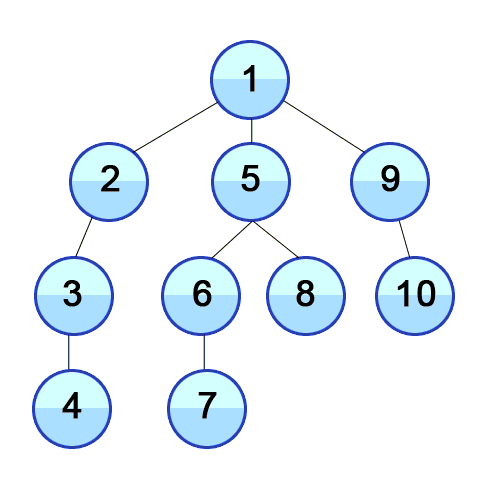
-
미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 (back-tracking) 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
-
즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
✓ DFS를 구현하는 방법은
1. 스택이용
2. 재귀함수
(단, 무한루프에 빠질 수 있기 때문에 각 노드 탐색시에 방문 여부 또한 반드시 체크해줘야함 ❗️)
재귀함수를 작성해보자.
스택을 이용하는 방법보다 재귀함수를 작성하는것이 간단할 것 같아서, 재귀함수를 이용하여 구현했다.
무한루프에 빠지지 않도록, 재귀함수의 종료조건을 먼저 정의해야한다.
-
탐색 시,
numbers벡터의 모든 원소를 사용하였으면 return해야 한다.
(numbers.size()와numbers벡터의 인덱스를 가리키고있는index변수의 값이 같으면numbers벡터의 모든 원소를 사용하였다는 뜻.) -
또한 모든 원소를 사용하였으며 그때의 합이 타겟넘버와 같으면 전역변수
answer에 1을 더해준다.
재귀함수안에서 numbers벡터의 다음원소를 더하는 경우와, 빼는 경우를 나누어 재귀적으로 호출한다.
더하고 빼가며 합을 저장할 sum변수와 numbers벡터의 인덱스를 참조할 index변수가 필요하고, 이들은 재귀함수의 매개변수로 선언되어 각각 호출된 함수에서 사용되어야 한다.
그러면 각각의 함수가 리턴되며 answer 값을 구할 수 있다.
전체 코드
주석 참고해서 이해하시면 좋을 것 같습니다 :)
#include <vector>
using namespace std;
// 전역변수 answer
int answer = 0;
void get_target_number(vector<int> numbers, int target, int sum, int index){
//종료 조건
if (index == numbers.size()){
if (sum == target) {
answer++;
}
// 같지 않을때도 return
return;
}
//종료 조건이 만족되지않으면 계속 탐색
get_target_number(numbers, target, sum + numbers[index], index + 1);
get_target_number(numbers, target, sum - numbers[index], index + 1);
}
int solution(vector<int> numbers, int target) {
get_target_number(numbers, target, 0, 0);
return answer;
}끝 💫