✅ 프로그래머스 N으로 표현
문제링크 : https://programmers.co.kr/learn/courses/30/lessons/42895
숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.
문제 풀이 방법
문제를 처음보자마자 딱히 생각나는 풀이 방법이 없었다.
그래서 입출력 예제에서 규칙을 찾아보기로 하였다.
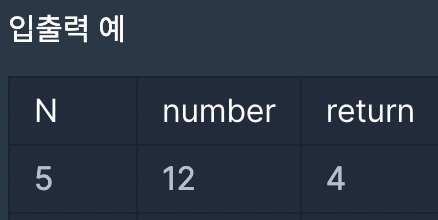
입출력 예제에서 위와 같은 경우에는,
- 5 + 5 + 5/5 + 5/5 = 12 (5를 6번 사용함)
- 55/5 + 5/5 = 12 (5를 5번 사용함)
- (55 + 5) / 5 =12 (5를 4번 사용함)
이렇게 5를 사용하여 12를 만들 수 있는 방법이 3가지 나와있다.
접근방식
1. 우선 5를 이어붙인 결과를 반환할 함수가 필요하다는 것.
N과 idx를 매개변수로 받아서,
idx+1만큼의 개수로 N을 이어붙인 값을 return해준다.
즉 NN(idx==1), NNN(idx==2), NNNN(idx==3)...과 같은 형태를 만들어 준다
int get_Ns(int N, int idx) {
int result = N;
for (int i = 1; i <= idx; i++) {
result = result * 10 + N;
}
return result;
} 2. 예제에서 N이 몇개씩 사용되는지 규칙을 찾아본다.
- 5 + 5 + 5/5 + 5/5 = 12 (5를 6번 사용함)
이 경우에
1개의 5를 이용 + 1개의 5를 이용 + 2개의 5를 이용 + 2개의 5를 이용
총 1개+1개+2개+2개 = 6번 이용됨을 알 수 있다.
이 때, 5가 두번 이용된 5/5의 경우 5가 한번 이용된 경우를 사칙연산으로 결합한 결과임을 알 수 있다.
이 지점에서 DP(동적 계획법)를 떠올릴 수 있다. (다음것이 이전것을 사용한다는 점 ‼️)
DP
DP (동적 계획법, 동적 프로그래밍) 이란 ❓
하나의 문제는 한번만 풀도록 하는 알고리즘
✓ 다음의 가정하에서 이루어진다
1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.
✓ 이미 계산한 결과는 배열에 저장(memoization)하기 때문에 나중에 동일한 계산을 할때는 저장된 값을 반환하기만 하면 됨.
DP에 무엇을 저장할 것인가❓
동적계획법 문제풀이의 핵심은 DP 배열(벡터)에 무엇을 저장할것인가를 정하는 것이다.
위에서 살펴봤듯이,
5가 두번 이용된 5/5의 경우 5가 한번 이용된 경우를 사칙연산으로 결합한 결과임을 알 수 있다.
여기서 N을 i번 이용했을때 만들 수 있는 수들을 DP[i]에 저장하면 될것이라는 생각을 할 수 있다.
즉 DP[i] : i개의 N으로 만들 수 있는 숫자들 이다
실제로 dp배열에 저장해보자.
유의할 것은
DP 배열의 인덱스값은 0부터 시작하므로 실제 이용되는 값보다 1만큼 작다는것!
그리고 아래에서 ㅁ은 사칙연산을 의미한다!
DP[0]: 1개의 N으로 만들 수 있는 수들의 집합은 N한개 밖에 없다.
-> {N} : N1이라고 하자DP[1]: 2개의 N으로 만들 수 있는 수들의 집합은 NN과 N1(N 한개로 만들수있는수)두개끼리 사칙연산한 결과로 이루어져있을것이다.
-> {NN, N1ㅁN1} : N2라고 하자.DP[2]: 3개의 N으로 만들 수 있는 수들의 집합은 NNN과 N1(N 한개로 만들수있는수)와 N2(N 두개로 만들수있는수)를 사칙연산한 결과로 이루어져있을 것이다.
-> {NNN, N1ㅁN2, N2ㅁN1} : N3라고 하자.DP[3]: 4개의 N으로 만들 수 있는 수들의 집합
-> {NNNN, N1ㅁN3, N2ㅁN2, N3ㅁN1} : N4
따라서 식으로 나타내보면,
k번째 DP에는
DP[k]=DP[i]ㅁDP[j](i+j=k)와 NNN...(k개의N)로 이루어져있음을 알 수 있다.
즉, DP배열(vector) 하나하나안에 여러개의 숫자들이 들어있으므로 2차원벡터를 사용할 수 있지만, 조금더 효율을 높이기 위해 unordered_set이라는 자료구조를 사용해 볼 수 있다!
unordered_set
unordered_set은 정렬되지 않은 set이다.
이문제에서 DP벡터안에 각 집합은 정렬될 필요가 없으므로 set보다 unordered_set을 사용하는것이 더 효율적이다.
또한 set자체가 중복을 허용하지 않으므로, 중복 데이터를 자체적으로 제거함으로서 더 효율적으로 사용할 수 있다.
위 문제에서는 작업의 소요시간을 기준으로 오름차순으로 정렬을 하며 큐에 집어넣어야지 최종 답이 최소가 되므로 오름차순으로 정렬을 해야한다.
또한 문제에서 N의 사용횟수가 8보다 클 경우에는 -1을 return하라고 했으므로, DP배열은 8의 크기를 가지면 된다. (왜냐면 DP벡터의 마지막 원소인 DP[7]자체가 N을 8번 사용하여 만들수있는 수들의 집합이므로 DP[8],DP[9]... 는 있어봤자 -1을 return해야하므로 불필요하다.)
vector< unordered_set<int> > DP(8); 이렇게 선언한다.
간단한 사용법
set에 삽입할때는 insert라는 함수를 사용하고
find라는 함수를 사용하여 해당원소가 set에 있는지 확인 가능하다.
-> 이때 해당원소가 없으면 set.end()를 반환한다.
전체 코드
주석 참고해서 이해하시면 좋을 것 같습니다 :)
//https://programmers.co.kr/learn/courses/30/lessons/42895
#include <vector>
#include <unordered_set>
using namespace std;
int get_Ns(int N, int idx) {
// NN(idx==1), NNN(idx==2), NNNN(idx==3)...과 같은 형태만드는 함수
int result = N;
for (int i = 1; i <= idx; i++) {
result = result * 10 + N;
}
return result;
}
int solution(int N, int number) {
if (N == number) return 1; // N과 number가 같다면, N을 한번 사용해서 number를 만들 수 있음
vector< unordered_set<int> > DP(8);
//DP에 저장할 것 -> DP[i] : i개의 N으로 만들 수 있는 숫자들 (set)
DP[0].insert(N); // 한개의 N으로 만들 수 있는 수는 N뿐임
for (int k = 1; k < 8; k++) {
// DP[k]에 NNN...(k+1만큼 반복)과 같은 형태 삽입
DP[k].insert(get_Ns(N, k));
// DP[k]에 사칙 연산의 결과또한 삽입
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++) {
if (i + j + 1 != k) continue;
// i+j+1 == k 일때
for (int a : DP[i]) {
for (int b : DP[j]) {
DP[k].insert(a + b);
// 검사가 필요한 연산들
// (1) 음수 존재하면 안됨
if (a - b > 0)
DP[k].insert(a - b);
DP[k].insert(a * b);
// (2) 0 존재하면 안됨
if (a / b > 0) DP[k].insert(a / b);
}
}
}
}
if (DP[k].find(number)!=DP[k].end()) //DP set에 number에 해당하는 값이 있으면 k+1을 반환
return k + 1;
}
return -1;
}DP를 떠올리는 과정이 어려웠다.ㅠㅠ 분류 DP로 안되어있었으면 더 헤맸을듯 하다...DP넘 어려워 😭
그리구 DP벡터에 삽입할때 연산결과가 음수거나 0인경우를 예외처리하는 것도 까먹지 말아야겠다.
unordered_set사용법도 익혀두는게 좋을 것 같다
끝 💫
참고
https://mind-devlog.tistory.com/2
https://blog.naver.com/ndb796/221233570962