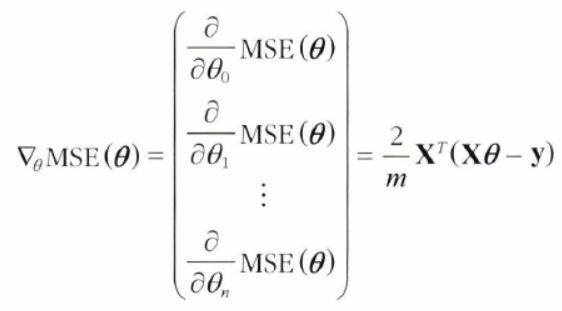[ML] 4. Model Training (1)

1. Linear regression

선형 회귀를 통해 머신러닝의 블랙박스를 이해해보자.

1. 훈련 세트에 가장 잘 맞는 모델 파라미터를 해석적으로 구한다.
   공식으로 직접 계산 (훈련 세트에 대해 비용함수를 최소화)
2. 경사 하강법(GD) 이용 : 반복적인 최적화 방식
   모델 파라미터를 조금씩 바꾸면서 비용함수를 훈련 세트에 대해 최소화
   -> 결국 1의 방법과 동일한 파라미터로 수렴한다.
   GD 종류 : batch GD, mini-batch GD, stochastic GD

1.1 선형 모델 공식화

• 선형 모델 : 입력 특성의 가중치 합 + 편향bias (=절편intercept)(상수) ➡ 예측 생성

선형 회귀 모델의 예측값 $\hat y$ 은 다음과 같이 나타낼 수 있다.

이 식은 아래와 같이 벡터 형태로 표현 가능하다.

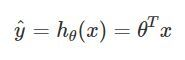
${\theta}$ : 모델의 파라미터 벡터 (${\theta}_0$ ~ ${\theta}_n$)
$x$ : 특성 벡터 ($x_0$ ~ $x_n$) <입력변수 행렬>
${\theta}\cdot x$ : 점곱 dot product
$h_{\theta}$ : 모델 파라미터 ${\theta}$를 사용한 가설함수 hypothesis function
${\theta}^T$ : ${\theta}$의 전치transpose ➡ ${\theta}^T\cdot x$ : 행렬 곱셈
(하나는 열 벡터이고 하나는 행 벡터여야 함, 아니면 전치시켜야 함)

• 모델을 훈련한다 = 훈련 세트에 잘 맞도록 모델 파라미터를 설정한다
• 업데이트를 위해 예측값과 실제값의 차이를 이용한다.
• Root Mean Square Error(RMSE) 이용
• RMSE의 제곱 = Mean Square Error(MSE)
• MSE를 최소화하는 모델 파라미터를 찾는 것이 목표가 된다.

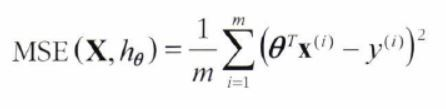
MSE = [($i$번째 예측값 $-$ $i$번째 실제값)의 제곱]의 평균
위 식은 앞으로 $MSE({\theta})$로 표현한다.

1.2 정규방정식 Normal Equation

$\hat{\theta}$ : 비용 함수 $MSE({\theta})$를 최소화하는 ${\theta}$값

---

다음과 같은 선형 회귀 모델을 훈련시켜 보자.

1. (선형처럼 보이는) 데이터 생성

np.random.seed(42)  # 코드 예제를 재현 가능하게 만들기 위해
m = 100  # 샘플 개수
X = 2 * np.random.rand(m, 1)  # 열 벡터
y = 4 + 3 * X + np.random.randn(m, 1)  # 열 벡터

$y = 4 + 3x_1 + 가우시안\_잡음$

${\theta}_0$ (편향bias) = 4
${\theta}_1$ (1번째 모델 파라미터/가중치) = 3
np.random.randn(m, 1) = 가우시안 잡음 (noise)

2. 정규방정식을 통한 $\hat{\theta}$ 계산

theta_best
>> array([[4.21509616],
       [2.77011339]])

▶ ${\theta}_0$=4 ➡ 4.21509616
▶ ${\theta}_1$=3 ➡ 2.77011339
noise 때문에 정확히 재현하지 못함.
(random number가 완벽하게 생성되지 않기 때문에 같아질 수 없음)

3. $\hat{\theta}$ 를 사용한 예측

X_new = np.array([[0], [2]])
X_new_b = add_dummy_feature(X_new)  # 모든 샘플에 x0 = 1을 추가
#X_new_b = np.c_[np.ones((2,1)), X_new]
y_predict = X_new_b @ theta_best
y_predict
>> array([[4.21509616], #시작
       [9.75532293]]) #끝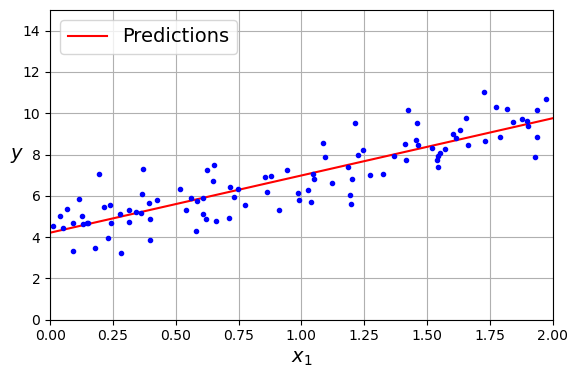

• 사이킷런을 사용하여 선형 회귀 구현

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)

# x=0일 때 y의 좌표(절편intercept), 계수(coefficient) 의미
lin_reg.intercept_, lin_reg.coef_
>> (array([4.21509616]), array([[2.77011339]]))
>> array([[4.21509616], 		[2.77011339]]) #정규방정식

lin_reg.predict(X_new)
array([[4.21509616],
       [9.75532293]])

1.3 계산 복잡도

Computational complexity

• 정규방정식 : $O(n^{2.4})$ 에서 $O(n^{3})$ 사이
  ▶ 특성 수가 두배로 늘어나면, 계산 시간이 $2^{2.4}=5.3$ 에서 $2^3=8$배로 증가
• 사이킷런의 LinearRegerssion() 에서 사용하는 SVD : $O(n^{2})$

2. 경사 하강법 Gradient Descent

일반적인 최적화 알고리즘, large dataset에서 유리
비용 함수를 최소화하기 위해 반복해서 파라미터를 조정해가는 방식

Error (function) = 예측값 - 실제값
Loss (function) = 하나의 데이터에 대한 error (function)
Cost (function) = 데이터의 batch에 대한 평균 error (function)

<빨리 내려가는 방법은 가장 가파른 길을 따라 아래로 내려가는 것이다.>

• 임의의 ${\theta}$ 값에서 시작 : 무작위 초기화 random initialization
• 비용 함수의 미분값 gradient 계산
• gradient (기울기) 가 감소하는 방향으로 진행(업데이트)
• gradient가 0이 되면 최솟값에 도달

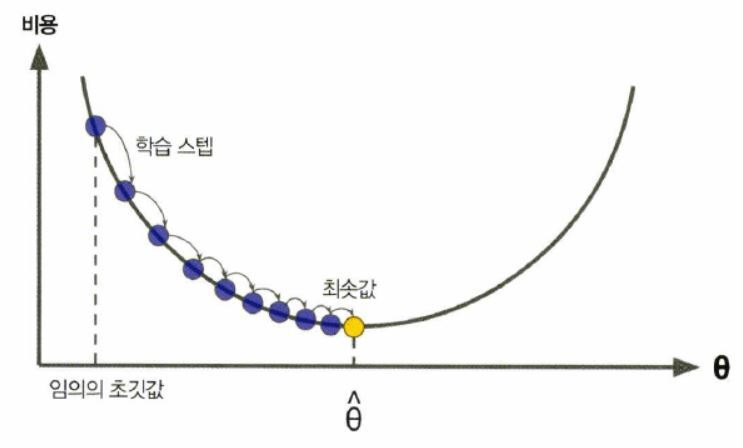
• 스텝의 크기인 학습률Learning Rate 하이퍼파라미터가 중요함

1. 학습률이 너무 작음
   
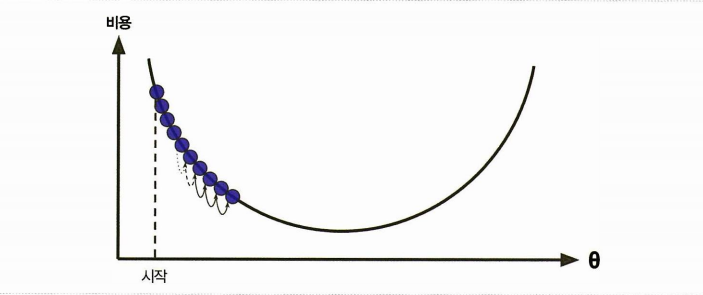
   수렴하기 위해 너무 많은 반복을 진행해야 해서 시간이 오래 걸림

2. 학습률이 너무 큼
   
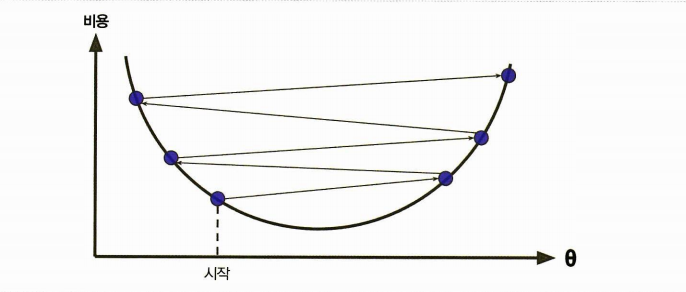
   스텝이 반대편으로 건너뛰어 더 높은 곳으로 가게 될 가능성
   더 큰 값으로 발산하게 만들어 적절한 solution을 찾지 못할 수 있음
   
   
   

• Challenge

1. 무작위 초기화 ▶ 왼쪽에서 시작하면 전역 최소값global minimum 보다 덜 좋은 지역 최소값local minimum에 수렴
2. 오른쪽(평지Plateau)에서 시작하면 시간이 오래 걸리고 일찍 멈추게 되어 전역 최소값global minimum에 도달하지 못함

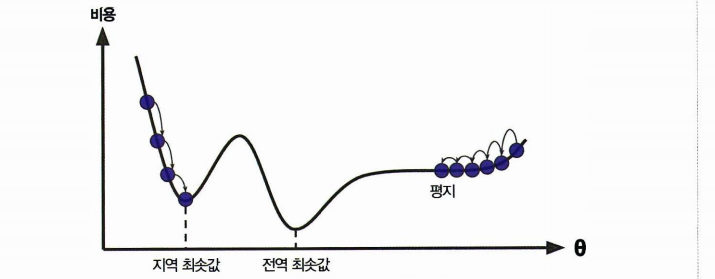
✔ 선형 회귀의 MSE는 항상 볼록 함수Convex
: global minimum이 1개 ➡ GD로 global minimum에 도달할 수 있다.

• 경사 하강법 사용시에는 반드시 모든 특성이 같은 스케일을 가지도록 해야 함
  그렇지 않으면 수렴하는데 더 오랜 시간이 걸린다.
  
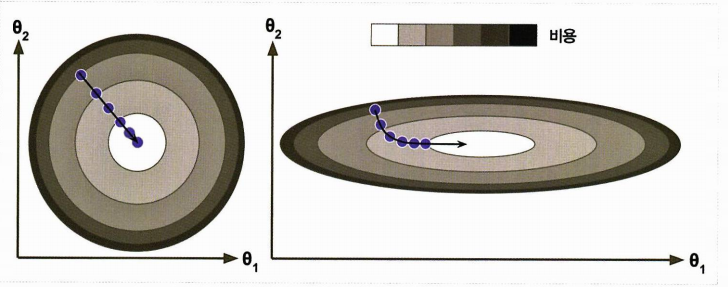
  (왼)스케일 적용한 GD / (오)스케일 적용하지 않은 GD
  
  
  

3. 배치 경사 하강법 Batch GD

• 경사 하강법을 구현하려면 각 모델 파라미터 ${\theta}_j$에 대해 cost function의 gradient를 계산해야 함
  ▶ ${\theta}_j$가 조금 변경될 때 cost function이 얼마나 바뀌는지 계산 : 편도함수partial derivative

• 파라미터 ${\theta}_j$에 대한 비용 함수의 편도 함수
  비용함수를 ${\theta}$에 대해 미분한 값
  

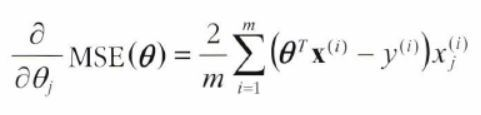
• 모든 차원에 대한 편도함수를 한꺼번에 계산한 gradient 벡터
  비용 함수의 편도 함수는 모델 파라미터마다 한 개씩이다.
  이를 모두 담고 있는 것이 아래의 벡터이다.
  
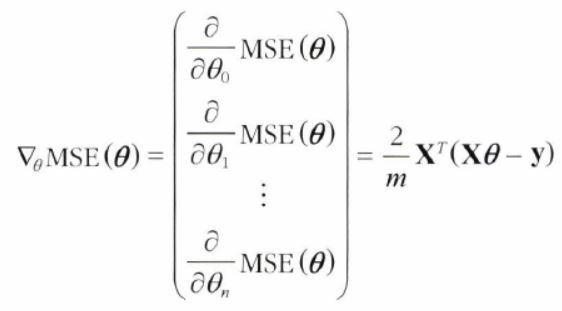
  ✔ 기존 비용 함수에 $X^T$를 곱해준 형태 (우연)
  
  

<배치 경사 하강법>
위의 gradient 벡터 공식 계산을 매 경사하강법 스텝마다 반복한다.
➡ 매 스텝에서 전체 훈련 세트 X에 대해 gradient 계산
➡ 매 스텝에서 훈련 데이터 전체를 사용

• 위로 향하는 gradient 벡터(기울기)가 구해지면 반대 방향인 아래로 가야 함

• 이는 기존 ${\theta}$ 에서, 해당 ${\theta}$ 에서 구한 gradient 벡터(기울기)를 빼서 구할 수 있다.

• 학습률learning rate ($\eta$) 를 곱하여 스텝의 크기 결정

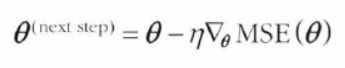
eta = 0.1  # 학습률
n_epochs = 1000
m = len(X_b)  # 샘플 개수

np.random.seed(42)
theta = np.random.randn(2, 1)  # 모델 파라미터를 랜덤하게 초기화

for epoch in range(n_epochs): #전체 차원에 대해 계산
    gradients = 2 / m * X_b.T @ (X_b @ theta - y) #편도함수
    theta = theta - eta * gradients #스텝

# 학습된 모델 파라미터:
theta
>>array([[4.21509616],
       [2.77011339]])

3.1 학습률 Learning rate

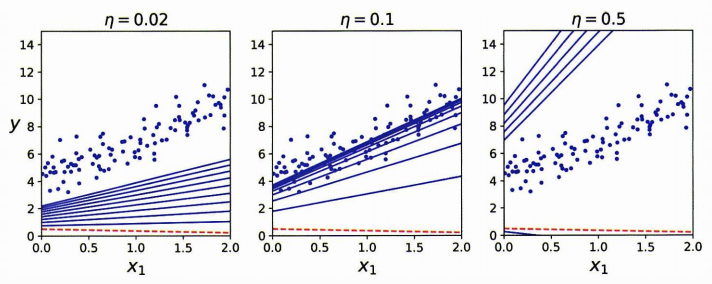
너무 낮은 경우 시간이 오래 걸린다.
적절한 경우 몇 번의 반복iteration으로 최적의 값에 수렴한다.
너무 큰 경우 이리저리로 널뛰다가 발산한다.

• 적절한 학습률 찾기 : 그리드 서치grid search 사용
  ▶ 이때 수렴하는데 너무 오래 걸리는 모델을 막기 위해 반복횟수를 제한해야 함
• 반복 횟수 지정 방법
  1. 반복 횟수를 아주 크게 지정
  2. gradient 벡터가 허용 오차tolerance $\epsilon$ 보다 작아지면 알고리즘 중지