[ML] 4. Model Training (2)

1. 확률적 경사하강법 SGD

Stocastic Gradient Descent
매 스텝에서 한 개의 샘플을 무작위로 선택하고, 그 하나의 샘플에 대한 gradient를 계산한다.

• 배치 경사 하강법보다 훨씬 빠르다.
• 매우 큰 훈련 세트도 훈련시킬 수 있다. (각 iteration 마다 1개의 샘플만 메모리에 할당)

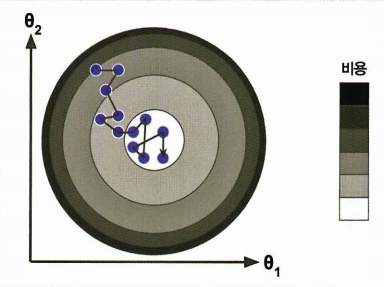
• 확률적Stocastic (=random) : 배치GD 보다 훨씬 불안정함

  • cost function이 최소값에 도달할때까지 위아래로 요동치며 '평균적으로' 감소
  • local minima를 건너뛰게 해줌 (배치GD보다 local minima 찾을 확률이 높음)
  • 최소값에 매우 근접하나, 요동이 지속되면서 최소값에 안착하지 못함
    ➡ 좋은 파라미터가 구해지겠지만, 최적치Optimal는 아님.

  = 지역최소값에서 탈출시켜주지만, 전역 최소값에 도달한다는 보장은 없음.

  ▶ 학습률learning rate를 점진적으로 감소시켜 해결

  • 시작할 때는 학습률을 크게 (수렴을 빠르게 함, 지역 최소값에 빠지지 않게 함)
  • 학습률을 점차 작게 줄여나감 ➡ 전역 최소값에 도달하게 함

  학습 스케줄 Learning schedule
  매 반복iteration 마다 학습률을 조정

  • 학습률이 너무 빨리 줄어들면, 지역 최소값에 갇히거나 최소값까지 가는 중간에 멈춰버릴 수 있다.
  • 학습률이 너무 천천히 줄어들면, 오랫동안 최소값 주변을 맴돌거나 훈련을 너무 일찍 중지하여 지역 최소값에 머무를 수 있다.

n_epochs = 50 # 반복 횟수
t0, t1 = 5, 50  # 학습 스케줄 하이퍼파라미터

def learning_schedule(t):
    return t0 / (t + t1)

np.random.seed(42)
theta = np.random.randn(2, 1)  # random initialization

for epoch in range(n_epochs): # 한 반복 = epoch, 1epoch에 m번 되풀이됨
    for iteration in range(m): # m = 훈련 세트에 있는 샘플의 개수
        random_index = np.random.randint(m)
        xi = X_b[random_index : random_index + 1]
        yi = y[random_index : random_index + 1]
        gradients = 2 * xi.T @ (xi @ theta - yi)  # SGD의 경우 m으로 나누지 않습니다
        eta = learning_schedule(epoch * m + iteration)
        theta = theta - eta * gradients

theta
>> array([[4.21076011],
       [2.74856079]])

스텝이 불규칙하게 진행하는 것을 확인할 수 있다.

• 무작위 초기화 -> 한 에포크에서 여러번 선택되는 샘플이 있을 수도 있고, 한 번도 선택되지 않은 샘플이 있을 수도 있다.
• 훈련 세트를 shuffling -> 차례대로 선택 -> 다음 epoch에 다시 shuffling ...
  • 사이킷런의 SGDClassifier, SGDRegressor가 사용하는 방식
  • 보통 더 늦게 수렴된다.

사이킷런 SGDRegressor

• 선형 회귀
• 기본값으로 MSE cost function을 최적화함

from sklearn.linear_model import SGDRegressor

sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.01,
                       n_iter_no_change=100, random_state=42)
sgd_reg.fit(X, y.ravel())  # fit()이 1D 타깃을 기대하기 때문에 y.ravel()로 씁니다

sgd_reg.intercept_, sgd_reg.coef_
>> (array([4.21278812]), array([2.77270267]))

• max_iter=1000 : 1000번의 epoch
  ✔ 1번의 epoch에서 m개 샘플에 대해 업데이트(m회 iteration)
• tol=1e-3 : 한 에포크에서 0.001보다 적게 손실이 줄어들 때까지 실행
• penalty=None : 규제 사용 X
• eta0=0.01 : 초기 학습률 0.01, default 'invscaling' 으로 사용

  invscaling 학습률 $\eta^{(t)} = \frac{eta0}{t^{power\_t}}$
  t : 반복횟수
  power_t : default 0.25
  eta0 : default 0.01

2. 미니배치 경사하강법 Mini-batch GD

• 미니배치 : 샘플 여러 개를 묶어둔 임의의 작은 샘플 세트
• 미니배치에 대해 gradient 계산

경사 하강법 정리

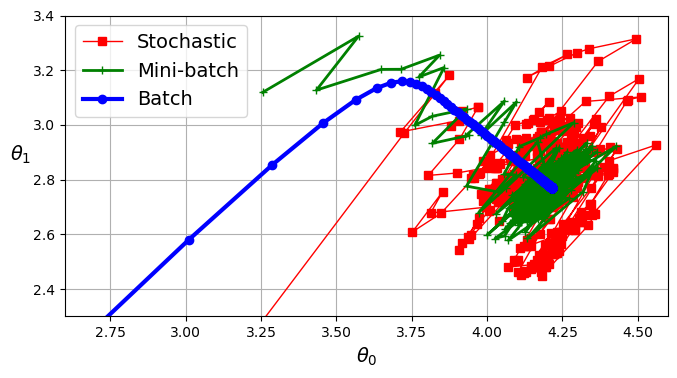
모두 최솟값 근처에 도달함

• 배치 : 실제 최솟값에 멈춤 ✔ 매 스텝에서 많은 시간이 소요됨
• SGD, 미니배치 : 최솟값 근처에서 맴돌고 있음 ✔ 적절한 learning schedule 사용시 최솟값에 도달 가능

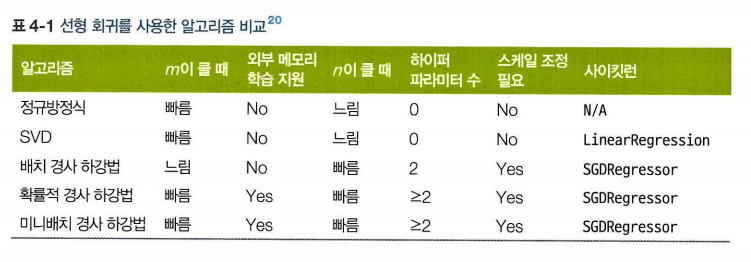
(m : 샘플의 수, n : 특성의 수)

---

3. 다항 회귀 Polynomial Regression

데이터가 직선이 아닌 복잡한 곡선의 형태(비선형 데이터)일 때

각 특성의 거듭제곱을 새로운 특성으로 추가하고, 이 확장된 특성의 비선형 데이터셋에 선형 모델을 훈련시킨다.

• 2차방정식으로 비선형 데이터 생성

np.random.seed(42)
m = 100 #샘플의 개수
X = 6 * np.random.rand(m, 1) - 3 #약간의 noise 포함
y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1)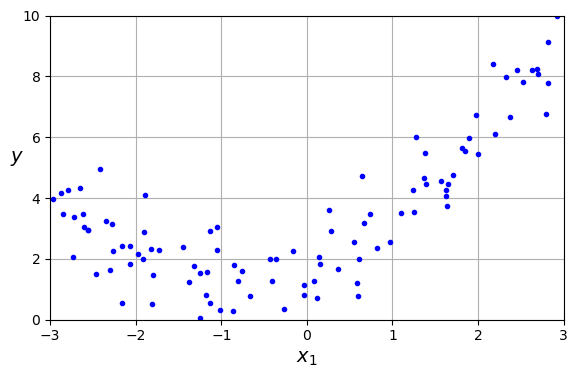

• 사이킷런의 PolynomialFeatures 사용
  : training set의 각 특성을 제곱하여 새로운 특성으로 추가한다.
  ➡ 일종의 변환기 역할, fit_transform() method 사용

from sklearn.preprocessing import PolynomialFeatures

poly_features = PolynomialFeatures(degree=2, include_bias=False) #2차, 편향 포함x
X_poly = poly_features.fit_transform(X) #x^2을 새로운 특성으로 추가
X[0] # 기존 특성 x1
>> array([-0.75275929])
X_poly[0] # 특성 x1, x2 포함 (x2 = x1^2 기존 특성의 제곱)
>> array([-0.75275929,  0.56664654])

lin_reg = LinearRegression()
lin_reg.fit(X_poly, y) # 2개의 입력 특성에 대한 선형 회귀
lin_reg.intercept_, lin_reg.coef_ # 편향/절편, 계수(특성의 가중치)
>> (array([1.78134581]), array([[0.93366893, 0.56456263]]))

• 특성 : $x_1, x_1^{2}$
• 계수(특성의 가중치) : 0.93, 0.56
• 편향bias/절편intercept : 1.78
  ▶ (예측값) $\hat y = 0.56x_1^2 + 0.93X_1 + 1.78$
  ▶ (실제값) $y = 0.5x_1^2 + 1.0x_1 + 2.0 + Gaussian \_noise$
  

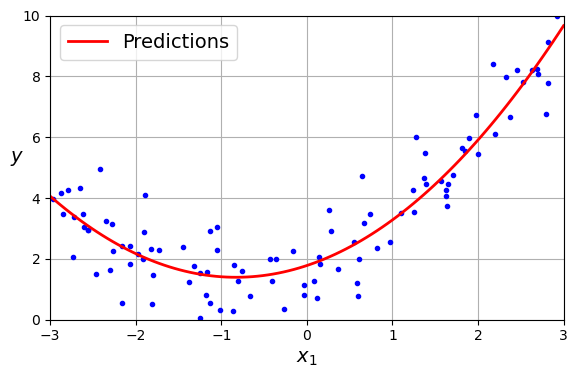
• PolynomialFeatures가 (주어진 차수까지) 특성간의 모든 교차항을 추가하므로 다항 회귀는 여러 개의 특성 사이의 관계를 찾을 수 있다.
  ex. 특성 $a, b$ ▶ degree=3 으로 PolynomialFeatures 적용
  : $a^2, a^3, b^2, b^3$ 뿐만 아니라 $ab, a^2b, ab^2$ 도 특성으로 추가함

4. Learning Curve

다항 회귀의 차수가 높아질수록 훈련 데이터에 잘 맞추려고 하기 때문에 구불구불하게 나타난다.

• 1차, 2차, 300차 다항회귀

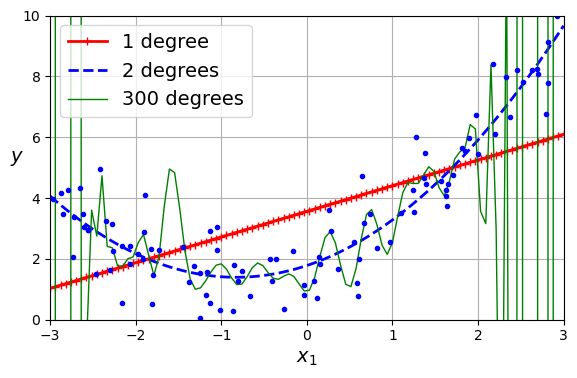
• 1차는 과소적합 / 300차는 과대적합 / 2차는 적당함

  ✔ 교차 검증 cross validation
  training set에서 성능이 좋지만 교차 검증 점수가 나쁘다면 과대적합
  양쪽 모두 좋지 않다면 과소적합
  ▶ training set에서의 accuracy와 validation set에서의 accuracy를 비교한다.
  
  ✔ 학습 곡선
  훈련 세트 크기에 따른 훈련 세트와 검증 세트의 성능(비용함수)을 보여준다.
  ▶ 훈련 세트에서 크기가 다른 subset을 만들어 모델을 여러번 훈련

4.1 과소적합 Underfitting

단순 선형 회귀 모델 Linear regression 의 학습 곡선

✔ 과소적합 underfitting 모델

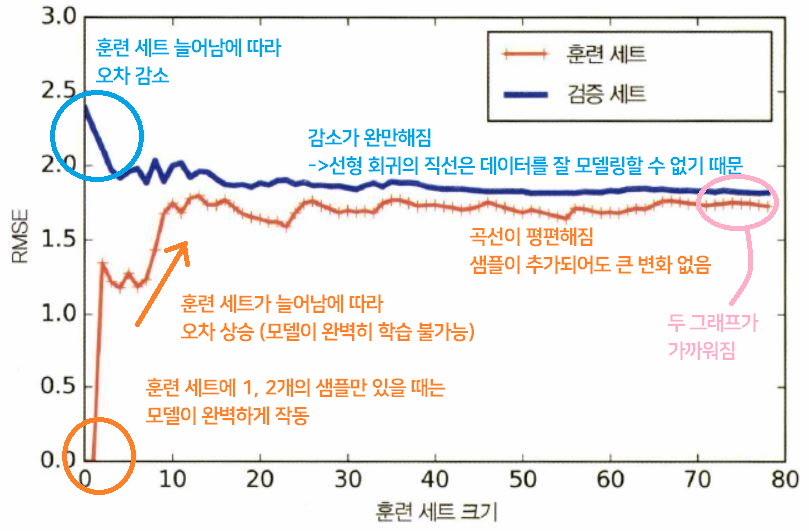
Underfitting
▶ 두 곡선이 수평한 구간을 만들고, 꽤 높은 오차에서 가까이 근접
▶ 훈련 샘플을 추가해도 효과 X > 더 복잡한 모델을 사용하거나, 나은 특성을 선택해야 함

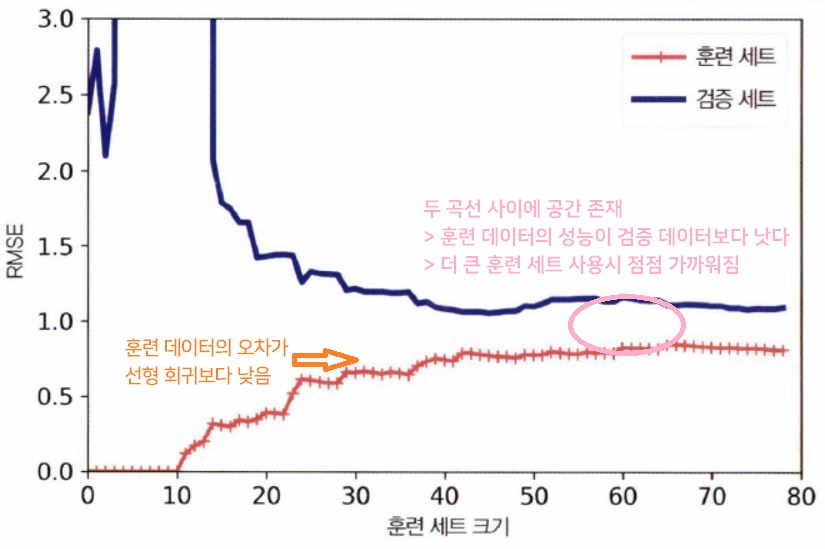
4.2 과대적합 Overfitting

✔ 과대적합 overfitting 모델

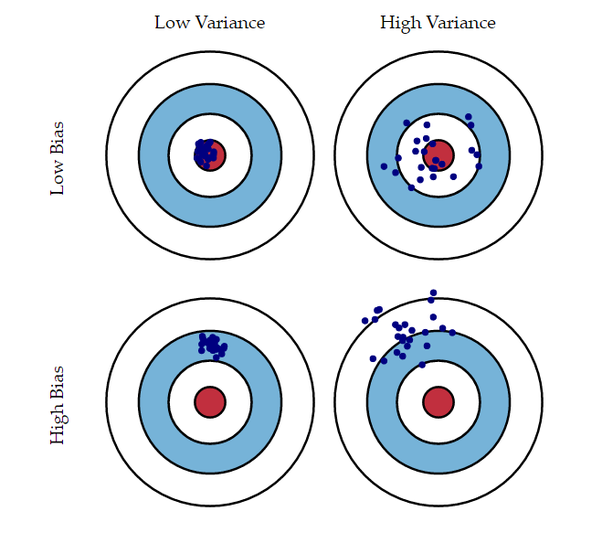
4.3 편향/분산 트레이드오프

모델의 일반화 오차는 세 가지 종류의 오차의 합으로 표현 가능

이때의 편향bias는 선형 모델의 편향bias(절편intercepts)와는 다르다.

✅ 예측값들과 정답이 멀리 떨어져 있으면 편향bias이 크다
✅ 예측값들이 자기들끼리 대체로 멀리 흩어져있으면 분산variance이 크다

<일반화 오차 3가지 : 편향bias, 분산variance, 줄일 수 없는 오차irreducible error>

• 편향bias
  잘못된 가정으로 인한 것 (ex. 데이터가 실제로는 2차인데, 선형으로 가정)
  높은 편향 > 과소적합underfitting 위험

• 분산variance
  훈련 데이터의 작은 변동에 모델이 과도하게 민감하다.
  자유도가 높은 모델(ex.고차 다항회귀 모델) > 높은 분산 > 과대적합overfitting

• 줄일 수 없는 오차irriducible error
  데이터 자체에 있는 노이즈 때문에 발생 > 노이즈를 제거하는 것이 유일한 방법

Bias/Variance Tradeoff
✔ 모델의 복잡도가 커지면 variance가 늘어나고, bias는 줄어든다.
: 예측값들끼리 정답에 가까운 부근에서 멀리 흩어지게 된다.
✔ 모델의 복잡도가 줄어들면 bias가 늘어나고, variance가 줄어든다.
: 예측값들이 정답에서 멀어지지만 서로 모여 있다.

---

이 내용 참고하기 편향과 분산