[ML] 9. Unsupervised Learning (1)

0. Unsupervised learning

레이블, 즉 정답이 없는 데이터를 사용하는 학습

• clustering : 비슷한 샘플을 클러스터cluster로 모음 (그룹화)
• outlier detection : 정상 데이터를 학습하고, 비정상 샘플을 감지하는 데 사용
• density estimation : 데이터셋 생성의 random process에서 확률밀도함수(PDF) 추정. 밀도가 낮은 영역의 샘플이 outlier일 가능성이 높다. (outlier detection에 사용)

1. Clustering

비슷한 샘플을 구별해 하나의 클러스터cluster로 할당 (그룹화)

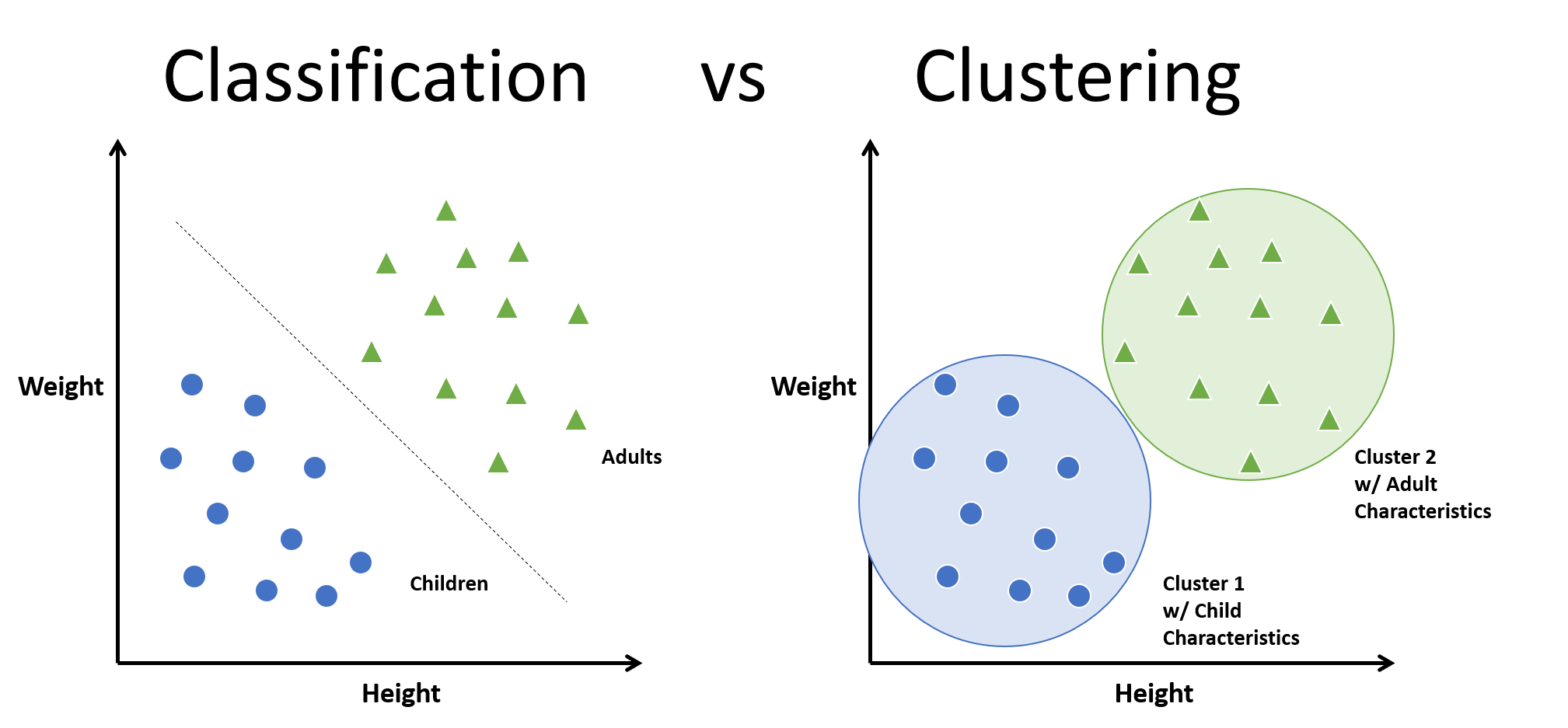
• 분류Classification와 군집화Clustering을 혼동하지 말자.
  
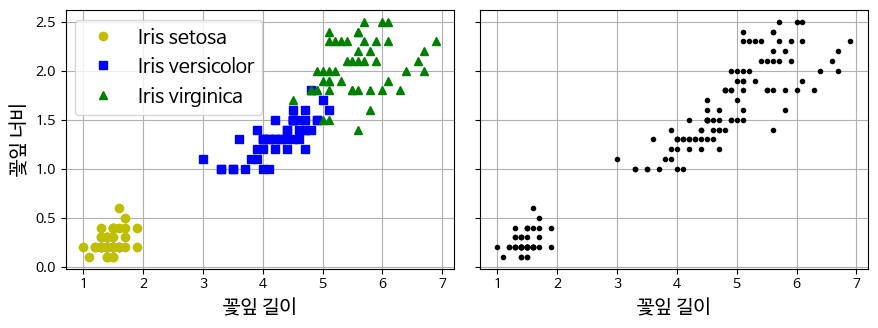
  (왼) 분류 : 지도학습. 각 샘플이 레이블링 되어있으므로, 품종(클래스)이 구분되어 나타나 있음
  (오) 클러스터링 : 레이블이 없음 ➡ 알고리즘이 클러스터를 감지하여 그룹화
• 비슷한 특성에 따라서 그룹화를 하지만, 각 그룹의 구체적 의미(이름 등)는 모르는 상태가 된다.
  

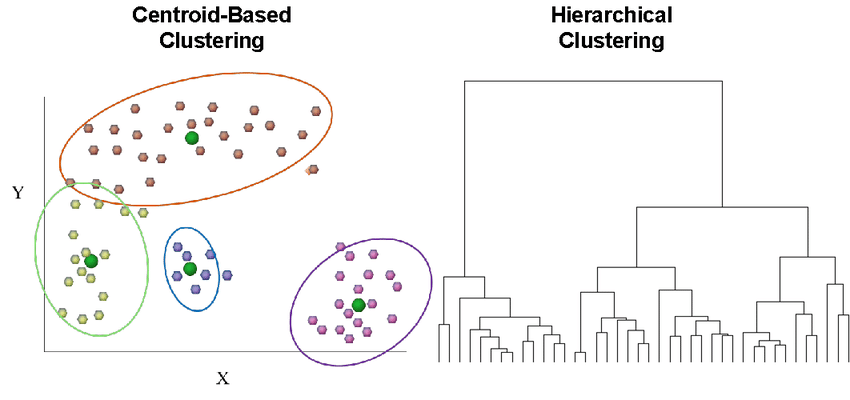
클러스터링의 보편적인 정의는 없고, 알고리즘과 상황에 따라 다름

• 센트로이드centroid 라는 특정 포인트를 중심으로 모인 샘플을 그룹화하는 경우
• 샘플이 밀집되어 연속된 영역을 찾는 경우
• 계층적hierarchical으로 클러스터 안의 클러스터를 찾는 경우
  

다양한 레퍼런스(기준?)에 따라서 클러스터링 결과는 크게 달라짐

• 클러스터링 사용 분야

1. 고객 분류 customer segmentation
   고객을 구매이력이나 웹사이트 내 행동 등을 기반으로 클러스터로 모은다.
   고객 그룹마다 제품 추천이나 마케팅 전략을 다르게 적용 가능 (추천 시스템)

2. 데이터 분석
   새로운 데이터셋을 분석할때 클러스터링 후 각 클러스터를 따로 분석
   클러스터 내부의 유사성, 클러스터 간의 차이점 등을 쉽게 파악 가능

3. 차원 축소 기법dimentionality reduction technique
   클러스터링된 데이터셋에서, 각 클러스터들에 대한 각 샘플의 친화성affinity 측정 가능
   ✅ 해당 샘플이 각 클러스터와 얼마나 가까운지 측정 (유사도 증가=affinity 증가)

   • 각 샘플의 특성 벡터 $x$는 cluster affinities의 벡터로 바꿀 수 있음
   • k개의 클러스터가 있다면, 이 벡터는 k차원이 됨
   • 일반적으로 원본 특성 벡터보다 훨씬 저차원이지만 충분한 정보를 가질 수 있음

4. 이상치 탐지 anomaly detection
   모든 클러스터에 affinity가 낮은 샘플은 이상치anomaly일 가능성이 높음
   ✅ 특정 클러스터에 속하지 못하는 샘플들. 또 이러한 샘플들이 하나의 클러스터로 모이지도 못할 때 anomaly로 판단된다
   제조 분야에서 결함을 감지할 때나 부정 거래 감지(일반적인 사용 패턴과 다른 경우를 탐지)에 활용

5. semi-supervised learning
   레이블링된 데이터가 적고, 레이블이 없는 데이터가 다수인 경우
   unsupervised : 클러스터링을 진행한 후에 같은 클러스터 안에 있는 unlabeled 데이터를 labled 데이터의 레이블로 카피한다.
   ➡ 동일한 클러스터에 있는 모든 샘플에 레이블을 전파
   supervised : 레이블이 생긴 데이터로 지도학습 진행

6. 검색 엔진
   제시된 reference 이미지와 비슷한 이미지를 찾아줌
   - 데이터베이스의 모든 이미지를 클러스터링
   - reference 이미지의 클러스터를 찾아 해당 클러스터의 모든 이미지를 반환
   
   7.이미지 분할
   색을 기반으로 이미지의 픽셀을 클러스터로 모으고, 각 픽셀을 해당하는 클러스터의 평균 색으로 바꾼다. (segmentation)
   ✅ 하나의 cluster ➡ 하나의 object로 변환
   이미지에 있는 색상 종류를 줄이고 물체의 윤곽을 감지하기 쉬워진다.

1.1 K-Means

데이터가 모여있는 곳(blob)의 중심을 찾고, 가장 가까운 blob에 샘플을 할당한다.

• n_clusters = k : 알고리즘이 찾을 클러스터 개수 k를 지정
  ✔ 특징을 모르기 때문에 미리 결정하기 어려움

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

k = 5
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X) #클러스터링 진행

• 클러스터에서 각 샘플이 갖는 레이블label은 해당하는 클러스터의 인덱스이다.
  이는 특별한 의미를 갖는 것이 아닌 클러스터의 순서정도로 이해하면 된다. (❗❗ 분류에서 쓰이는 정답 레이블이 아님 ❗❗)
• kmeans.labels_ : 훈련된 샘플의 레이블을 가지고 있음 (=y_pred)

y_pred
# 각 샘플마다 0~4의 클러스터 중 해당하는 예측 클러스터를 반환
# 같은 레이블(인덱스)를 갖는 샘플은 같은 클러스터에 속함
>> array([4, 0, 1, ..., 2, 1, 0], dtype=int32)

y_pred is kmeans.labels_
>> True

• kmeans.cluster_centers_ : 센트로이드 확인

kmeans.cluster_centers_
# 5개 클러스터에서 각 centroid의 x1, x2 좌표 반환
>> array([[-2.80389616,  1.80117999],
         [ 0.20876306,  2.25551336],
         [-2.79290307,  2.79641063],
         [-1.46679593,  2.28585348],
         [-2.80037642,  1.30082566]])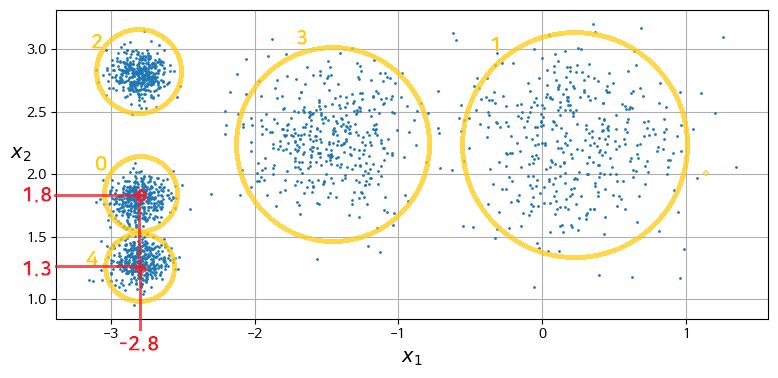

• kmeans.prediction : 새로운 샘플을 가장 가까운 센트로이드의 클러스터에 할당

X_new = np.array([[0, 2], [3, 2], [-3, 3], [-3, 2.5]])
kmeans.predict(X_new)
# 4개의 샘플에 대한 클러스터 인덱스(레이블) 반환
>> array([1, 1, 2, 2], dtype=int32)

1.2 k-means cluster decision boundary

보로노이 다이어그램Voronoi tessellation

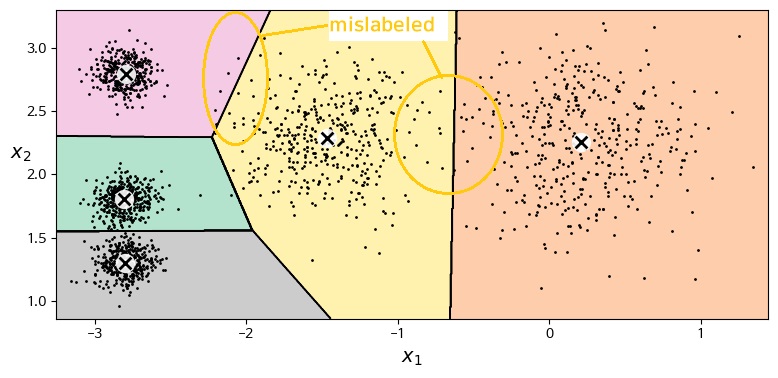
• 몇 개는 잘못된 클러스터로 포함됨(mislabeled)
• 클러스터의 크기가 많이 다르면 잘 작동하지 않음
  (새로운 샘플과 클러스터까지의 거리만을 고려하기 때문에)

• hard clustering
  각 샘플에 대해 가장 가까운 센트로이드 선택
• soft clustering
  샘플이 각 클러스터에 속할 score 부여
  ✅ score
  • 샘플과 센트로이드 사이의 거리
  • 유사도 점수(or affinity) : Gaussian Radial Basis Function
    ➡ 단순 거리가 아닌 복잡한 방법으로 유사도를 측정함

• kmeans.transform() : 샘플과 센트로이드 사이의 거리 반환

X_new = np.array([[0, 2], [3, 2], [-3, 3], [-3, 2.5]])

kmeans.transform(X_new).round(2)
>> array([[2.81, 0.33, 2.9 , 1.49, 2.89],
         [5.81, 2.8 , 5.85, 4.48, 5.84],
         [1.21, 3.29, 0.29, 1.69, 1.71],
         [0.73, 3.22, 0.36, 1.55, 1.22]])

hard vs. soft clustering

• Soft
  kmeans.transform() : 각 클러스터에 대한 score만을 제공
  ➡ 이를 이용하는 방법은 필요에 따라 결정한다. (가장 먼 것, 가장 가까운 것, ...)
• Hard
  kmeans.prediction : 샘플의 클러스터를 결정해서, 해당하는 클러스터의 레이블(인덱스)를 반환한다.

1.3 k-means algorithm

1. 센트로이드 랜덤하게 선정(초기화)
2. 선정한 센트로이드를 기준으로 클러스터를 나눔(샘플에 레이블 할당)
3. 나눠진 클러스터를 바탕으로 다시 센트로이드 업데이트
4. 2와 3을 반복(센트로이드의 이동이 특정 tolerance 이하가 되면 즉, 거의 움직이지 않게 되면)

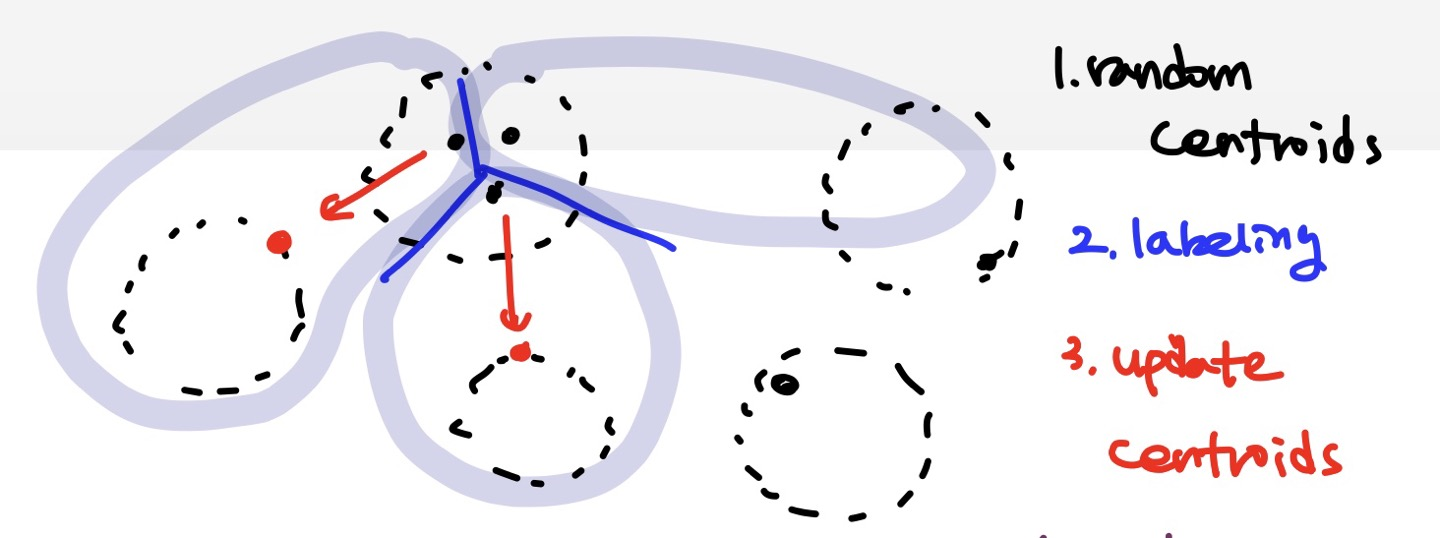
계산 복잡도

• 데이터가 클러스터링할 수 있는 구조로 되어 있다면(군집 존재), 샘플 개수 m, 클러스터 개수 k, 차원 개수 n에 선형적이다.
  ✅ 차원 개수 n = 입력 특성의 개수
  특성 개수가 늘어나면 거리를 계산할 때의 복잡도가 증가한다.
• 그렇지 않은 경우(데이터가 균일하게 분포되어있는 경우 or 한곳에 모두 몰려있고 나머지는 흩어져있는 경우 등)에는, 샘플 개수에 대해 지수적으로 증가할 수 있음 (클러스터링에 적합하지 않은 데이터)

• 수렴은 보장되나, 센트로이드 초기화에 따라 지역 최적점local optimum에 수렴할 수 있다. (최적이 아닌 솔루션)

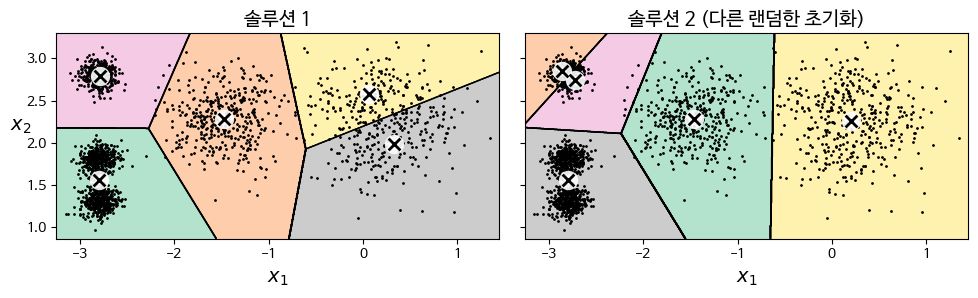
센트로이드 초기화 메소드가 솔루션에 영향을 미치는 것은 사실이나, 특정한 무작위 초기화를 사용했을 때 항상 나쁜 솔루션이 나오는 것은 아님. (운이 나쁜 경우였던 것)

1.4 centroid initialization method

• 다른 군집의 알고리즘을 먼저 실행하는 등의 방법으로 센트로이드 위치를 근사하게 알아낸다.
  • init : 센트로이드 리스트를 담은 넘파이 배열
  • n_init : 랜덤 초기화 횟수 (default=10)

good_init = np.array([[-3, 3], [-3, 2], [-3, 1], [-1, 2], [0, 2]])
kmeans = KMeans(n_clusters=5, init=good_init, n_init=1, random_state=42)
kmeans.fit(X)

• 미리 알고있지 않은 경우,
  : n_init = n 으로 설정하고 fit() 호출시 k-means 알고리즘이 n번 실행된다.
  ➡ n개의 센트로이드 셋을 설정하고, 각각 클러스터링 알고리즘을 진행한다.
  ➡ 이 중의 최선의 솔루션을 반환한다.

결과 비교 지표 : 이너셔inertia

• 각 샘플과 가장 가까운 센트로이드 사이의 제곱 거리의 합 (Mean Squared Distance)
• 클러스터의 센트로이드와 각 샘플의 거리가 가까울수록 클러스터링이 잘 진행된 것이다.

kmeans.inertia_ # 거리 반환 (값이 작을수록=거리가 가까울수록 좋다)
>> 211.59853725816834

kmeans.score(X) # 음수 inertia 반환 (값이 클수록 좋다)
-211.59853725816836

1.5 k-Means++

• 다른 센트로이드와 거리가 먼 센트로이드를 선택
• 특정 센트로이드들이 서로 가깝게 붙어 있어서 최적이 아닌 솔루션에 빠지는 경우가 생기는데, 이러한 상황을 줄인다.

1. 데이터셋에서 무작위로 균등하게 센트로이드 $c^{(1)}$ 선택
2. $D(x^{(i)})^2 / \sum_{j=1}^{m}D(x^{(j)})^2$
   : 샘플 x^{(i)}와 이미 선택된 가장 가까운 센트로이드까지의 거리의 제곱
   / 모든 샘플에 대해 자신과 가장 가까운 센트로이드와의 거리의 제곱을 모두 합한 것
   ✅ 현재 센트로이드와 거리가 먼 새로운 센트로이드를 선택하는 것
   거리가 가까워짐 > 확률이 낮아짐 > 새로운 센트로이드로 선택될 가능성 낮아짐
   거리가 멀어짐 > 확률이 높아짐 > 새로운 센트로이드로 선택될 가능성 높아짐
3. k개의 센트로이드가 선택될때까지 반복
   ➡ 기존 센트로이드가 k개 존재하므로, 각 센트로이드마다 모든 샘플에 대해 위의 방법을 진행한다.
4. 선택된 k개의 센트로이드로 k-means 알고리즘 진행

• (default) init = 'k-means++'
• (기존방식) init = 'random' : 초기 센트로이드를 랜덤하게 선택

---

[머신러닝] K-평균(K-Means) 알고리즘