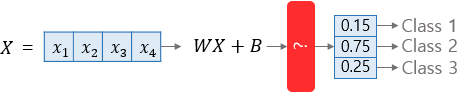1. Regulalization
규제(모델을 제한) ➡ 자유도를 낮춘다 ➡ overfitting을 막는다!
선형 회귀 : 모델의 가중치를 제한함
다항 회귀 : 다항식의 차수를 감소시킴
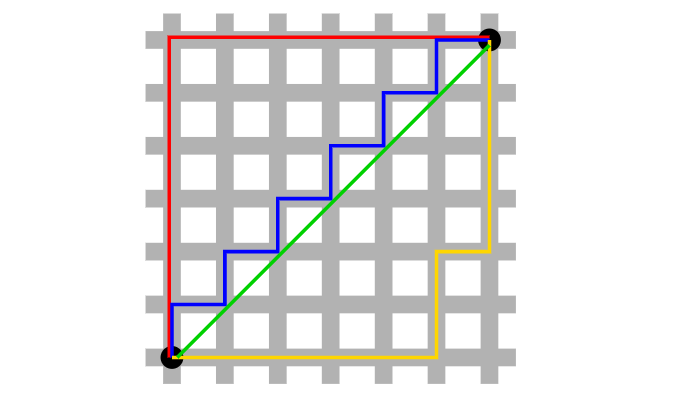
노름 norm : 벡터의 크기를 나타냄
위 그림에서 빨강, 파랑, 노랑처럼 최단 경로를 찾는 방법이 L1 norm (Lasso)
초록처럼 최단 거리로 계산하는 방법이 L2 norm (Ridge)
이전까지 선형 회귀는 비용 함수 MSE, 즉 실제값과 예측값의 차이를 최소화하는 것만을 목표로 했다.
이 경우 훈련 데이터에 매우 적합하게 되어 극단적으로 오르락내리락하는 그래프가 생성되고, 이때 회귀 계수()의 값이 매우 크게 나타난다.
ex.
이 경우 변동성이 커져서 검증 세트에서는 성능이 떨어지는 것이다.
따라서 회귀 계수()의 값이 포함된 규제항을 비용 함수에 추가한다.
이 비용 함수를 최소화하는것이 목표가 되면, 오차를 줄이는 방법과 회귀 계수를 줄이는 방법이 균형을 이루게 한다.
➡ 회귀 계수의 크기를 제어해 overfitting을 막는 방법.
1.1 Ridge Regression
L2 규제가 추가된 선형 회귀
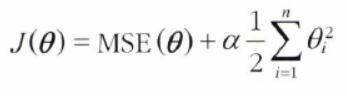
-
비용 함수 에 규제항 을 추가
➡ 규제항 : 하이퍼파라미터 알파 * (가중치 제곱) 의 합 (L2 규제)
✔ 에서 시작 : (bias)는 규제되지 않음 -
hyperparameter : 모델을 얼마나 규제할지 조절
- 이면 규제하지 않는 것이므로 선형회귀와 동일해짐
- 가 매우 크면 모든 가중치가 0에 가까워진다. (0이 되지는 않음)
: 데이터의 평균을 지나는 수평선이 됨
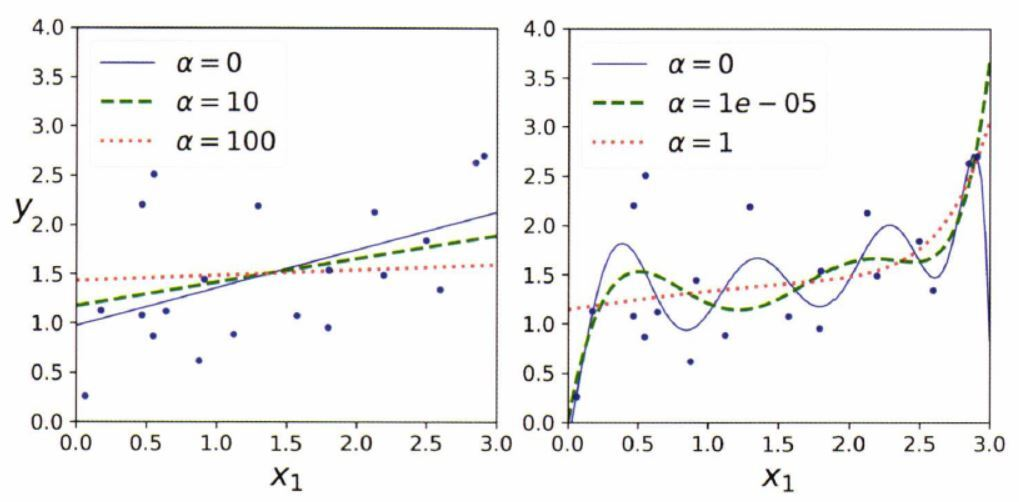
(왼) 선형회귀 : 를 증가시킬수록 수평선에 가까워진다.
(오) 다항회귀 : 를 증가시킬수록 직선에 가까워진다.
✔ 증가 > 분산은 줄어들고, 편향은 커진다.
- 정규방정식
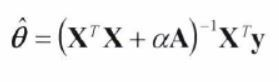
= 맨 위쪽의 원소(=편향bias)가 0인 (n+1)*(n+1)의 단위행렬
- 사이킷런
Ridge
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=0.1, solver="cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
>> array([[1.55325833]])- SGD에 L2 규제 추가
:penalty = 'l2'로 지정 ➡ 노름의 제곱을 2로 나눈 규제항 추가(=릿지 회귀)
sgd_reg = SGDRegressor(penalty="l2", alpha=0.1 / m, tol=None,
max_iter=1000, eta0=0.01, random_state=42)
sgd_reg.fit(X, y.ravel()) # fit()은 1D 타겟을 기대하므로 y.ravel()을 사용
sgd_reg.predict([[1.5]])
>> array([1.55302613])1.2 Lasso Regression
L1 규제가 추가된 선형 회귀
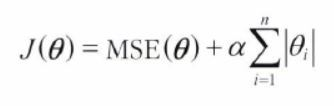
- 비용 함수 에 규제항 을 추가
➡ 규제항 = 하이퍼파라미터 알파 + (가중치 절대값)의 합 (L1 규제)
✔ 동일하게 은 규제되지 않음
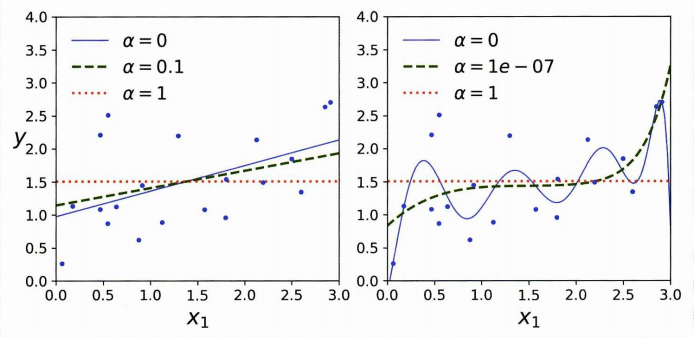
- 덜 중요한 특성의 가중치를 제거 (가중치=0)
➡ (우) 점선 : 10차 다항 회귀 모델이나, 차수가 높은 특성의 가중치가 모두 0이 되어 3차방정식처럼 보임 - 자동으로 특성 선택을 하고, 희소한sparse 모델을 만든다.
➡ 0이 아닌 특성의 가중치가 적음 (대부분의 가중치가 0)
특성 선택을 통해 완전히 제외되는 특성이 생긴다.
이를 통해 모델을 이해하기가 쉬워지고, 해당 특성이 이 모델에서 중요한 특성인지 알 수 있다.
- 라쏘의 비용함수는 일 때 미분가능하지 않다.
이때 경사하강법을 사용하기 위해 subgradient 벡터 g를 사용
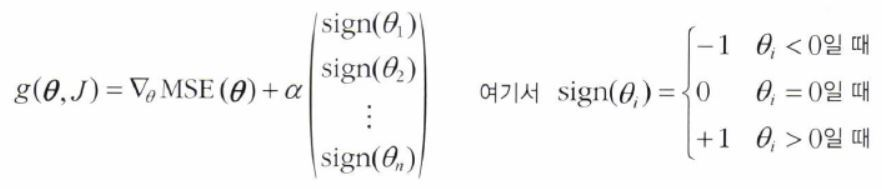
- 사이킷런
Lasso
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
>> array([1.53788174])- SGD에 L1 규제 추가
:penalty = 'l1'로 지정 ➡ 노름의 규제항 추가(=라쏘 회귀)
sgd_reg = SGDRegressor(penalty="l1")
sgd_reg.fit(X, y_ravel())
sgd_reg.predict([[i.5]])
>> array([1.47011206])규제가 있는 모델은 대부분 입력 특성의 스케일에 민감하기 때문에, 데이터의 스케일을 맞춰주는 것이 중요하다.
StandardScaler등을 사용한다.
1.3 Elastic Net
릿지 회귀와 라쏘 회귀를 절충한 모델
- 릿지, 라쏘의 규제항을 더해서 사용
- 혼합 비율 r 로 혼합 비율을 조절 =
l1_ratio
➡ r=0 : 릿지회귀와 같음 / r=1 : 라쏘회귀와 같음
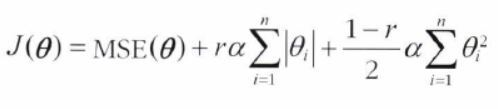
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
>> array([1.54333232])1.4 정리
- 평범한 선형 회귀는 피한다. (약간의 규제가 있는 것이 좋으므로)
- 대체로 릿지가 기본
- 쓰이는 특성이 몇 개 뿐인 것 같다면 라쏘나 엘라스틱넷 (불필요한 특성을 제거하므로)
└ 이때 특성 수가 훈련 샘플 수보다 많거나, 특성 몇 개가 강하게 연관된 경우(다중 공선성 존재) 라쏘보다는 엘라스틱넷
✔ 라쏘는 특성 수가 샘플 수(n)보다 많으면 최대 n개의 특성을 선택
❓❓비용함수 식에서의 n과 다른건지???
1.5 조기종료 Early Stopping
검증 validation error가 최솟값에 도달하면 바로 훈련을 중지시키는 방법
- 경사 하강법과 같은 반복적인 학습 알고리즘을 규제하는 방법
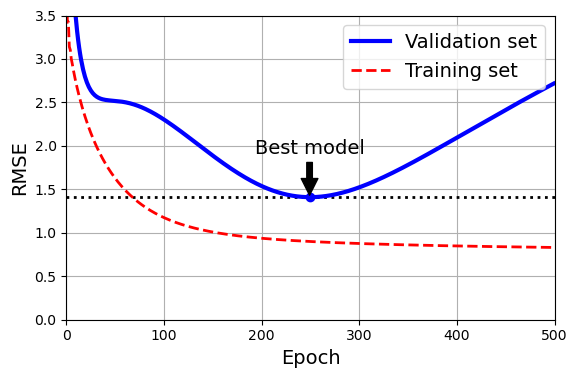
- 에포크 진행 > 훈련 세트에 대한 예측 에러와 검증 에러 감소 (RMSE 감소)
- 검증 에러가 멈추었다가 다시 상승 ➡ overfitting 시작
- 검증 에러가 최소에 도달하는 즉시 멈추는 것이 early stopping
SGD나 미니배치GD에서는 곡선이 매끄럽지 않아 최소값인지 확인하기 어려울 수 있다.
➡ 검증 에러가 일정 시간동안 최솟값보다 클 때 (모델이 더 나아지지 않는다는 확신이 들 때) 학습을 멈추고, 검증 에러가 최소였을 때의 모델 파라미터로 되돌린다.
from copy import deepcopy
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
# 이전과 동일한 2차방정식 데이터셋을 생성하고 분할
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1)
X_train, y_train = X[: m // 2], y[: m // 2, 0]
X_valid, y_valid = X[m // 2 :], y[m // 2 :, 0]
# 전처리 - 90차수의 다항회귀, 편향 포함x, 스케일링
preprocessing = make_pipeline(PolynomialFeatures(degree=90, include_bias=False),
StandardScaler())
X_train_prep = preprocessing.fit_transform(X_train)
X_valid_prep = preprocessing.transform(X_valid)
sgd_reg = SGDRegressor(penalty=None, eta0=0.002, random_state=42)
n_epochs = 500
best_valid_rmse = float('inf')
for epoch in range(n_epochs):
sgd_reg.partial_fit(X_train_prep, y_train)
y_valid_predict = sgd_reg.predict(X_valid_prep)
val_error = mean_squared_error(y_valid, y_valid_predict, squared=False)
if val_error < best_valid_rmse:
best_valid_rmse = val_error
best_model = deepcopy(sgd_reg)partial_fit() : single round of training, 다시 처음부터 시작하지 않고 이전 모델 파라미터에서 훈련을 이어감
2. Logistic Regression
- 샘플이 특정 클래스에 속할 확률을 추정
- 추정 확률이 50%가 넘으면 그 샘플이 해당 클래스에 속한다고 예측
해당 클래스에 속한다 :label=1positive class
속하지 않는다 :label=0negative class
▶ 이진 분류기 Binary classifier
2.1 확률 추정
로지스틱 회귀는 선형 회귀와 동일하게 입력 특성의 가중치 합을 계산하고 편향을 더한다.
그리고 결과에 로지스틱logistic = 시그모이드sigmoid 함수를 적용한다.
- 로지스틱 회귀 모델의 확률 추정
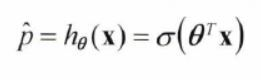
시그모이드sigmoid 함수
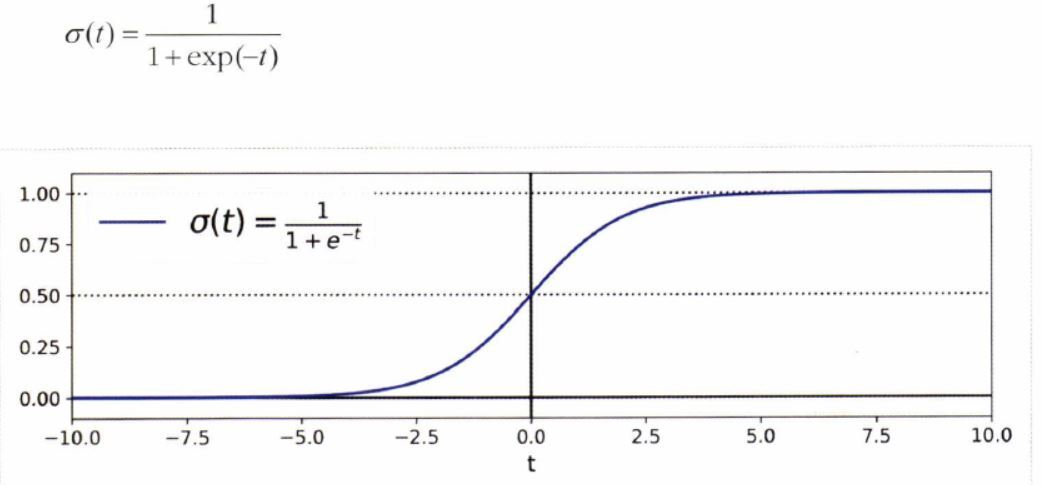
- 0과 1사이의 값을 출력 (S자 형태)
t : 로짓(logit)
: [0,1] 0과 1 사의의 값
- 값이 0.5 미만일때는 class 0(음성), 0.5 이상일때는 class 1(양성)으로 예측
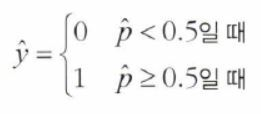
음수 : 0 (음성 클래스)
양수 : 1 (양성 클래스)
2.2 훈련과 비용 함수
- 목표 : y=1(양성 클래스)에 대해 높은 확률 추정, y=0(음성 클래스)에 대해 낮은 확률 추정

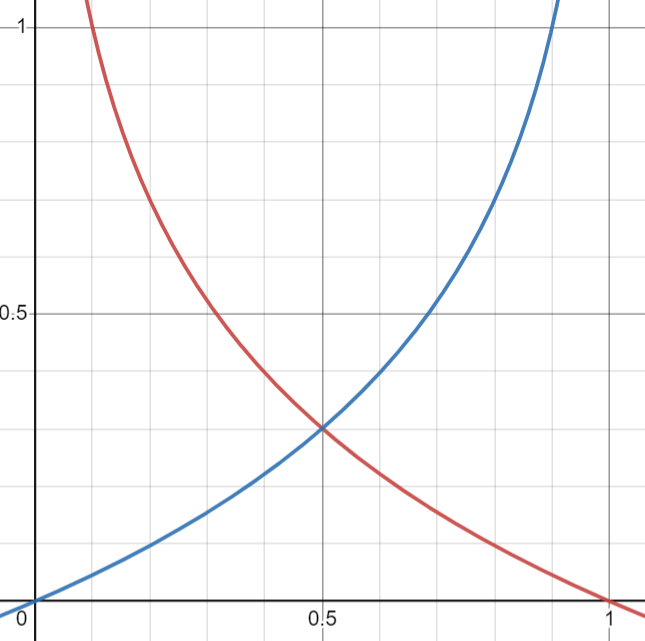
- y=1 : 해당 샘플은 양성이라는 것. (빨간색 그래프)
예측 확률 가 1(양성)에 가까워지면 비용함수가 작아지고
0(음성)에 가까워지면 비용함수가 커진다.- y=0 : 해당 샘플은 음성이라는 것. (파란색 그래프)
예측 확률 가 0(음성)에 가까워지면 비용함수가 작아지고
1(양성)에 가까워지면 비용함수가 커진다.
-
전체 훈련 세트에 대한 비용 함수 (로그 손실log loss)
: 모든 훈련 샘플의 비용을 평균한 것 (샘플 개수 m개)
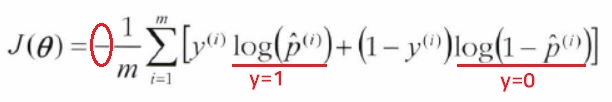
-
비용 함수의 모델 파라미터 를 최소화하는 정규방정식은 알려진 것이 없다.
-
로지스틱 회귀의 비용함수는 볼록함수Convex이다.
따라서 SGD등을 이용하여 전역 최솟값을 찾을 수 있다.
4.3 Decision Boundary
붓꽃iris 데이터셋
샘플 개수 : 150개
품종(3가지) : Setosa, Versicolor, Virginica
특성(4가지) : 꽃잎(petal) 너비와 길이, 꽃받침(sepal) 너비와 길이
Versicolor 종을 감지하는 분류기
1. 데이터 로드 및 확인
from sklearn.datasets import load_iris
iris = load_iris(as_frame=True)
list(iris)
>> ['data','target','frame','target_names','DESCR',
'feature_names','filename','data_module']
iris.data.head(3) # 앞 3개 샘플의 특성
>> sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
iris.target.head(3) # 앞 3개 샘플의 레이블
# 샘플이 섞여 있지 않음
>> 0 0
1 0
2 0
Name: target, dtype: int64
iris.target_names
>> array(['setosa', 'versicolor', 'virginica'], dtype='<U10')- 모델 훈련
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
X = iris.data[["petal width (cm)"]].values # 꽃잎 너비 특성만 사용
y = iris.target_names[iris.target] == 'virginica' # virginica이면 1, 아니면 0
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42) # 랜덤하게 셔플링하고, 데이터 분할
log_reg = LogisticRegression(random_state=42) # 로지스틱회귀 사용
log_reg.fit(X_train, y_train)- 모델의 추정 확률 계산
np.linspace(구간 시작점, 끝점, 구간 내 숫자 개수)
# 꽃잎의 너비가 0~3cm인 꽃에 대해 계산
X_new = np.linspace(0, 3, 1000).reshape(-1, 1) # 열벡터로 크기 변경
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0, 0]
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2,
label="Not Iris virginica proba")
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2,
label="Iris virginica proba")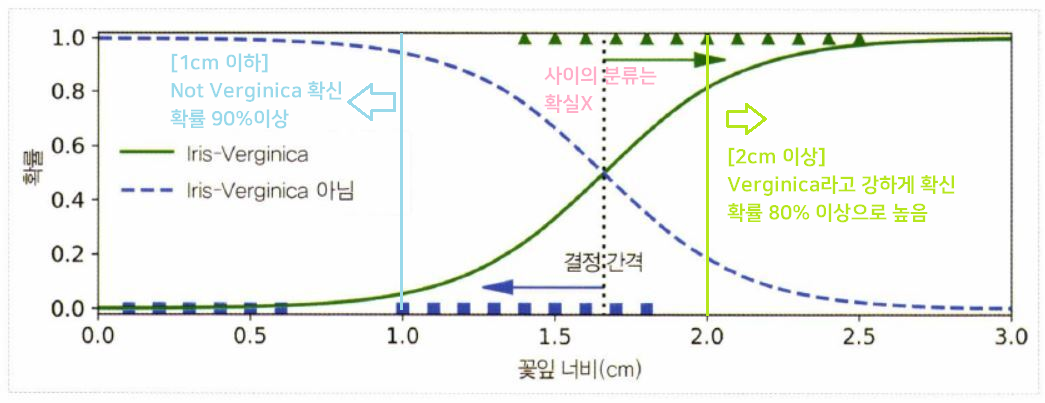
- 1.0과 2.0 사이의 분류는 확실하지 않으나,
predict()method를 사용하면 가장 가능성 높은 클래스를 반환함
✔ 양쪽 확률이 똑같이 50%가 되는 1.6cm 근방에서 결정 경계Decision Boundary 형성
decision_boundary
>> 1.6516516516516517
log_reg.predict([[1.7], [1.5]])
>> array([ True, False])
#1.7cm:Verginica , 1.5cm:not Verginica-
특성 : 꽃잎 너비(petal width)와 꽃잎 길이(petal length)
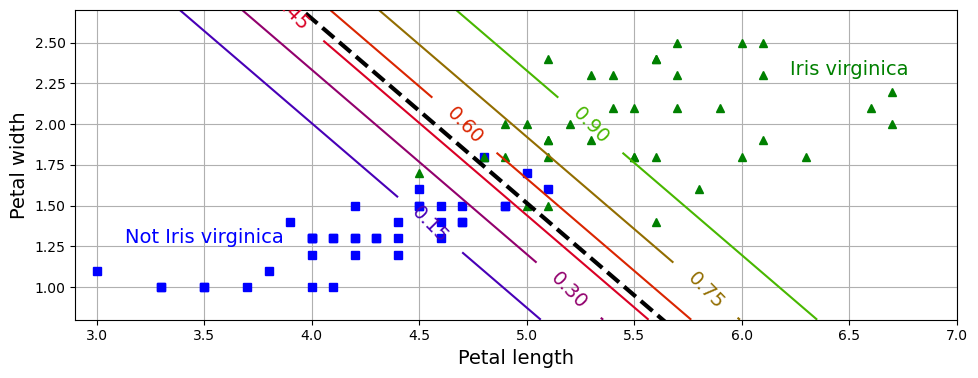
- 점선 : 50% 확률 (0.5) > 결정 경계 Decision Boundary
- 직선들의 숫자 : Verginica라고 판단할 확률
ex. 초록 : 해당 선을 넘어서 있는 꽃들을 90%이상의 확률로 Verginica라고 판단
분류한 클래스를 출력했을 때는 Verginica(1)로 출력될 것이다.
-
로지스틱 회귀 모델도 L1, L2 규제 가능
(사이킷런은 L2가 default)
3. Softmax Regression
로지스틱 회귀 모델을 다중 클래스를 지원하도록 일반화한 것 (=다항 로지스틱 회귀)
✅ 로지스틱 회귀
예측값을 0과 1 사이로 만들고, 두 클래스에 대한 확률의 합은 1
✅ 소프트맥스 회귀
각 클래스마다 확률을 할당 (각 클래스가 정답일 확률), 모든 확률값의 합은 1
위의 빨간색 ? 박스는 소프트맥스 함수이다.
1. 샘플 x에 대해, 각 클래스 k에 대한 점수 를 계산
클래스 k에 대한 소프트맥스 점수
각 클래스는 자신만의 파라미터 벡터 를 가진다.
이 벡터들은 파라미터 벡터 의 행으로 저장된다.
2. 그 점수에 소프트맥스 함수를 적용하여 각 클래스의 확률 추정
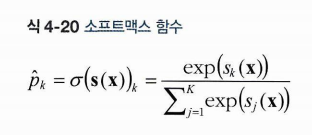
클래스 k일 확률 를 얻는다.
분자 : 클래스 k에 대한 점수를 인풋으로 지수함수 적용
분모 : 모든 지수함수 결과의 합
k개의 클래스에 대한 모든 확률 값을 더하면 1이 된다.
✔ 샘플 x ▶ 클래스 k에 대한 x의 점수 ▶ (소프트맥스 함수) ▶ x가 클래스 k일 확률
3. 추정 확률이 가장 높은 클래스(그냥 가장 높은 점수를 가진 클래스) 선택 (로지스틱 회귀와 동일)
한 번의 하나의 클래스만 예측하므로(출력 클래스는 1개), 상호 배타적인 클래스에서만 사용해야 한다.
cf) 하나의 사진에서 여러 사람의 얼굴을 인식하는 데는 사용 불가
4. 소프트맥스 회귀 훈련 방법
목표 : 타깃 클래스에 높은 확률, 다른 클래스에 낮은 확률
- 크로스 엔트로피cross entropy 비용 함수를 최소화

= 실제값 원-핫 벡터의 i번째 인덱스 (실제 값인 클래스에서 1을 갖고, 나머지에서는 0을 갖는다)일 때 확률 이면 값이 0이 된다. 즉, 최소를 갖게 된다.
타깃 클래스에 대해 1.0으로 예측한 경우가 최소가 되는 식이므로, 해당 식을 최소화하는 방향으로 진행하는 것이다.
m개의 샘플에 대해, 각 샘플마다 k개의 클래스에서 비용함수를 적용하고 이를 m개에 대한 평균을 구한 것이 최종 크로스 엔트로피 비용 함수이다.
-
클래스가 2개인 경우 (k=2) 로지스틱 회귀의 비용함수와 같다.
-
에 대한 그레이디언트 벡터
( 에 대해 미분한 결과이다.)

5. 구현
LogisticRegression : 클래스가 2개 이상일 때 일대다(OvA) 사용
multi_class = "multinomial" : 소프트맥스 회귀 (default:"auto")
solver = "lbfgs" 지정
default로 L2 규제 사용 : 하이퍼파라미터 C ()
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
softmax_reg = LogisticRegression(C=30, random_state=42)
softmax_reg.fit(X_train, y_train)
softmax_reg.predict([[5, 2]]) #꽃잎 길이 5cm, 꽃잎 너비 2cm
>> array([2])
softmax_reg.predict_proba([[5, 2]]).round(2)
>> array([[0. , 0.04, 0.96]]) # 96% 확률로 Virginica(class 2)라고 출력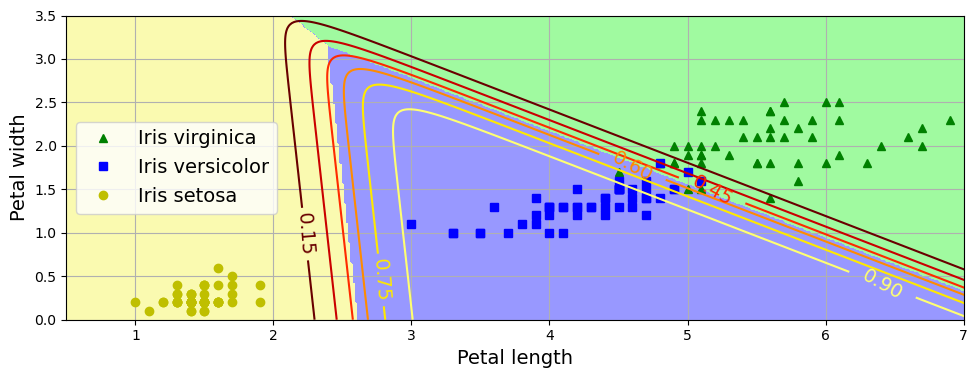
- 클래스 사이의 decision boundary가 모두 선형 (배경색)
- versicolor에 대한 확률 곡선
배치(Batch), 미니배치 학습, 에폭(Epoch), SGD