
1. Gram-Schmidt 직교화 과정
Gram-Schmidt는 서로 직각도 아니고 길이도 제멋대로인 벡터들을 서로 직각인(= 직교) 기준 벡터들로 바꾸는 방법이다.
직교 벡터가 훨씬 계산이 쉽고, 정사영도 정확히 되고 수학적으로 안전한 방식이기 때문이다.


v1 방향으로 비쳐긴 그림자를 빼면 진짜 새로운 방향 v2만 남게 된다.

이걸 계속 반복하면 마지막엔 모든 벡터가 서로 수직인 기준 축이 되고 이것이 바로 직교 기저이다.
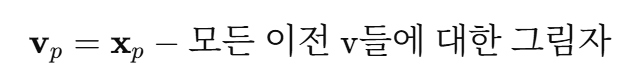
마지막에 모든 벡터의 길이도 1로 바꾸면 정규 직교 기저를 완성할 수 있다.
2. 행렬의 QR 분해
Gram-Schmidt 직교화의 결론을 행렬로 정리한 것이다. 복잡한 행렬 A를 Q(직각 축) x R(얼마나 섞였는지 비율표)로 쪼개는 방식이다.




우리는 Ax = b 문제를 해결하고 싶은데, 역행렬은 어렵고 수가 잘 못되면 구하기 어렵다는 문제가 있다. 그런데 QR 분해를 이용하면 간단하게 풀 수 있다.




3. 최소 제곱법
최소 제곱법(Least-squares Solution)은 선형 방정식 Ax = b가 해를 가지지 않는 불일치한 경우에 최적의 근사해 x를 구하는 방법이다.

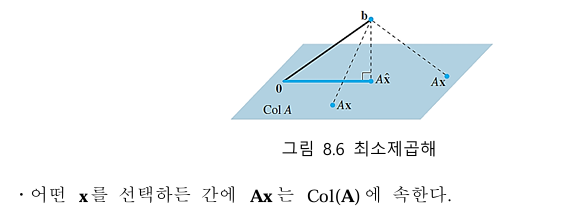
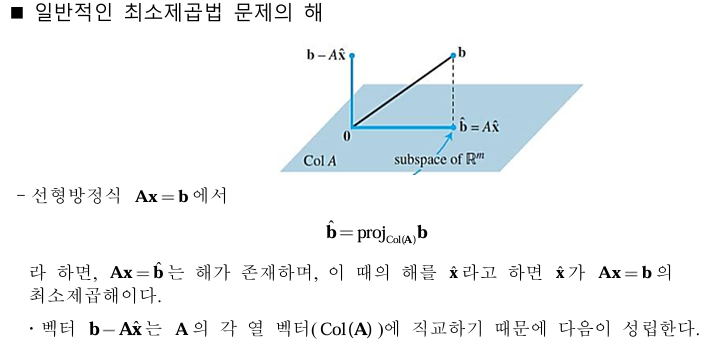


역행렬이 존재하면 딱 하나의 정답이 존재하지만 역행렬이 존재하지 않으면 조건을 만족하는 여러가지 해의 모임이 된다. 즉, 자유 변수가 생긴다는 의미이다.


3-1. 최소 제곱 해의 조건

행렬식이 매우 크거나 매우 작으면 역행렬의 작은 오차가 최소 제곱 해에 큰 오차를 유발할 수 있기 때문에, 행렬 A의 열 벡터 집합이 선형 독립인 경우에 QR 분해를 이용하면 좀 더 신뢰성 있는 해를 구할 수 있다.


원래 공식은 역행렬을 계산하기 어렵기 때문에 QR을 이용하면 정규 직교, 상삼각형으로 인한 역 대입법을 이용해서 풀기가 더 쉬워진다.

