1. 직교 정사영
정사영(Orthogonal Projection)은 벡터를 다른 벡터 방향으로 그림자처럼 내려보낸 것을 말한다. 예를 들어, 우리가 벡터 u와 v 두 개를 갖고 있다고 하자. 그런데 u를 v 방향으로 그림자처럼 내리고 싶다고 하면, 여기서 그 그림자 벡터가 바로 정사영 벡터이다.
정사영 결과는 항상 벡터이기 때문에 정사영과 벡터는 항상 같은 의미가 된다.
2. 직교 기저의 선형 결합
이 부분은 어떤 벡터를 서로 수직인 기준 벡터들을 이용해서 정확하게 표현하는 방법을 설명한다. 어떤 벡터가 주어졌을 때 그걸 직교 기저들을 이용해서 하나의 방법으로만 정확하게 쪼갤 수 있는 것을 보여준다.
3. 부분 공간 위로의 정사영
이번에는 벡터 y를 여러 개의 벡터가 만드는 공간(부분 공간 W) 위로 그림자처럼 내리는 것을 다룬다.
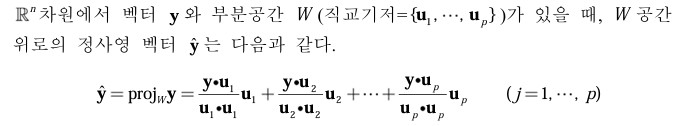
이 정사영은 최대한 가까운 위치로 내려주는 그림자를 말한다.
4. 직교 분해 정리
어떤 벡터 y는 부분 공간 W 위에 내려간 그림자 y 햇과 그 그림자에서부터 y까지 남은 수직 벡터 z이 합으로 나뉠 수 있다.
여기서 y 햇은 W 위에 가장 가까운 위치를 말하고, z는 W에 직각으로 서있는 벡터를 의미한다. 그래서 이걸 직교 분해라고 부른다. 서로 직각으로 나눴기 때문이다.
5. 정규 직교 기저의 정사영
서로 수직이고 길이도 1인 벡터들(= 정규 직교 기저)의 경우에 정사영 계산이 엄청 단순해진다.
그리고 n 차원에서 모든 영이 아닌 부분 공간은 직교 기저 또는 정규 직교 기저를 갖는다.
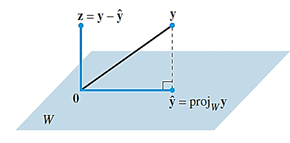
6. 일반 기저와 직교 기저에서의 벡터 x의 표현 방법
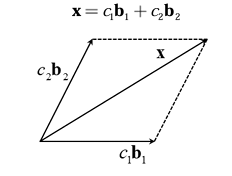
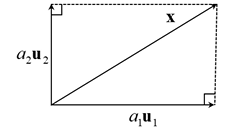
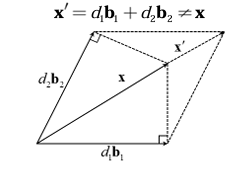
결론적으로 보면 정사영은 직각 방향일 때만 믿을 수가 있다. 일반 기저일 때는 정사영을 사용하면 벡터가 달라질 수 있기 때문이다.
Natural Language Processing and Deep Learning