논문 출처: https://arxiv.org/pdf/1509.02971.pdf

Background

보통 강화학습의 알고리즘을 테스트하기 위해 많이 사용하는 환경 툴이 Gym의 Cartpole-v1이다.

Cartpole에서 Agent는 떨어지지 않기 위해 왼쪽 혹은 오른쪽으로 이동한다. 즉 Cartpole에서 Agent의 정책 밀도함수는 이산적이다. (왼쪽 오른쪽 두 가지 행동에 대한 확률만 정하면 되기 때문이다.)

하지만 행동을 이산적으로밖에 정의할 수 없다면 강화학습을 실생활에 이용하는 것은 불가능하다. 현실은 Action 뿐만 아니라 State 공간 역시도 연속적이기 때문이다. 로봇을 예로 들자. 만약 로봇의 관절을 이동할 수 있는 범위가 있다면 그 범위 이내에는 무한한 행동이 있다. 만약 우리가 지금까지 한 것처럼 Policy Network에 Input을 넣고 각 행동의 확률을 Output으로 반환한다면 이론적으로는 출력 노드의 갯수가 무한개여야 한다. 하지만 이것은 기술적으로 불가능하다. 이것을 해결하기 위해 가장 많이 사용하는 방법은 AGent의 정책 함수 (확률 밀도 함수)를 Gaussian Distribution 이라고 가정하고 Policy는 Gaussian Distribution의 mean과 std를 반환한 후 반환된 mean과 std를 가지고 Random Sampling 하는 것이다. 이런 방식으로 연속공간에 대해 강화학습 (Actor-Critic 계열이 이런 방식을 많이 사용함)을 적용할 수 있다.

하지만 2016년 구글 DeepMind에서 연속공간(Action 공간)에 적용할 수 있는 획기적인 강화학습 알고리즘인 DDPG를 발표하였는데 특이한 점은 정책이 Stochastic Policy 가 아닌 Deterministic Policy라는 것이고 또한 Exploration을 가하기 위해 $\epsilon-greedy$가 아닌 $Noisy$를 사용하였다.

DDPG

DDPG의 가장 큰 특징은

1. No stochastic Policy

상태에 따른 행동의 확률을 과감히 버렸다. 우리는 지금까지 $\pi_\theta(a_t|s_t)$를 policy라고 정의하고 사용하였는데 이것의 의미는 given $s_t$일 때, a_t의 확률 밀도 함수를 의미한다. Policy-Gradient,A2C,A3C,PPO 모두 확률에 기반을 둔 Policy를 사용하였지만 DDPG는 그것을 과감히 버렸다. 이런 Policy를 Deterministic Policy라고 부르고 보통 $a_t=\mu(s_t|\theta)$로 많이 표현한다. ($\theta$라는 parameters로 정의된 신경망 함수)

그런데 만약 상황에 따른 행동이 딱 하나만 있다면 강화학습에서 가장 중요한 Exploration이 제대로 이루어지지 않을 수 있지 않는가. 이것을 해결하기 위해 DDPG는 Noisy를 사용한다.

2. Noisy for Exploration

행동에 Noisy를 넣는다고? 이것이 가능한 이유는 action이 연속값이기 때문이다. 수식으로는 $\mu`(s_t)=\mu_\theta(s_t)+N$ 로 표현하며 N은 보통 Instantly Uncorrelated한 잡음을 선택한다. (강화학습의 고질적인 Correlation 문제를 해결하기 위함)

3. Correlation

DDPG는 Correlation을 해결하기 위해 학습 데이터를 Replay Buffer에 저장하고 일정 시간이 흐른 후 무작위로 뽑아 신경망 학습을 진행한다. 그러면 수식으로 과거 데이터를 사용해서 학습해도 문제가 없다는 걸 수식으로 보여주기만 하면 된다.

강화학습의 목표는 Accumulated Reward를 Maximizing 하는 것이다. 하지만 MDP 가 Stochastic하기 때문에 Expectation of Accumulated Reward를 Maximizing하는 것으로 문제가 바뀐다. 이때 Expectation of Accumulated Reward를 Value function이라고 하며 우리의 목표는 Value 함수를 최대화 하는것이다.

목적 함수를
$J(\theta)=\int\limits_{s_0:a_T}\sum\limits_{k=0}^T \gamma^k r_k P_\theta(s_0:a_T)d(s_0:a_T)$ (목적 함수는 Value function이다 이 식은 Return의 Expectation 적분 식이다.)
$J(\theta)=\int\limits_{s_0}p(s_0)\int\limits_{a_0:a_T} \sum\limits_{k=0}^T\gamma^kr_kp_\theta(a_0:a_T|s_0)d(a_0:a_T)d(s_0)$
$J(\theta)=\int\limits_{s_0}p(s_0) V^{\pi_\theta}(s_0)d(s_0)$

Bellman Equation 에 의해

$V^{\pi_\theta}(s_0)=\sum\limits_{a \in A} \pi(a|s_0) Q^{\pi_\theta}(s_0,a)$ (determinstic이므로 하나만 정해진다)
$V^{\pi_\theta}(s_0)=Q^{\pi_\theta}(s_0,\pi_\theta(s_0))$

$Q^{\pi_\theta}(s_0,\pi_\theta(s_0))=r(s_0,\pi_\theta(s_0))+\gamma\sum\limits_{s` \in S}P_{ss`}^a V^{\pi_\theta}(s`)$

Replay Buffer에서 마음대로 사용하기 위해서는 적분식 안에 확률 밀도함수가 정책 네트워크 parameter $\theta$로 정의되지 않아야 한다.

$V^{\pi_\theta}(s_0)=r(s_0,\pi_\theta(s_0))+\gamma\int\limits_{s_1} V^{\pi_\theta}(s_1)p(s_1|s_0,a_0)ds_1$
$\triangledown_{\theta}V^{\pi_\theta}(s_0)=\triangledown_\theta\pi_\theta(s_0)\triangledown_{a_0}r(s_0,a_0)+\gamma\int\limits_{s_1}\triangledown_{\theta}V^{\pi_\theta}(s_1)p(s_1|s_0,a_0)ds_1+\gamma\triangledown_{\theta}\pi_\theta(s_0)\int\limits_{s_1}V^{\pi_\theta}(s_1)\triangledown_{a_0}p(s_1|s_0,a_0)ds_1$
$\triangledown_\theta V^{\pi_\theta}(s_0)=\triangledown_\theta\pi_\theta(s_0)\triangledown_{a_0}Q^{\pi_\theta}(s_0,a_0)+\gamma\int\limits_{s_1}\triangledown_{\theta}V^{\pi_\theta}(s_1)p(s_1|s_0,a_0)ds_1$
$\triangledown_\theta V^{\pi_\theta}(s_0)=\triangledown_\theta Q^{\pi_\theta}(s_0,a_0)+\gamma\int\limits_{s_1}p(s_1|s_0,a_0)\triangledown_{\theta}V^{\pi_\theta}(s_1)ds_1$
$\triangledown_\theta V^{\pi_\theta}(s_0)=\triangledown_\theta Q^{\pi_\theta}(s_0,a_0)+\gamma\int\limits_{s_1}p(s_1|s_0,a_0)(\triangledown_\theta Q^{\pi_\theta}(s_1,a_1)+\gamma\int\limits_{s_2}\triangledown_\theta V^{\pi_\theta}(s_2)p(s_2|s_1,a_1)ds_2)ds_1$
$\triangledown_\theta V^{\pi_\theta}(s_0)=\triangledown_\theta Q^{\pi_\theta}(s_0,a_0)+ \gamma\int\limits_{s_1}p(s_1|s_0,a_0)\triangledown_\theta Q^{\pi_\theta}(s_1,a_1)ds_1+\gamma^2\int\limits_{s_1,s_2}p(s_2|s_1,a_1)p(s_1|s_0,a_0)\triangledown_\theta V^{\pi_\theta}(s_2)ds_2ds_1$

식의 형태가 재귀적이므로

$\triangledown_\theta J(\theta)=\int\limits_{s_0}p(s_0)\triangledown_\theta V^{\pi_\theta}(s_0)ds_0$
$\triangledown_\theta J(\theta)=\int_{s_0}p(s_0)\triangledown_\theta Q^{\pi_\theta}(s_0,a_0)ds_0+\gamma\int\limits_{s_0,s_1}p(s_0)p(s_1|s_0,a_0)\triangledown_\theta Q^{\pi_\theta}(s_1,a_1)ds_1ds_0+\gamma^2\int\limits_{s_0,s_1,s_2}p(s_0)p(s_1|s_0,a_0)p(s_2|s_1,a_1)\triangledown_\theta Q^{\pi_\theta}(s_2,a_2)ds_2ds_1ds_0+...$
($\gamma$는 수식 전개에서 제거된다.)
$\triangledown_\theta J(\theta)=\sum\limits_{t=0}^T\int\limits_{\zeta}p(\zeta)\triangledown_\theta Q^{\pi_\theta}(s_t,a_t)d\zeta$
결과적으로 적분식에서 확률 밀도함수가 $\theta$에서 자유롭기 때문에 Replay Buffer에서 마음대로 뽑아 사용할 수 있다.

우리의 목적함수는 가치함수다 즉 우리는 목적함수를 최대화해야 한다. 이럴 때 Gradient Ascent방식을 통해 신경망을 업데이트 하는데 목적함수의 Gradient를 그대로 더하면 된다.

우리가 구한 DDPG 가치함수의 Gradient는 Q에 대한 Gradient의 Expectation이다. 현실 적으로 확률 밀도함수를 구하는 것은 어렵기 때문에 Q에 대한 Gradient값을 모아서 평균을 취해서 사용한다. (이것을 Monte Carlo방식이라고 한다.)

$\theta:=\theta+\frac{\alpha}{N}\sum\limits_{i}^N \triangledown_\theta Q^{\pi_\theta}(s_i,a_i)$(N is Batch Size)

4. Target Network

DDPG는 최적 행동 가치 함수 $Q^*$를 찾는 DQN 계열이면서 (DQN 계열은 Replay Buffer를 사용할 수 있다.) Actor와 Critic 2개의 네트워크로 구성된 Actor-Critic 알고리즘다.

Actor는 목적함수(가치함수) 를 최대화 하는 것이 목표고 Critic은 최적 가치함수를 찾는 것이 목적이다. 그러므로 Actor는 Gradient Ascent 방식으로 학습이 진행되고 Critic은 Temporal Difference 을 MSE로 한 Gradient Descent 방식으로 학습이 진행된다. 이때 Actor의 Gradient의 크기를 Critic의 Temporal Difference의 크기가 결정하기 때문에 Critic의 학습이 종료되면 Actor의 학습이 종료된다.

이것을 다시 정리하면

Critic 의 MSE가 0가 되면서 Critic은 최적 가치 함수를 찾았다 -> Actor의 Gradient 크기가 0이 되면서 Actor의 학습이 종료된다. -> 이때 Actor는 최적 가치 함수를 만들었기 때문에 최적 정책을 찾았다.

강화학습은 최적 가치함수를 만드는 최적 정책을 찾는 과정이다.

아가 Critic은 최적 가치함수를 찾는다고 했다. 그렇다면

$\frac{1} {2}(Q^*-Q)^2$가 0에 수렴해야 한다. 하지만 최적 가치함수를 찾는데 최적 가치함수를 어떻게 정의할 수 있겠는가? 그래서 Bellman 방정식으로 근사시키는데 이러한 방식을 Temporal-Difference 시간차 방법이라고 부르고. $r_t+\gamma Q(s_{t+1},a_{t+1})$를 TD-Target이라고 부른다

$\frac{1} {2}(r_t+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t))^2$로 정의할 수 있다. 하지만 TD-Target이 Q 신경망으로 정의 되었기 때문에 Q가 학습된다면 Target 역시 흔들린다. 이것은 학습을 불안정하게 만들어 최적 가치 함수를 찾는 것을 어렵게 만든다. 또한 초기 학습때 OverEstimation Bias 문제를 불러 일으킨다.

그래서 DDPG는 Target-Q Network Target-Actor를 따로 구성한다.

마무리

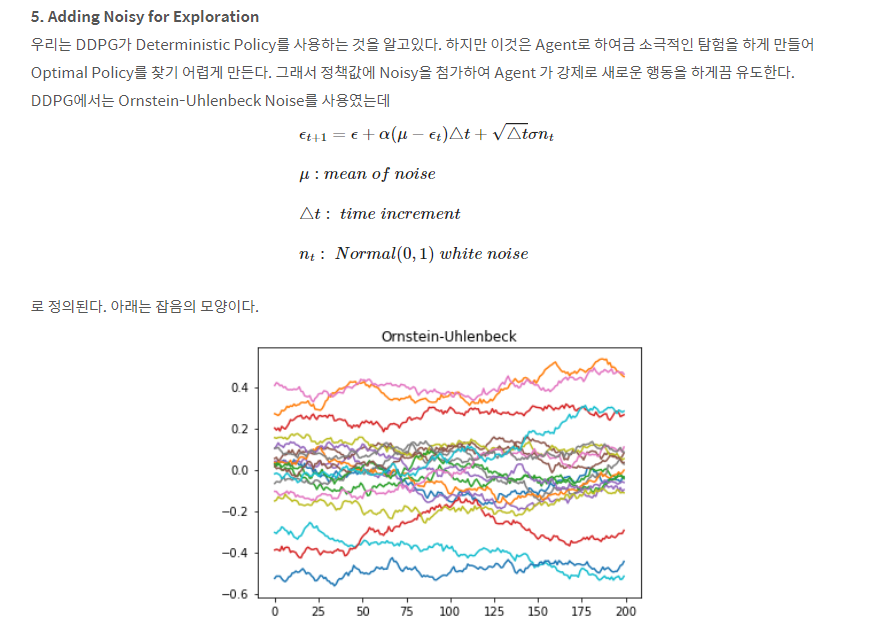
우리는 연속 공간에서 강화학습을 적용하기 위해 만들어진 DDPG에 대하여 알아보았다. 원래 강화학습의 Policy는 기본적으로 Stochastic으로 정의되지만 DDPG는 Deterministic Policy로 어떤 상태에 대해 단 하나의 행동을 고정하였다. 하지만 이렇게 된다면 Agent는 새로운 시도를 하는 것에 소극적이게 되는데 이를 해결하기 위해 잡음을 첨가하였다. 잡음을 첨가해도 되는 이유는 연속 공간에서 행동은
$a \in R$
이기 때문이다. 또한 DDPG는 이전에 PPO 처럼 이전 데이터(학습에 이미 사용한 데이터)를 사용할 수 있으며 학습한 데이터를 바로 사용하는 것이 아니라 Replay Buffer에 담은 후 일정 시간이 흐른 후 무작위로 샘플을 추출해 학습한다. 이런 방식으로 강화학습의 고질적인 문제인 데이터간에 Correlation을 완화 하였다. 마지막으로 A2C A3C PPO 모두 학습이 불안정하게 진행되는데 (Target까지 Critic의 parameter로 정의되어 Critic의 parameter가 update 되면 Target까지 바뀌어 매두 불안정해진다. 달리기를 하는데 골인 지점이 계속 바뀐다고 생각해보라). 이것을 막기 위해 기존 Q-network (critic)과 Actor 신경망을 복사한 Target Q-network Target Actor를 만들고 이들의 parameter updating을 매우 느리게 만듦으로써 이 문제를 해결하였다.

DDPG는 이전 알고리즘과 달리 매우 독특하게 접근한 알고리즘이었다. 긴글 읽어 주셔서 감사하고 글을 여기서 마치겠다.