목적

full column matrix가 있다고 가정하자.
예를 들어 10X3이라고 하자

Ax의 의미가 기하학적으로 A의 column vector들로 span한 Vector space라고 배웠다.

그렇다면 Ax=b의 의미는 Ax라는 subspace에 b가 있느냐 라고 묻는 문제로 재정의할 수 있다.

A[10X3]은 10차원 공간에 있는 3개의 vector로 만든 vector space이다.

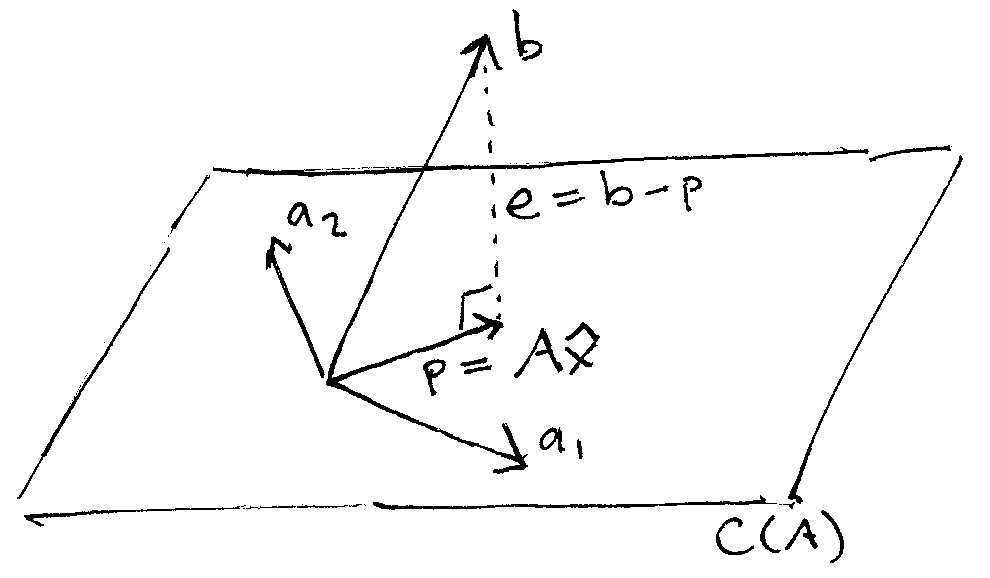
그림은 인간은 3차원밖에 이해할 수 없기 때문에 3차원 공간에 있는 2차원스럽게 이해해보자.

그런데 10차원 공간이라면 A가 만들 수 있는 벡터 공간위에 없을 수도 있다. 위 그림으로 이해하면 C(A) 평면 저 너머에 b가 있는 것이다.

우리는 A를 가지고는 b를 정확하게 표현할 수 없다. 우리가 가진 차원은 3차원이지만 실제 데이터는 10차원에 존재하기 때문이다.

그러면 아예 포기하냐? ㄴㄴ 최소자승법의 목적은 우리가 가진 공간으로 저 b를 최대한 가깝게 표현하자는 것이다. 이것이 바로 최소자승법의 원리이다.

c(A)에 에 나타낼수 있는 모든 벡터중에 b를 가장 잘 대변할 수 있는 벡터는 무엇일까? 바로 C(A)위로 정사영한 벡터이다.

그러므로 최소 자승법과 projection Matrix는 정사영 개념을 이용해 유도한다.

유도

어떤 점과 평면의 거리는 그 점에서 평면에 수직으로 내린 선분의 길이로 구한다.

C(A)의 임의의 벡터 $A\hat{x}$가 있다 가정하자.

$b$와 $A\hat{x}$의 뺄셈으로 vector $e$를 정의할 수 있다.
$e=b-A\hat{x}$
최소자승법은 $\parallel e \parallel_2^2$의 최소화 하는 것이 목표이다.
우리가 찾는 것은 평면 위에 수직으로 내린 선분이므로 (그래야 최소이므로)
$(b-A\hat{x})^TA\hat{x}=0$ 으로 전개할 수 있고 이를 유도하면

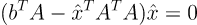
이다. 그런데 우리는 $\hat{x}=0$인 trivial한 해를 구하는 것이 아니기 때문에

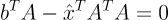
을 풀어야 한다.
식을 전개하고 양변에 transpose를 취한다.

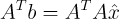
이때 $A^TA$를 Projection Matrix라고 부른다

우리가 아까 full-column rank라고 가정했고 $A^TA$는 (3X3) matrix이므로 $A^TA$는 역행렬이 존재한다. ($rank(A^TA)=rank(A)$ 증명은 Appendix 참고)

$\hat{x}=(A^TA)^{-1}A^Tb$ $\hat{x}$는 vector space에서 임의의 vector을 만들기 위한 coefficient를 묶은 것이다.

그러므로 벡터 b를 col(A)에 정사영한 vector는 $A\hat{x}$이다.

정리

• Projection Matrix: $A^TA$
• $e=A\hat{x}=A(A^TA)^{-1}A^Tb$

만약 A가 coulumn full rank가 아니라면 Pseudo inverse를 구해서 전개한다.

활용

신호처리 관점에서의 이해

신호처리 뿐만 아니라 과학에서 제일 중요한 것은 함수찾기다..

즉 x라는 input과 y라는 output이 있을 때 Ax=y 일때 대응관계 A를 찾는 것이다(A를 법칙이라고도 부를 수 있다.)

그런데 신호처리를 공부하면 알고 있겠지만 신호에는 잡음이 끼게 된다.

$Z=Ax+n$ 이때 $Z$를 $measurement$라고 부른다.

우리는 Z를 보고 x를 구할 수 있어야 하는데 noise n때문에 정확하게 표현할 수 없다. 이때 최소자승법을 col(A) 공간 위로의 정사영을 계산해 근사한다.

포물선 근사

관측된 데이터 $(x_1,y_1),(x_2,y_2)...$를 포물선 $f(x)=ax^2+bx+c$로 근사할 경우에는 다음과 같은 식을 세울 수 있다.

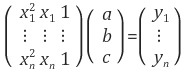
포물선 이상의 3차, 4차, ... n차 함수로 근사할 경우에도 마찬가지이다. 이와 같이 식을 세운 후 matlab 등의 툴로 pseudo inverse 계산을 해 주면 바로 답을 얻을 수 있다.

한계

최소자승법은 데이터 중에 보통 outlier(정상적인 데이터 분포에서 동떨어진 데이터)라고 불리는 이상한 놈이 하나라도 끼어 있으면 적용하기 힘든 방법이다.

그 이유는 최소자승법은 전체 데이터의 $\parallel e \parallel_2^2$ 합을 최소화하기 때문에 outlier의 residual도 같이 줄이려고 하다보면 전혀 엉뚱한(잘못된) 근사 결과를 낼 수 있기 때문이다. 따라서, outlier가 존재하는 경우에는 RANSAC, LMedS, M-estimator 등과 같은 robust한 파라미터 추정 방법을 사용해야 한다.

Appendix

$rank(A^TA)=rank(A)$ 증명

Let $x \in N(A)$ where N(A) is the null space of A and x is $m\times n$ matrix

so,
$Ax=0$
$A^TAx=0$
$x \in N(A^TA)$

Hence $N(A) \subseteq N(A^TA)$

Let $x \in N(A^TA)$
$A^TAx=0$
$x^TA^TAx=0$
$(Ax)^T(Ax)=0$ (this is inner product notation)
$Ax=0$
$x \in N(A)$

Hence $N(A^TA) \subseteq N(A)$

Therefore
$N(A^TA)=N(A)$
$rank(A)=n-N(A)$
$rank(A^TA)=n-N(A^TA)=n-N(A)$
$rank(A^TA)=rank(A)$

참고

https://www.youtube.com/watch?v=B_WZdmCGqBc
https://darkpgmr.tistory.com/56