역행렬 정의부터 시작하자

$AB=I,BA=I$ 일때 B를 A의 역행렬이라고 하고
$B=A^{-1}$로 표기한다.

왜 역행렬이 중요할까? 다시 돌아가자 우리는 선형대수를 공부하는 것은 연립일차방정식을 풀기 위함이다.

다음과 같은 연립일차 방정식이 있다고 가정하자.

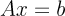
만약 A의 역행렬이 존재하고 우리가 그것을 계산할 수 있다면

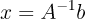
x를 구할 수 있다. 더 중요한 것은 역행렬이 존재한다면 Ax=b의 해는 오직 하나이다

왜냐고? 우리는 행렬을 input vector를 다른 vector로 mapping하는 함수로 바라볼 수 있다. 그러면 역행렬이 있다는 것은 역함수가 존재하는 것이다. 그러므로 역행렬이 존재한다면 연립일차방정식의 해는 유일하다.

역행렬 계산

역행렬 계산은 우리가 이전 시간에 다뤘던 가우스-조던 소거법으로 해결할 수 있다 대표적인 2X2 matrix의 역행렬을 계산해보자. (나머지도 똑같은 원리)

그 전에

AB라는 행렬곱을 두 연립 일차 방정식을 동시에 나타낸다는 아이디어를 받아들여보자.

다음 2개의 연립 일차 방정식이 있다.

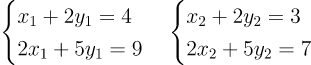
이 2개의 연립 일차 방정식을 한번에 표현할 수 없을까? 가능하다

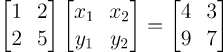
자 이처럼 AB라는 행렬곱을 두 연립 일차 방정식을 동시에 나타낸것이라고 이해할 수도 있다.

역행렬의 정의는

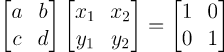
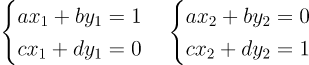
이고 위 사실을 이해하면 역행렬을 계산하는 것은 그저 2개의 연립방정식을 가우스-조던 소거법으로 푸는 과정일 뿐이다!!! 해로 나온 x_1,y_1,x_2,y_2가 을 묶은 행렬이 역행렬인 것이다.

이것을 확장행렬로 표현하면

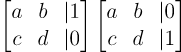
이 된다. 어차피 2개다 목표는 국경선 왼쪽 행렬을 대각행렬로 만드는 것이기 때문에 어른쪽을 한번에 묶어도 상관 없다!! 그러면 다음과 같이 확장행렬을 정의할 수 있다.

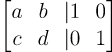
이 확장행렬을 푸는 것이 역행렬을 푸는 과정이다.

계산

의 역행렬을 구하기 위해 확장행렬로 정의하자

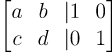
가우스 조던 소거법을 통해 선 왼쪽 행렬을 대각 행렬로 만들면

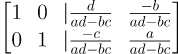
2X2 행렬의 역행렬은

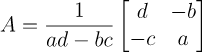
이다.

그런데 ad-bc=0이면 분모가 0이기 때문에 역행렬 없잖아?

(눈이 매섭다) 맞다. 역행렬을 계산하기 전에 ad-bc를 계산해서 역행렬이 있는지 없는지 확인할 수 있다. 이것을 그 유명한 행렬식(determinant)라고 부른다.

우리는 행렬식을 계산함으로써 행렬에 역행렬이 존재하는지 판별할 수 있다.

역행렬의 성질

역행렬을 가진 행렬은 다음의 조건을 만족한다.
아 그전에 역행렬이 있는 행렬을 non singular matrix라고도 부른다. 반대로 역행렬이 없다면 singular matrix(이 단어는 나중에 SVM 할때 나오는 단어다)

A 가 역행렬을 가진다는 명제는 다음 명제들과 필요불충분 관계이다.

• $det(A)\neq0$
• A is full rank (정사각 행렬이면서 열벡터 모두 선형독립이다.)
• $N(A)=0$ ($N(A)=n-rank(A)$)

Q 잠만 일단 첫번째는 determinant가 역행렬이 있는지 확인하기 위해서 배운다고 했으니(0이면 분모가 0이라서 역행렬 없었다는 걸로 기억하는데) 머 그러려니 넘길 수 있는데 2,3번째부터 무슨 말인지 모르겠습니다!!

ok 역행렬이 있다는 게 역함수 있다는 것과 같은 말이라고 했지?
그러면 Ax=b라고 했을때 b를 만들 수 있는 x는 오직 하나라는 거야

그렇지?

그런데 full rank라는 게 무슨 말이야? 열벡터들이 모두 선형독립이라고 했잖아. n개의 벡터집합이 선형독립이라면 n차원에 있는 모든 벡터들을 표현할 수 있고 그 표현방법은 오직 하나야 그렇기 때문에 역행렬이 되려면 무조건 full rank여야 하고 그게 아니면 역행렬이 존재할 수 없어.(우리는 Ax=b를 해석할 때 A에 있는 열벡터의 션형결합으로 b를 표현하기 위한 coefficient를 모든 vector을 x라고 배웠다.)

세번째는 아래 식보면 단번에 이해 ㅆㄱㄴ
$N(A)=n-rank(A)$

역행렬의 성질

• $(AB)^{-1}=B^{-1}A^{-1}$
• $(A^{-1})^{-1}=A$
• $(kA^{-1})=\frac{1}{K}A^{-1}$
• $(A^T)^{-1}=(A^{-1})^T$
• $det(A^{-1})=\frac{1}{det(A)}$

Determinant

우리는 Determinant를 배울때 역행렬 있는지 없는지 판별하기 위해서 계산하는 값이 Determinant라고 했다. 0이면 없는거고

일단 Determinant는 정사각행렬에서만 정의한다. (왜냐고? 애초에 정사각행렬이 아니면 저얼대로 역행렬이 존재하지 않거든 https://velog.io/@everyman123/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%EC%9D%98-%EA%B8%B0%EC%B4%88-%EA%B0%9C%EB%85%90%EB%93%A4#axb%EC%9D%98-%ED%95%B4%EC%9D%98-%EC%88%98-%EC%95%8C%EC%95%84%EB%82%B4%EA%B8%B0
Ax=b의 해의 수 알아내기 항목 참고)

3X3 행렬식은 다음과 같이 계산한다.

사실 계산은 컴퓨터가 해주니 우리가 가져가야 하는 것은 성질이다. (성질을 알아야 고차원에서 가지고 놀 수 있기 때문 ㅇㅇ)

성질

• $det(A)=0$ 이면 A 는 역행렬이 존재하지 않는다 역도 성립(sigular).
• rank-deficient 이면 A는 역행렬이 존재하지 않는다. 그러므로 $det(A)=0$ 역도 성립(full rank여야 역행렬 존재)
• A가 triangular 또는 diagonal matrix이면 $det(A)$은 대각성분들의 곱이다. $det(A)=\prod\limits_i^n a_{ii}$
• $det(I)=1$
• $det(A^T)=A$
• $det(AB)=det(A)det(B)$
• $det(A^{-1})=\frac{1}{det(A)}$