Insight

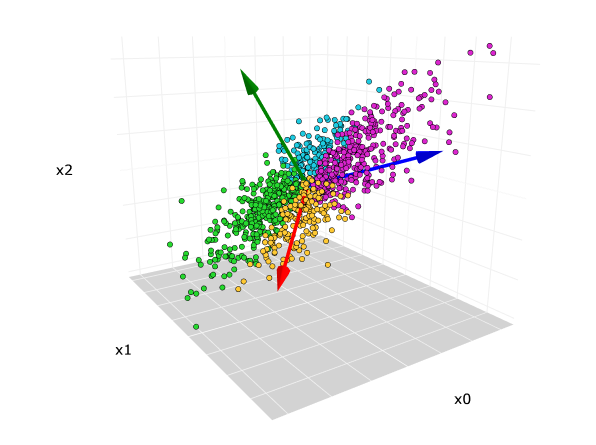
PCA가 차원 축소를 위해 사용한다는 것 정도는 모두가 알고 있을 것이다.

차원을 축소한다는 것은 무슨 의미이지? 저기 3차원 데이터 분포가 있다고 가정하자. 차원을 줄인다것은 저 데이터를 2차원 평면이나 1차원 직선으로 정사영 내린다는 것을 의미한다. 하지만 차원 축소를 한다고 해도 그 데이터 분포의 성질을 최대한 유지해야 하므로 2차원에 정사영하는 것이 옳은 전략이다.

즉 PCA는 정사영을 통해 차원을 축소한다. 하지만 원래 데이터의 성질 (분포) 최대한 보존해야 한다.

PCA를 한글로 풀어쓰면 주성분 분석이다.

PCA를 통해 데이터의 분포를 가장 잘 설명하는 주성분벡터를 찾고 거기로 정사영을 내리면 데이터의 성질을 최대한 보존할 수 있다.

앞으로 복잡한 수식 증명을 통해 주성분을 찾을 것이지만 Insight 챕터는 PCA의 주성분이 무슨 뜻인지 직관적으로 받아들일 것이다.

바로위 사진은 2차원 데이터의 분포를 나타낸다. 만약 어떤 벡터 위에 정사영했을때 저 데이터 분포를 가장 잘 설명하는 vector는 무엇일까?

딱봐도 알겠지만 가장 길쭉하게 분포한 방향으로 정사영을 내리면 저 데이터 분포를 최대한 보존하며 차원 축소를 할 수 있다.

즉 주성분은 데이터 분포에서 가장 분산이 큰 방향이다.

증명

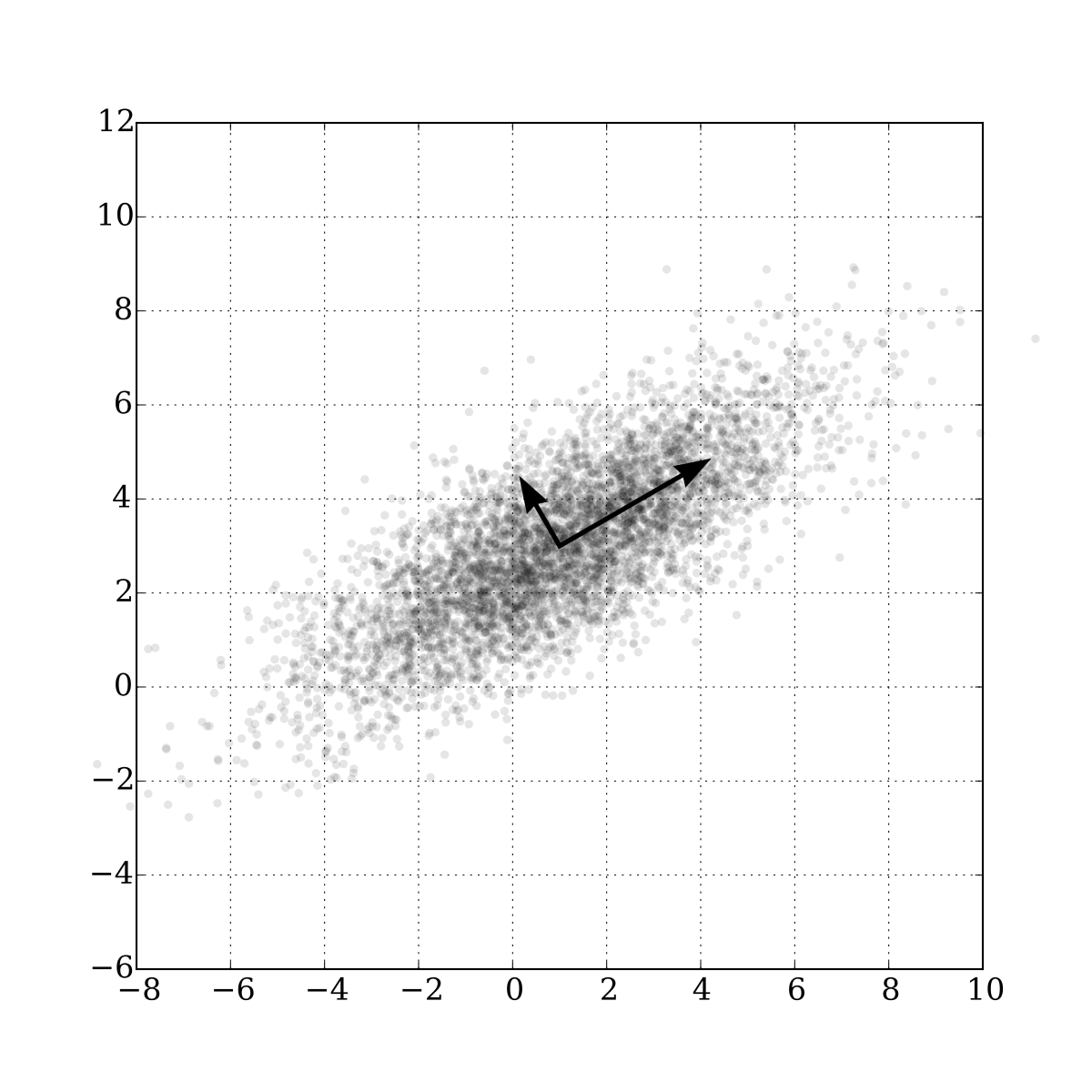
우리가 구하는 것은 성분,벡터이다. 계산상 편의를 위해서 데이터 분포를 원점으로 옮기자.

원점으로 옮기기 위해 데이터분포의 중심을 구하고 빼서 평행이동 시키면 된다. 이걸 수식으로 표현하면

($\tilde{d}$는 원래 데이터의 위치 $\bar{d}$는 데이터의 평균점 $d$는 중심점을 원점으로 평행이동한 후 데이터의 위치)

우리가 찾는 주성분 벡터를 $\mu$라고 정의하자 ($\mu^T\mu=1$)

PCA의 핵심 유도 아이디어는 "데이터를 어떤 벡터 $\mu$로 정사영했을 때 오차가 가장 적은 벡터가 주성분이다."

이를 수식으로 표현하면

우측 식을 가지고 놀아야 한다.

$d_i^Td_i$ 는 고정된 값이기 때문에 식에서 없애도 된다. 식을 정리하면

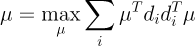
이다.
여기서 $d_id_i^T=(\tilde{d}-\bar{d})(\tilde{d}-\bar{d})^T$인데 이것은 데이터 분포 D의 공분산 행렬이다.

라는 최적화 문제를 풀기 위해 라그랑주 승수법을 사용하자

$R$은 데이터의 공분산 행렬이다. 이 식을 벡터 $\mu$로 나누고 그 결과가 0인 극값이 우리가 찾고자 하는 주성분벡터이다.

(공분산 행렬은 symmetric matrix이다.)

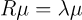
주성분은 공분산 행렬의 고유벡터이다

공분산 행렬은 symmetric matrix이기 때문에 다음과 같이 식을 전개할 수 있다.

$\mu$는 R의 eigenvector 즉 orthonormal matrix이기 때문에

주성분은 공분산 행렬 R의 eigenvalue가 가장큰 eigenvector이다.
그러므로 분산이 가장 큰 방향이 첫번째 주성분이다. 그리고 orthonormal vector이기 때문에 두번째 주성분 첫번째 주성분의 수직인 방향이다.