Insight
우리는 어릴 때 배운 수학지식들을 행렬에 대입하여 이해해왔다.
(행렬곱이 합성함수라느니 역행렬이 역함수라느니 행렬이 함수라느니 등) 말이다.
그런데 행렬에 인수분해도 가능할까? 가능하다. 행렬 또한 다른 행렬들의 곱으로 분해가 가능하다. 고윳값 분해(EVD) 그 유명한 SVD, LU 분해등이 바로 행렬을 분해하는 방법들이다.
그런데 행렬을 분해하는 이유는 무엇일까? 여러가지 이유가 있고 나도 모르는 이유도 있겠지만
일단 선형변환 벡터에 행렬을 곱하는 행위가 기하학적으로 무슨 의미가 있는지 생각해보면 행렬곱의 의미는 벡터를 돌리고 크기를 조절하는 것이다. (여기서 벡터가 회전하지 않고 자신의 방향을 유지하면 그 변환에 대하여 고유벡터이다.)
고윳값 분해는 쉽게 말해
돌리고 늘리고의 과정을
회전 -> scaling -> 회전이라는 3개의 과정을 3개의 행렬로 분해하는 과정이다. 여기서 회전은 eigenvector를 열벡터로 만든 행렬이 scaling은 eigenvalue들을 대각행렬로 만든 행렬이 담당한다.
이런게 어디다 쓰냐고? 다음 시간 PCA를 통해 이것이 어떻게 쓰이는지 알아볼 것이다.그리고 Symmetric matrix의 Eigenvalue decomposition을 통해 행렬에 대한 재밌는 Insight를 얻을 수 있다.
정의
고윳값 분해는 정사각행렬에 대해서만 정의할 수 있다.(eigenvalue,eigenvector를 구하는 게 정사각행렬만 가능하기 때문이다.)
를 행렬이라 가정하고 2개의 eigenvalue 2개의 eigenvector 가 있다고 가정하자.
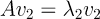
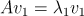
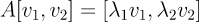
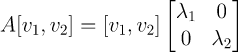
로 정의하자
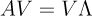
행렬 는 역행렬이 존재한다. 0이 아닌 eigen vector들은 선형독립이고 그러면 정사각 행렬 는 full-rank이기 때문이다.

이때 는 고유값의 대각행렬이고 는 eigenvector을 열벡터로 갖는 행렬이다. A가 정사각행렬인 것처럼 모두 정사각 행렬이다.
Diagonalizable
어떤 정사각 행렬 에 대하여 역행렬이 존재하는 임의의 행렬 V로 다음 연산을 통해 임의의 대각 행렬 를 만들 수 있다면 행렬 를 Diagonalizable하다고 한다.
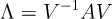
행렬 A가 diagonalizable하기 위해는 A는 열의 갯수만큼의 eigenvector를 가지고 있어야 한다. (서로 다른 고유값들에 대응되는 고유벡터들은 선형독립이다)
왜 이게 중요하냐?

이기 때문이다.
Eigenvalue Decomposition이 가능하면 Diagonalizable 하다는 의미이고 인 행렬이다. 대각행렬의 rank는 non-zero element의 숫자로 결정되기 때문에 Non-zero eigenvalue의 갯수를 통해 행렬 의 rank를 알 수 있다. Eigenvalue Decomposition을 하면서 rank도 덩달아 알 수 있다.
성질
- rank-deficient 인 행렬은 다음 명제와 필요 불충분 관계이다.
- 인 eigenvalue가 적어도 하나 있다.
- 증명 rank-deficient라면 역행렬이 존재할 수 없으므로 이다. 우리는 특이값 분해의 성질을 통해 가 특이값들의 곱이라는 사실을 알고 있다. 라는 말은 0인 특이값이 적어도 하나이상 존재한다는 의미이다.
- 의 eigenvalue와 의 eigenvalue는 같다.
- 증명:
- 가 orthogonal matrix라면 는 1 또는 -1 이다.
or
Symmetric Matrix
인 행렬을 Symmetric Matrix라고 부른다. 대각행렬은 Symmetric Matrix이다.
만약 A가 Symmetric Matrix라면
위 식을 통해
를 유도할 수 있는데 이것은 orthogonal matrix의 조건이다.
보통 orthogonal matrix를 로 정의하기 때문에 식을 다시 정리하자.
이다.
가 Symmetric Matrix라면 특이값 분해가 매우 쉬워진다. 왜냐하면 Orthogonal Matrix의 역행렬은 Transpose를 취하면 되기 때문이다.
그런데 이건 계산을 하면 되는거고 Symmetric Matrix면 행렬에 대한 재밌는 시각을 얻을 수 있다.
Symmetric Matrix 에 대하여 특이값 분해를 하면 다음과 같다. (는 orthogonal matrix의 열벡터인 orthonormal vector이다.)


가 symmetric matrix라면 위와 같이 행렬을 각각의 eigenvector(orthonormal matrix)들로 만든 rank-1 matrix들의 합으로 분해할 수 있다. !! (자신과 자신의 transpose의 곱으로 만들어진 행렬은 rank가 1이다.)
그런데 이게 무슨 의미이지?

선형변환은 함수이다.
를 다르게 위 정의로 나타내면
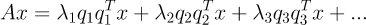
이다.
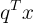
는 벡터 q 위로 x를 정사영했을 때의 scalar값이다.

는 방향으로 (는 orthonormal이라 크기가 1이고 방향만 있는 벡터이다.) 만큼 상수배를 해준다는 것이다.
눈치 빠른 사람은 알겠지만 위 식은
x를 A의 eigenvector의 선형결합으로 표현한 것이다!!!
즉, 가 symmetric matrix라면 를 eigenvector(orthonormal matrix)의 선형결합으로 표현할 수 있다.
참고
Robotics 101: Computational Linear Algebra (https://github.com/michiganrobotics/rob101)
공돌이의 수학정리노트 (https://angeloyeo.github.io/2020/11/19/eigen_decomposition.html#%EA%B3%A0%EC%9C%B3%EA%B0%92-%EB%B6%84%ED%95%B4%EC%9D%98-%EA%B8%B0%ED%95%98%ED%95%99%EC%A0%81-%EC%9D%98%EB%AF%B8)
혁펜하임 선형대수 수업
(https://www.youtube.com/watch?v=xDARfmKauuA&list=PL_iJu012NOxdZDxoGsYidMf2_bERIQaP0&index=20)
