
📌 활성화 함수(Activation Function)
📖 Activation Function 개념
-
신경망은 선형회귀와 달리 한 계층의 신호를 다음 계층으로 그대로 전달하지 않고, 비선형적인 활성화 함수를 거친 후에 전달한다.
-
사람의 신경망의 뉴런들도 모든 자극을 다 다음 뉴런으로 전달하는것은 아니고, 역치 이상의 자극만 전달하게 된다. 활성화 함수는 이런 부분까지 사람과 유사하게 만들어 사람처럼 사고하고 행동하는 인공지능 기술을 실현하기 위해 도입되었다.
-
또한 선형모델을 기반으로 하는 딥러닝 신경망에서 분류 문제를 해결하기 위해서 비선형 활성화 함수가 필요하다.
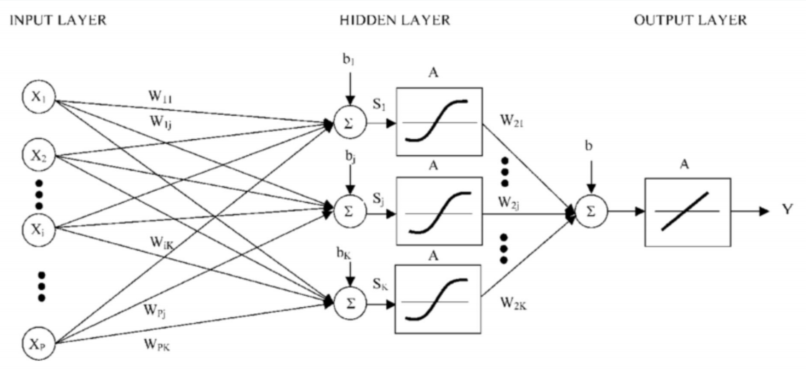
위 사진을 볼 때에 활성화 함수는 층에 따라 다른 활성화 함수를 사용 할 수 있다는 것을 확인 할 수 있다.
📖 활성화 함수 종류
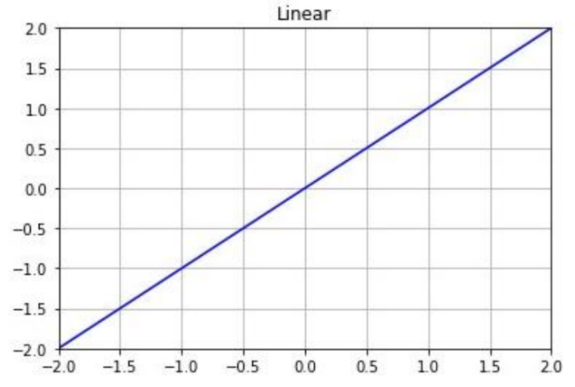
Linear function(선형 함수 = 항등함수) > 회귀
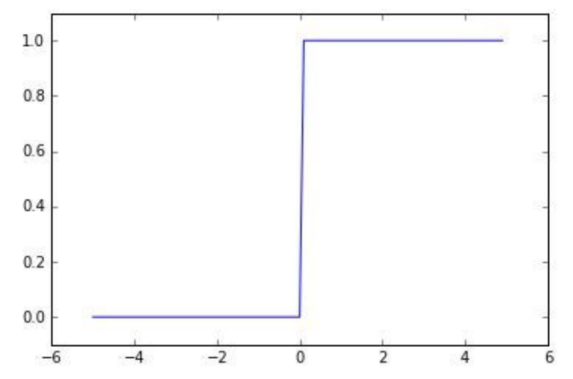
Step function(계단 함수) > 분류의 초기 활성화 함수
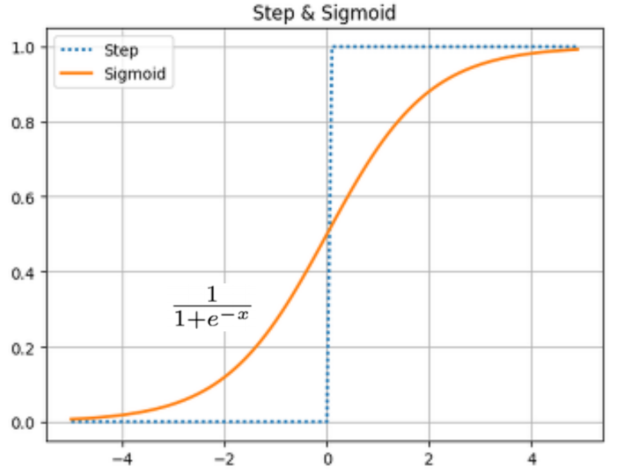
Sigmoid 함수 > 이진분류
📖 활성화 함수 정리
📋 중간층에서 활성화 함수로 비선형 함수를 사용하는 이유
- 계단 함수(step)과 시그모이드 함수(sigmoid)는 비선형 함수이다.
- 활성화 함수로 선형함수(linear)
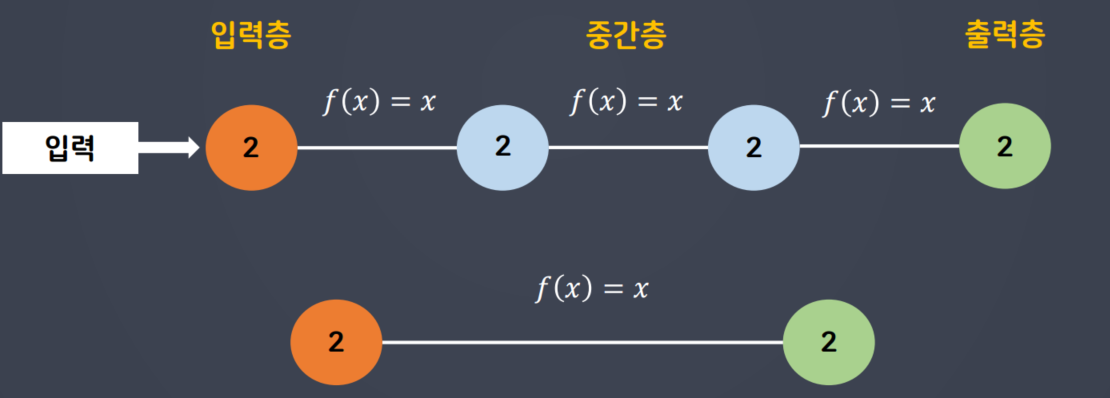
Ex) h(x) = cx를 사용하면 중간층(은닉층)을 여러 개 구성한 효과를 살릴 수 없다.
📋 중간층에서 활성화 함수로 선형함수를 사용하게 된다면
선형함수(linear) 수식은 h(x) = x
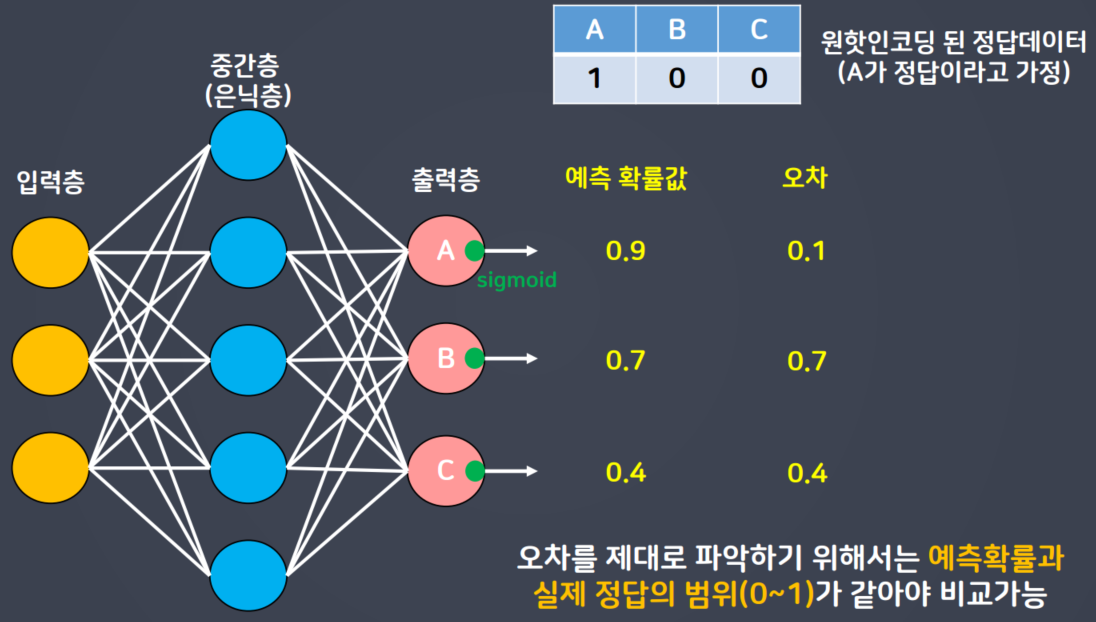
- 딥러닝 신경망에서 다중분류 문제를 해결하는 프로세스는 각 레이블에 대한 확률 값을 토대로 가장 높은 확률 값을 가지는 레이블로 최종 분류를 진행함
- 각 레이블의 확률들을 알기 위해 출력층 퍼셉트론 개수를 레이블 개수와 맟춰야 함(하나의 퍼셉트론이 하나의 레이블에 대한 롹률값을 출력)
- 다중 분류 문제의 경우 정답 데이터를 원-핫 인코딩 해야 함
- 신경망 학습을 위해서는 원-핫 인코딩 된 정보와 출력층의 각 퍼셉트론이 예측한 확률과의 오차를 바탕으로 신경망이 학습하게 됨
📋 소프트맥스(softmax)함수 > 다중분류
다중분류에서 레이블 값에 대한 각 퍼셉트론의 예측 확률의 합을 1로 설정하였을 때에,
sigmoid에 비해 예측 오차의 평균을 줄여주는 효과를 가지고 있다.
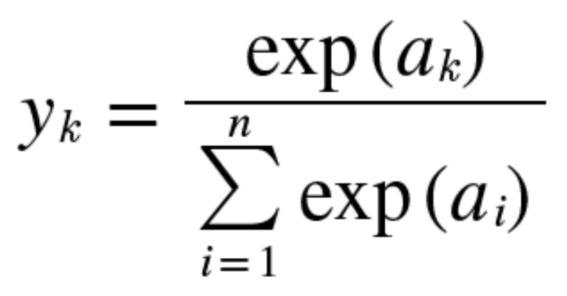
📋 소프트맥스(softmax)함수 코드 구현
import numpy as np
def softmax(x):
e_x = np.exp(x-x.max())
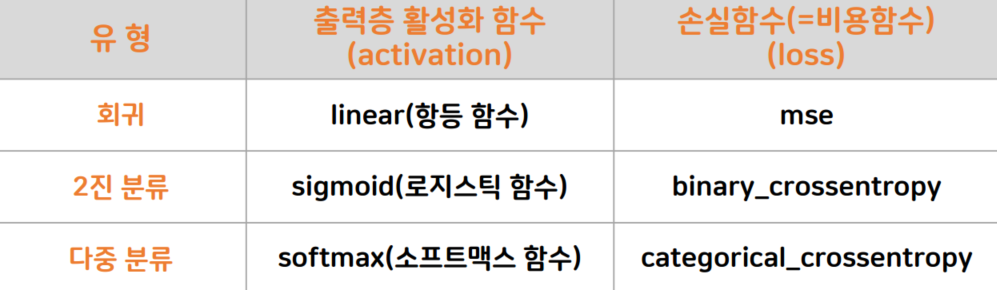
return e_x/e_x.sum()📖 활성화 / 손실함수의 종류
📌 오차 역전파(Back Propagation)
📖 Back Propagation 개념
-
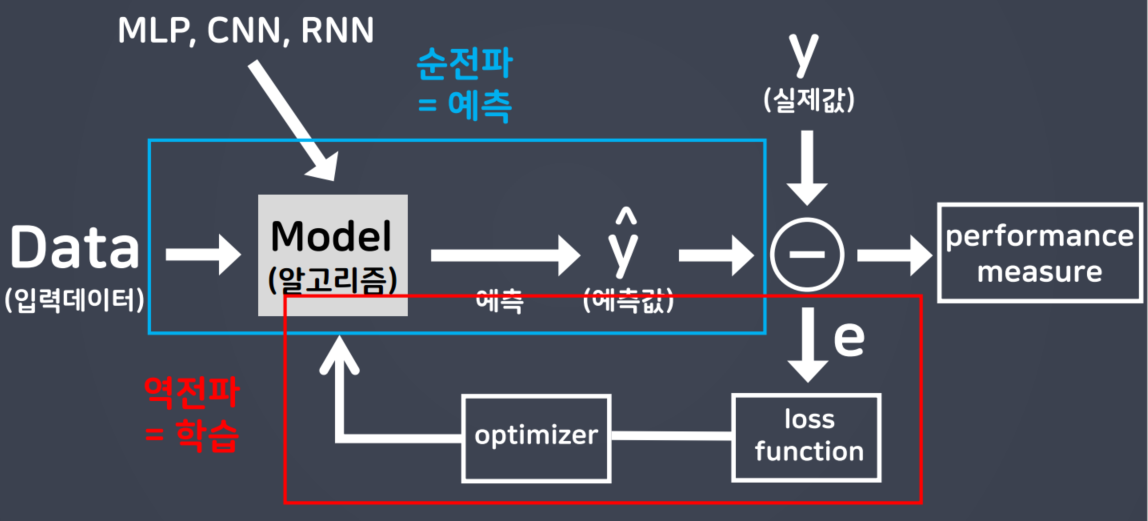
순전파 : 입력 데이터를 입력층에서부터 출력층까지 정방향으로 이동시키며 출력값을 예측해 나가는 과정이다.
-
역전파 : 출력층에서 발생한 에러를 입력층 쪽으로 전파시키면서 최적의 결과를 학습해 나가는 과정이다.
📖 Back Propagation 수학공식
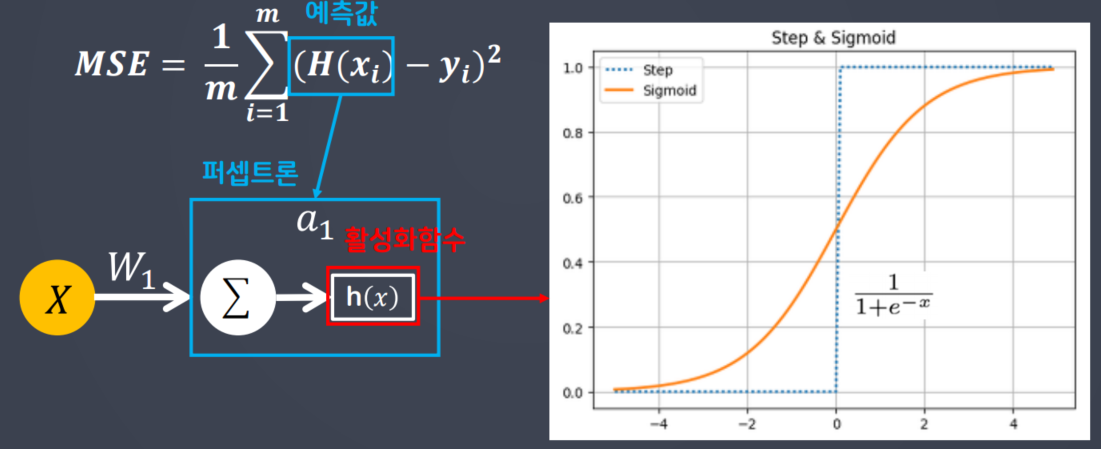
📋 손실함수 및 Sigmoid 함수의 미분
- 선형모델이 학습하기 위해서 경사하강법
(loss 함수를 미분)을 사용 한다.
Sigmoid 함수의 문제점으로 몇가지가 있는데, 대표적으로 기울기 소실 문제(Vanishing Gradient)가 있다.
📌 최적화함수(Optimizer)
📖 Optimizer의 종류
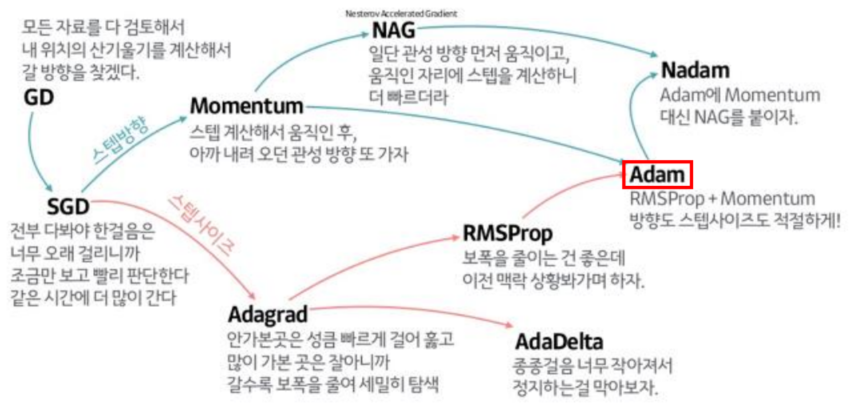
최적화함수(Optimizer)의 종류가 여러가지가 있는데 대표적으로 몇가지만 소개해 보려고 한다.
📋 경사하강법(Gradient Descent Algorithm)
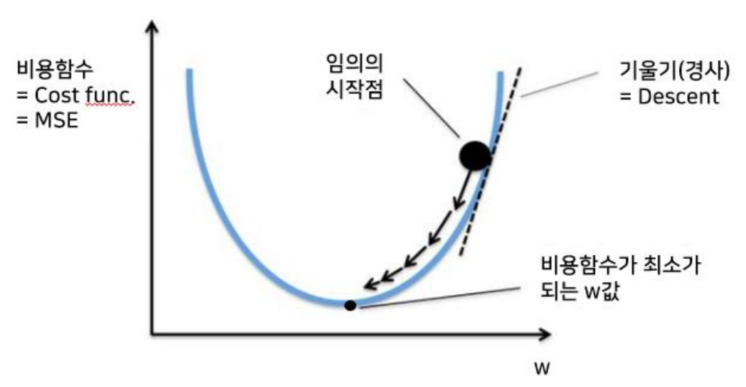
경사하강법은 전체 데이터를 이용해 업데이트를 한다.
비슷한 개념으로는 확률적 경사하강법이 있는데, 확률적으로 선택된 일부 데이터를 이용해 업데이트를 한다. 또 모멘텀은 경사하강법에 관성을 적용해 업데이트 현재 batch뿐만 아니라 이전 batch데이터의 학습 결과도 반영한다.
최적화 함수에 관한 것들은 아래의 사진을 참고하자.
📖 Optimizer 코드
from tensorflow.keras import optimizers
opti = optimizers.SGD(learning_rate=0.01, momentum=0.9)
model.compile(loss='mse', optimizer=opti, metrics=['acc'])📌 마무리
📖 느낀점
여러가지 생소한 모델들이 너무 많아서 어려움이 많이 느꼇다.
생각보다 가장 기본적으로 대중화 (자주 사용하는) 모델들을 주로 외우고 사용할 예정이다.
추후 딥러닝을 계속 공부하고 사용하다보면 자연스럽게 외워질것이라고 생각이 된다.
