서른번째 수업 | 합성곱 신경망 | 전이학습 | Resnet | 암석 식별 머신 구현

강명호 강사님

합성곱 신경망

전체 구조

CNN (Convolution Neural Network)

CNN은 주로 이미지 데이터에서 패턴을 찾아내기 위해 고안된 신경망이다. 사진을 찍으면 인접한 픽셀들이 비슷한 색이나 모양을 가지며 CNN은 이처럼 공간적으로 가까운 데이터들 간의 관게를 학습해 패턴을 알아내는 방식이다.

합성곱 계층

합성곱 연산

import numpy as np

x_input = np.array([[1, 2, 3, 0],
                    [0, 1, 2, 3],
                    [3, 0, 1, 2],
                    [2, 3, 0, 1]])
                    
kernel = np.array([[2, 0, 1],
                   [0, 1, 2],
                   [1, 0, 2]])

# 입력 및 커널 차원
input_height, input_width = x_input.shape
kernel_height, kernel_width = kernel.shape

# 출력 행렬
output_height = input_height - kernel_height + 1
output_width = input_width - kernel_width + 1
output = np.zeros((output_height, output_width))

# 합성곱 연산
for i in range(output_height):
    for j in range(output_width):
        output[i, j] = np.sum(x_input[i:i+kernel_height, j:j+kernel_width] * kernel)

output += 3

print(output)

• 입력 및 커널 설정
  - x_input: 4*4 크기의 입력 행렬.
  • kernel: 3*3 크기의 커널(필터) 행렬.
• 출력 크기 계산
  - 출력 크기는 output_height = input_height - kernel_height + 1과 output_width = input_width - kernel_width + 1로 계산되어 2*2 출력 행렬이 만들어진다.
• 합성곱 연산
  - 중첩된 for 문을 사용하여 커널을 입력 행렬에 슬라이딩하며 각 위치에서 합성곱을 수행한다.
  • np.sum(x_input[i:i+kernel_height, j:j+kernel_width * kernel): 커널과 대응되는 입력 행렬 영역의 값을 곱한 후 모두 더하는 작업.
• 출력에 상수 추가
  - 최종 결과에 3을 더해 출력값을 조정한다.

패딩, 스트라이드 구현

패딩과 스트라이드는 CNN에서 이미지 데이터의 처리를 조절하는 중요한 개념이다.

• 패딩 (Padding): 입력 이미지 주변을 특정 값(주로 0) 으로 채우는 작업.
• 스트라이드 (Stride): 커널이 이동하는 간격

import numpy as np

x_input = np.array([[1, 2, 3, 0, 1, 2, 3],
                    [0, 1, 2, 3, 0, 1, 2],
                    [3, 0, 1, 2, 3, 0, 1],
                    [2, 3, 0, 1, 2, 3, 0],
                    [1, 2, 3, 0, 1, 2, 3],
                    [0, 1, 2, 3, 0, 1, 2],
                    [3, 0, 1, 2, 3, 0, 1]])

kernel = np.array([[2, 0, 1],
                   [0, 1, 2],
                   [1, 0, 2]])
padding = 1
stride = 2

input_height, input_width = x_input.shape
kernel_height, kernel_width = kernel.shape

output_height = (input_height + 2 * padding - kernel_height) // stride + 1 # 스트라이드 고려
output_width = (input_width + 2 * padding - kernel_width) // stride + 1 # 스트라이드 고려
output = np.zeros((output_height, output_width))

padded_input = np.pad(x_input, ((padding, padding), (padding, padding)), mode='constant') # 패딩

# 합성곱 연산 (패딩, 스트라이드 포함)
for i in range(0, input_height - kernel_height + 2 * padding + 1, stride):
    for j in range(0, input_width - kernel_width + 2 * padding + 1, stride):
        output[i // stride, j // stride] = np.sum(padded_input[i:i+kernel_height, j:j+kernel_width] * kernel)

output += 3
print(output)

• 입력 데이터 및 커널 설정
  - x_input: 7*7 크기의 입력 데이터 배열.
  • kernel: 3*3 크기의 커널 배열.
• 출력 크기 계산
  - 패딩과 스트라이드를 고려해 출력의 높이와 너비를 계산.
  $\text{output\_height} = \frac{\text{input\_height} + 2 \times \text{padding} - \text{kernel\_height}}{\text{stride}} + 1$
  • 이 공식에 따라 output_height와 output_width는 모두 4로 설정되며 4*4 크기의 output 배열을 생성.
• 패딩 처리
  - np.pad를 사용하여 입력 행렬 x_input에 위아래 양옆으로 1씩 0을 추가해 패딩된 입력 padded_input을 생성
• 합성곱 연산
  - stride를 고려해 padded_input의 특정 위치마다 커널을 적용하여 합성곱 연산을 수행.
  • stride가 2이므로 i와 j는 각각 2씩 증가하며 커널을 적용.
• 출력 조정
  - 출력 배열 output에 3을 더해 최종 결과를 출력.

풀링 계층 (Pooling Layer)

특징 맵의 크기를 줄이기 위해 사용된다.

Max Pooling

import numpy as np

conved_input = np.array([[1, 1, 2, 4],
                         [5, 6, 7, 8],
                         [3, 2, 1, 0],
                         [1, 2, 3, 4]])
max_pooling_size = 2
max_pooling_stride = 2

input_height, input_width = conved_input.shape
pooling_height, pooling_width = max_pooling_size, max_pooling_size
stride = max_pooling_stride
output_height = ((input_height - pooling_height) // stride) + 1
output_width = ((input_width - pooling_width) // stride) + 1

max_pooling_result = np.zeros((output_height, output_width))  # 풀링 결과 배열

# 풀링 연산
for i in range(output_height):
    for j in range(output_width):
        row_start = i * stride
        row_end = row_start + pooling_height
        col_start = j * stride
        col_end = col_start + pooling_width

        max_pooling_result[i, j] = np.max(conved_input[row_start:row_end, col_start:col_end])
        
print(max_pooling_result)

• 입력 데이터 및 풀링 크기 설정
  - conved_input: 4*4 크기의 입력 배열로 합성곱 레이어를 거친 출력이라고 가정할 수 있따.
  • max_pooling_size, max_pooling_stride: 각각 풀링 영역 크기와 이동 간격을 나타낸다. 여기서는 2*2 크기의 풀링 윈도우를 사용하고 stride가 2로 설정되어 풀링 윈도우가 2칸씩 이동한다.
• 출력 크기 계산
  - 풀링 결과 배열의 크기를 계산하여 2*2 크기의 max_pooling_result 배열을 생성한다.
• 최대 풀링 연산
  - for 루프를 사용하여 conved_input의 각 2*2 영역에서 최대값을 선택하여 max_pooling_result에 저장한다.
  • stride=2이므로 각 2*2 풀링 영역이 겹치지 않고 다음 영역으로 이동한다.

Average Pooling

주어진 풀링 영역에서 최대값을 고르는 Max Pooling과 달리 영역 내 모든 값의 평균을 구해 저장한다.

import numpy as np

conved_input = np.array([[1, 1, 2, 4],
                         [5, 6, 7, 8],
                         [3, 2, 1, 0],
                         [1, 2, 3, 4]])
pooling_size = 2
pooling_stride = 2

input_height, input_width = conved_input.shape
pooling_height, pooling_width = pooling_size, pooling_size
stride = pooling_stride
output_height = ((input_height - pooling_height) // stride) + 1
output_width = ((input_width - pooling_width) // stride) + 1

average_pooling_result = np.zeros((output_height, output_width)) # 풀링 결과 배열

# 풀링 연산
for i in range(output_height):
    for j in range(output_width):
        row_start = i * stride
        row_end = row_start + pooling_height
        col_start = j * stride
        col_end = col_start + pooling_width

        average_pooling_result[i, j] = np.mean(conved_input[row_start:row_end, col_start:col_end])
        
print(average_pooling_result)

• 입력 데이터 및 풀링 크기 설정
  - conved_input: 4*4 크기의 입력 배열.
  • pooling_size, pooling_stride: 풀링 윈도우의 크기와 이동 간격을 나타낸다. 여기서는 2*2 크기의 풀링 윈도우와 stride=2를 설정해 풀링 윈도우가 2칸씩 이동한다.
• 출력 크기 계산
  - 풀링 결과 배열의 높이와 너비를 계산하여 2*2 크기의 average_pooling_result 배열을 생성한다.
• 평균 풀링 연산
  - for 루프를 사용하여 conved_input의 각 2*2 영역에서 평균값을 계산하고 average_pooling_result에 저장한다.
  • stride=2이므로 풀링 영역이 겹치지 않고 다음 위치로 이동하며 계산된다.

합성곱/풀링 계층 구현하기

합성곱 계층 구현

class Convolution:
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b        
        self.stride = stride
        self.pad = pad

    def forward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = int(1 + (H + 2 * self.pad - FH) / self.stride)
        out_w = int(1 + (W + 2 * self.pad - FW) / self.stride)

        col = im2col(x, FH, FW, self.stride, self.pad) # 입력 데이터 전개
        col_W = self.W.reshape(FN, -1).T # 필터 전개
        out = np.dot(col, col_W) + self.b
        
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2) # reshape
        
        return out

• 클래스 초기화(__init__)
  - W: 필터(커널) 행렬. 크기는 (FN, C, FH, FW)이다. 여기서 FN은 필터 개수, C는 채널 수, FH와 FW는 필터의 높이와 너비이다.
  • b: 필터의 바이어스 값. 크기는 (FN,)이다.
  • stride: 필터 이동 간격.
  • pad1: 입력 주변에 추가되는 패딩의 크기.
• 순전파 연산(forward)
  - 입력 크기 및 출력 크기 계산
  - 입력 x의 크기는 (N, C, H, W)이다. N은 배치 크기, C는 채널 수, H와 W는 입력의 높이와 너비이다.
  - 출력 높이(out_h)와 너비(out_w)는 패딩과 스트라이드를 고려해 계산된다.
  $\text{out\_h} = \frac{H + 2 \times \text{pad} - FH}{\text{stride}} + 1$
  $\text{out\_w} = \frac{W + 2 \times \text{pad} - FW}{\text{stride}} + 1$
  • im2col 함수 사용
    • im2col 함수를 이용해 데이터를 펼쳐서 (N * out_h * out_w, C * FH * FW) 크기로 변환한다. 이는 합성곱 연산을 행렬 곱으로 구현할 수 있게 한다.
      • im2col 함수가 필요하고, 이 함수는 입력 데이터의 패치를 펼치는 역할을 한다.
  • 필터 전개
    • 필터 W의 크기를 (FN, C * FH * FW)로 변환하고 전치(.T)하여 (C * FH * FW, FN)크기로 변환한다.
  • 합성곱 연산
    • 펼친 입력 데이터(col)와 필터(col_W) 간의 행렬 곱을 수행하고 바이어스 b를 더해 최종 출력을 얻는다.
  • 출력 형태 변환
    • out은 (N, out_h, out_w, FN) 크기로 변경되고, (N, FN, out_h, out_w)로 다시 전치되어 출력된다.

풀링 계층 구현

class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)

        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad) # 전개
        col = col.reshape(-1, self.pool_h * self.pool_w)

        out = np.max(col, axis=1) # 최대 풀링

        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
        
        return out

• 클래스 초기화(__init__)
  - pool_h, pool_w: 풀링 윈도우(영역)의 높이와 너비.
  • stride: 풀링 윈도우가 이동하는 간격.
  • pad: 입력 주변에 추가되는 패딩의 크기. 일반적으로 패딩은 최대 풀링에서는 거의 사용되지 않지만 설정 가능하도록 추가되었다.
• 순전파 연산(forward)
  - 입력 및 출력 크기 설정**
  - 입력 x의 크기는 (N, C, H, W)이다. N은 배치 크기, C는 채널 수, H와 W는 입력 데이터의 높이와 너비이다.
  - 출력 높이(out_h) 및 너비(out_w)
  $\text{out\_h} = \frac{H - \text{pool\_h}}{\text{stride}} + 1$
  $\text{out\_w} = \frac{W - \text{pool\_w}}{\text{stride}} + 1$
  • im2col 함수 사용
    • im2col 함수를 이용해 입력 데이터를 펼친다. 입력 데이터를 (N * out_h * out_w, pool_h * pool*w) 크기로 변환하여 풀링 연산을 쉽게 처리할 수 있도록 준비한다.
      • im2col: 합성곱에서와 마찬가지로 입력 데이터를 각 풀링 영역에 맞게 펼쳐주는 역할을 한다.
  • 최대 풀링 연산
    • 각 풀링 영역(col)에 대해 최댓값을 구한다. np.max(col, axis=1)을 사용해 풀링 영역의 최댓값을 선택하여 out 배열에 저장한다.
  • 출력 형태 변환
    • out을 (N, out_h, out_w, C) 형태로 변경한 후 (N, C, out_h, out_w)로 전치해 최종 출력을 얻는다.

CNN 구현하기

간단한 CNN 클래스

class SimpleConvNet:
    def __init__(self, input_dim=(1, 28, 28),
                 conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
                 hidden_size=100, output_size=10, weight_init_std=0.01):

        filter_num = conv_param['filter_num']
        filter_size = conv_param['filter_size']
        filter_pad = conv_param['pad']
        filter_stride = conv_param['stride']
        input_size = input_dim[1]
        conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
        pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))

        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
        self.params['b1'] = np.zeros(filter_num)
        self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        self.layers = OrderedDict()
        self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad'])
        self.layers['Relu1'] = Relu()
        self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
        self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
        self.layers['Relu2'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
        self.last_layer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        return x

    def loss(self, x, t):
        y = self.predict(x)
        return self.last_layer.forward(y, t)

    def accuracy(self, x, t, batch_size=100):
        if t.ndim != 1:
            t = np.argmax(t, axis=1)

        acc = 0.0
        for i in range(int(x.shape[0] / batch_size)):
            tx = x[i*batch_size:(i+1)*batch_size]
            tt = t[i*batch_size:(i+1)*batch_size]
            y = self.predict(tx)
            y = np.argmax(y, axis=1)
            acc += np.sum(y == tt)

        return acc/ x.shape[0]

    def gradient(self, x, t):
        self.loss(x, t)

        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        grads = {}
        grads['W1'] = self.layers['Conv1'].dW
        grads['b1'] = self.layers['Conv1'].db
        grads['W2'] = self.layers['Affine1'].dW
        grads['b2'] = self.layers['Affine1'].db
        grads['W3'] = self.layers['Affine2'].dW
        grads['b3'] = self.layers['Affine2'].db

        return grads
    
    
    # 모델 저장 및 로딩 methods
    def save_params(self, file_name="params.pkl"): 
        params = {}
        for key, val in self.params.items(): params[key] = val
        with open(file_name, 'wb') as f: pickle.dump(params, f)

    def load_params(self, file_name="params.pkl"):
        with open(file_name, 'rb') as f: params = pickle.load(f)
        for key, val in params.items(): self.params[key] = val

        for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
            self.layers[key].W = self.params['W' + str(i+1)]
            self.layers[key].b = self.params['b' + str(i+1)]

• __init__ 메서드 (초기화)
  - 입력 인자
  - input_dim: 입력 데이터의 차원. 기본적으로 (1, 28, 28)이 설정되어 있어 MNIST 같은 흑백 이미지의 입력 차원에 맞춰져 있다.
  - conv_param: 필터 수, 필터 크기, 패딩, 스트라이드 설정을 포함하는 합성곱 계층의 파라미터.
  - hidden_size: 은닉층의 크기.
  - output_size: 최종 출력 크기. 클래스 수를 나타낸다.
  - weight_init_std: 가중치 초기화 표준 편차로, 가중치 초기값이 설정된다.
  • 네트워크 구조 설정
    • self.params: 신경망 파라미터를 저장하는 딕셔너리. 가중치와 편향 값을 담고 있다.
      • self.layers: 순서가 있는 딕셔너리(OrderedDict). 합성곱 계층(Conv1), ReLU 계층, 풀링 계층, 두 개의 완전 연결 계층과 활성화 계층을 차례로 추가한다.
      • self.last_layer: 소프트맥스와 손실 계산을 수행하는 SoftmaxWithLoss 계층.
• predict 메서드 (예측)
  - 입력 x를 받아 각 계층의 forward 메서드를 통해 순전파를 수행하고, 최종 예측 값을 반환한다. 예측 단계에서는 손실을 계산하지 않는다.
• loss 메서드 (손실 계산)
  - predict 메서드를 통해 예측을 수행한 후 마지막 계층 SoftmaxWithLoss를 통해 예측 값 y와 실제 레이블 t 간의 손실을 계산하여 반환한다.
• accuracy 메서드 (정확도 계산)
  - 입력 데이터 x와 레이블 t의 정확도를 계산한다.
  • 미니 배치 단위로 예측을 수행하여 정확도를 효율적으로 계산한다.
• gradient 메서드 (기울기 계산)
  - 손실 계산을 먼저 수행하고 마지막 계층부터 역순으로 각 계층의 backward 메서드를 호출하여 기울기를 계산한다.
  • 각 계층에서 계산된 기울기를 grads 딕셔너리에 저장하고 반환한다.
• save_params, load_params 메서드 (모델 저장 및 로드)
  - save_params: 파라미터를 파일(params.pkl)에 저장.
  • load_params: 저장된 파일에서 파라미터를 불러와 네트워크에 설정한다.

CNN으로 MNIST 학습/검증

import sys, os
sys.path.append(os.pardir)
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.trainer import Trainer

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)

x_train, t_train = x_train[:5000], t_train[:5000] # 실험에 따라 조정 가능
x_test, t_test = x_test[:1000], t_test[:1000]

max_epochs = 20

network = SimpleConvNet(input_dim=(1, 28, 28),
                        conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
                        hidden_size=100, output_size=10, weight_init_std=0.01)

trainer = Trainer(network, x_train, t_train, x_test, t_test,
                    epochs=max_epochs, mini_batch_size=100,
                    optimizer='Adam', optimizer_param={'lr': 0.001},
                    evaluate_sample_num_per_epoch=1000)
trainer.train()

network.save_params("params.pkl") # 매개변수 보존
print("Saved Network Parameters!")

x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, label='train')
plt.plot(x, trainer.test_acc_list, label='test')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

• 라이브러리 및 데이터 로드
  - 필요한 라이브러리 불러오기.
  • load_mnist: MNIST 데이터셋을 로드하여 train 데이터와 test 데이터로 나눈다.
  • 학습 데이터와 테스트 데이터의 크기를 조절. 학습에 사용할 데이터 양을 설정한다. 나는 학습 5000개
• 하이퍼파라미터 설정
  - max_epochs = 20: 최대 학습 횟수 설정.
• 네트워크 생성
  - SimpleConvNet: CNN 모델 생성.
  • conv_param: 합성곱 계층의 필터 수, 필터 크기, 패딩, 스트라이드 설정을 정의.
  • hidden_size, output_size: 완전 연결 계층의 노드 수, 최종 출력 클래스의 수.
  • weight_init_std=0.01: 가중치 초기화.
• 학습기 설정 및 학습 수행
  - Trainer: 학습 설정.
  • optimizer='Adam', lr=0.001: Adam 최적화 알고리즘 사용.
  • mini_batch_size=100: 미니 배치 학습 수행.
  • trainer.train(): 학습 시작. 각 에포크에서 정확도와 손실 평가.
• 모델 저장
  - network.save_params('params.pkl'): 학습된 모델 파라미터 저장.
• 학습 정확도 시각화
  - train_acc_list와 test_acc_list를 그래프로 시각화하여 학습 경과를 확인.
  - X축은 에포크 수, Y축은 정확도. 그래프가 우상향하면서 학습 및 테스트 정확도가 높아지는지 확인할 수 있다.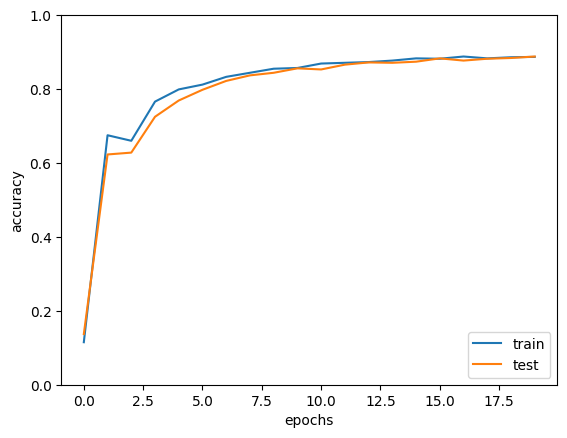

  ![](https://velog.velcdn.com/images/faith_coder_lab/post/011eefba-0c74-45e3-a4f6-84ea4a9bd3e5/image.jpg)

  중간에 학습률을 0.0001로 잘못 설정하여 튀는 그래프가 생성되었다.

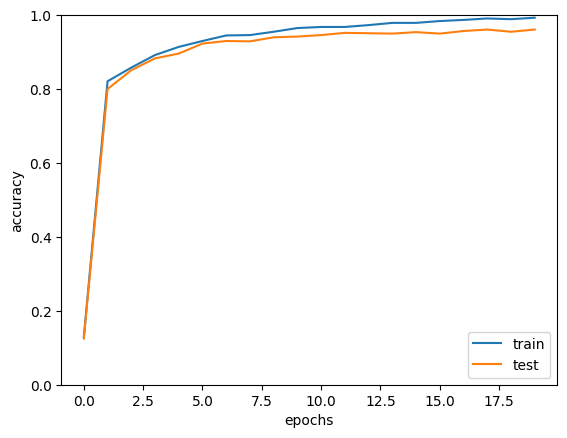
학습률을 0.001로 수정.

학습 전후 시각화

import numpy as np
import pickle
import matplotlib.pyplot as plt

def filter_show(filters, nx=8, margin=3, scale=10):
    FN, C, FH, FW = filters.shape
    ny = int(np.ceil(FN / nx))

    fig = plt.figure()
    fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)

    for i in range(FN):
        ax = fig.add_subplot(ny, nx, i+1, xticks=[], yticks=[])
        ax.imshow(filters[i, 0], cmap=plt.cm.gray_r, interpolation='nearest')
    plt.show()

network = SimpleConvNet()

# 랜덤 초기화 후의 가중치 표시
filter_show(network.params['W1'])

network.load_params('params.pkl')

# 학습 후의 가중치 표시
filter_show(network.params['W1'])

• 필터 시각화 함수 정의(filter_show)
  - filters 배열을 입력으로 받아 필터들을 이미지 형태로 출력.
  • nx: 한 행에 표시할 필터 수. ny는 자동으로 계산된다.
  • fig.subplots_adjust: 필터 이미지 간 여백 설정. / ax.imshow: 각 필터를 회색조로 표시.
• 네트워크 초기화 및 필터 확인
  - network = SimpleConvNet(): SimpleConvNet 인스턴스 생성, CNN 모델 초기화.
• 초기 가중치 시각화
  - 학습 전 필터(network.params['W1'])를 filter_show 함수로 시각화 하여 랜덤 초기화 상태의 필터를 확인한다.
• 학습된 파라미터 로드 및 시각화
  - network.load_params('params.pkl'): 저장된 학습 파라미터 불러오기.

  • filter_show 함수를 사용해 학습 후 첫번째 합성곱 계층의 필터를 시각화하여 학습 전과 비교.

    

대표적 CNN 소개

LeNet (1998, Yann LeCun)

• 초기의 CNN 구조로 숫자 인식을 위해 개발되었다. MNIST와 같은 손글씨 숫자 인식 데이터셋에서 성공적인 성과를 보였다.
• 비교적 얕은 신경망 구조로 6개 레이어로 이루어져 있으며 활성화 함수 sigmoid를 사용하고 average pooling으로 이미지 크기를 줄인다.
• 현대 CNN의 기본적 개념을 제공하였고 합성곱과 풀링 계층을 사용한 최초의 성공적 모델 중 하나.

AlexNet (2012)

• ImageNet 데이터셋에서 이미지 분류 성능을 획기적으로 개선한 CNN 구조로 대규모 이미지 데이터에 대한 학습을 통해 딥러닝의 가능성을 증명했다.
• 8개 레이어로 구성되었으며 ReLU 활성화 함수와 max pooling을 사용했다. 또한 dropout을 도입해 과적합을 방지하였다.
• GPU를 활용하여 더 깊은 구조를 빠르게 학습시킬 수 있었고 이로 인해 딥러닝이 널리 사용되는 계기가 되었다.

VGGNet(2014, Visual Geometry Group)

• 옥스퍼드 대학의 VGG 팀에서 개발된 모델로 심플한 구조로 깊은 신경망을 구성할 수 있는 가능성을 보여주었다.
• 16층(VGG16) 또는 19층(VGG19)의 깊은 구조를 가졌다. 모든 합성곱 계층에 3*3 필터를 사용하여 계산 효율을 높였다.
• 복잡한 구조 없이도 단순한 필터와 레이어의 반복만으로 뛰어난 성능을 낼 수 있음을 증명하였고, 이후 많은 네트워크 모델의 기초가 되었다.

GoogleNet (2014, Inception 모델)

• Google에서 개발한 모델로 ImageNet 대회에서 우승한 모델. 여러 크기의 필터를 동시에 사용하는 Inception 모듈을 도입해 효율적으로 다양한 특성을 추출할 수 있도록 했다.
• 22개의 레이어로 구성되었고, 병렬적인 구조를 활용하여 효율을 극대화하였다.
• Inception 모듈을 통해 서로 다른 크기의 필터를 동시에 적용해 이미지의 특징을 더욱 풍부하게 추출할 수 있다.

정확도 높이기

더 깊은 신경망 구조 사용

• 작은 필터 반복 사용: 3*3과 같은 작은 필터를 여러 층에서 반복 사용하여 복잡한 패턴을 학습할 수 있도록 한다. 작은 필터를 쌓아 깊은 신경망을 구성하면 모델이 다양한 크기의 패턴을 점진적으로 학습하며 더 정교한 특징을 인식할 수 있다.
• 활성화 함수 ReLU: 신경망의 비선형성을 유지하면서도 학습 속도를 빠르게 하는 활성화 함수로, 깊은 네트워크에서도 효과적으로 작동한다.
• 드롭아웃(Dropout): 학습 과정에서 무작위로 일부 뉴런을 꺼 학습하는 기법으로 과적합을 방지하는 데 유리하다. 드롭아웃을 통해 신경망이 다양한 경로를 통해 데이터를 학습하게 할 수 있어 일반화 성능을 높일 수 있다.
• 최적화 기법(Optimizer): Adam과 같은 최적화 기법을 사용하여 학습 속도를 높이고 더 나은 성능을 얻을 수 있다. 최적화 기법은 가중치를 조정하여 모델이 더 빠르게 수렴하도록 돕는다.
• 가중치 초기화: 적절한 가중치 초기화를 통해 깊은 네트워크가 효율적으로 학습되도록 돕는다. 초기 가중치를 잘 설정하면 학습 초기의 불안정성을 줄이고 더 빠르게 수렴할 수 있다.

데이터 증강 (Data Augmentation)

• 데이터셋의 크기를 인위적으로 늘리는 방법으로 이미지 데이터에 다양한 변형을 가하여 더 많은 학습 데이터를 생성한다.
• 데이터 증강은 모델이 다양한 상황에서 견고한 특징을 학습하도록 하여 일반화 성능을 높여준다.

이 부분은 PPT에는 나와있는데 내가 잠깐 졸았던지 배운 기억이 없다,,

전이학습과 Resnet

신경망 복습

신경망과 퍼셉트론

퍼셉트론(Perceptron)은 인공 신경망의 기본 단위로 인간의 뉴런을 모델링한 개념이다. 각 입력값에 가중치를 곱해 더한 값이 특정 임계값을 넘으면 활성화되어 출력 신호를 생성한다.
1. 입력값과 가중치의 결합: 각 입력값에 가중치를 곱하고 이를 모두 더해 선형 결합을 만든다.
2. 임계값(Threshold): 결합한 값이 임계값(또는 편향)을 넘으면 1, 넘지 않으면 0으로 출력을 결정한다.
퍼셉트론은 AND, OR 같은 선형 분류 문제를 해결할 수 있지만, XOR 같은 비선형 문제는 해결하지 못하는 한계가 있다. 이를 극복하기 위해 여러 퍼셉트론을 쌓아 다층 퍼셉트론(MLP)을 구성하게 되었다.

DNN (Deep Neural Network)

심층 신경망은 입력층과 출력층 사이에 여러 개의 은닉층(Hidden Layer)이 추가된 신경망이다. 이 은닉층들은 비선형 활성화 함수를 통해 입력 데이터의 복잡한 패턴을 학습하며 층이 깊어질수록 더 추상적인 특징을 추출할 수 있다.
DNN은 순전파(Forward Propagation)와 역전파(Backpropagation) 과정으로 학습한다. 순전파에서 입력이 각 층을 거치면서 출력이 계산되고, 역전파에서는 예측값과 실제값 간의 오차를 최소화하기 위해 가중치를 조정한다. 이러한 과정에서 경사 하강법 같은 최적화 기법이 사용된다.

활성화 함수 (Activation Function)

신경망에서 중요한 활성화 함수들은 비선형성을 추가하여 복잡한 패턴 학습을 가능하게 한다. Sigmoid, ReLU, Softmax 등이 자주 사용된다. Sigmoid는 기울기 소실(Vanishing Gradient) 문제를 일으킬 수 있어 대체로 ReLU가 선호된다.

오차역전파법 (Backpropagation)

순전파로 예측한 값과 실제 값 간의 오차를 계산하고 역전파를 통해 가중치를 갱신하는 과정. 경사 하강법을 통해 오차를 최소화하며 학습을 진행한다.

Optimizer (최적화 기법)

딥러닝 모델이 학습할 때 가중치와 편향을 효과적으로 조정해 오차를 최소화하는 방법. 최적화 기법은 모델이 손실함수의 값을 줄여 최적의 성능을 내도록 돕는다.
1. 경사 하강법(Gradient Descent): 오차가 줄어드는 방향으로 가중치를 조금씩 업데이트하는 기본 방법.
2. SGD(Stochastic Gradient Descent): 경사하강법의 변형으로 전체 데이터가 아닌 일부 데이터(미니배치)로 가중치를 조정해 연산 속도를 높인다.

• Adam(Adaptive Moment Estimation): 학습률을 데이터와 시간에 따라 조정해 빠르고 효율적으로 학습을 진행한다.

CNN (Convolutional Neural Network)

이미지와 같은 2D 데이터의 특징을 효과적으로 추출하고 분석하기 위해 개발된 신경망 구조.
1. Convolution Layer(합성곱 계층): 이미지의 특정 패턴이나 특징을 추출하기 위해 필터(커널)를 사용해 입력 데이터와 합성곱 연산을 수행한다.
2. Pooling Layer(풀링 계층): 합성곱 층에서 추출된 특징을 압축해 중요한 정보를 강조하고 연산량을 줄인다.
3. Fully Connected Layer(완전 연결 계층): Flatten 과정을 통해 1차원 벡터로 변환된 데이터를 받아 최종 분류 작업을 수행한다.

딥러닝의 학습 단위

학습 단위로 배치(Batch)와 에폭(Epoch)을 설정하며 배치 정규화(Batch Normalisation) 등을 통해 학습 속도를 높인다.

전이학습 (Transfer Learning)

한 신경망 모델이 특정 작업에 대해 학습한 지식(특징)을 유사한 다른 작업에 적용하는 기법. 새로운 문제를 처음부터 학습하지 않고 기존 모델의 학습된 가중치나 구조를 활용해 더 빠르고 효과적으로 학습할 수 있다.

전이학습의 핵심 과정

1. 사전 학습된 모델 활용: 이미지 분류 모델 등에서 사전에 학습된 모델을 가져온다. 이 모델은 일반적인 특징을 이미 학습한 상태.
2. 특정 작업에 맞춤 조정
   • Feature Extraction: 기존 모델의 특정 층까지만 사용하고 새로운 데이터에 맞는 출력층만 추가해 학습.
   • Fine-Tuning: 기존 층들의 일부 가중치를 고정하지 않고 새로운 데이터에 맞게 세밀히 재학습하여 성능을 높인다.

ResNet (Residual Network)

딥러닝 모델의 층이 깊어질수록 발생하는 성능 저하 문제를 해결하기 위해 개발된 신경망 구조. ResNet은 층을 깊게 쌓더라도 학습이 원활하게 이루어지도록 Residual Block이라는 구조를 사용한다.

ResNet의 핵심 개념

1. Residual Block: 입력을 곧바로 출력으로 연결하는 지름길(Shortcut Connection) 을 추가해 입력 정보가 변하지 않고 다음 층으로 전달되도록 한다. 이를 통해 층이 깊어져도 오차가 누적되지 않고 학습이 안정적으로 진행된다.
2. Bottleneck 구조: ResNet-50, ResNet-101 등 깊은 모델에서는 1*1 합성곱을 사용해 연산을 줄이고 학습 효율을 높이는 Bottleneck 구조를 사용한다. 이는 높은 성능을 유지하면서도 계산 비용을 줄여준다.
3. Downsampling: 특정 구간에서 데이터 크기를 줄여 가중치나 계산량을 효율화하며 1*1 합성곱이나 풀링을 통해 채널 크기를 조정한다.

ResNet50

50개의 층으로 이루어진 ResNet 계열의 신경망 모델로 Residual Block과 Botleneck 구조를 통해 깊은 층에서도 학습이 효과적으로 이루어지도록 설계되었다.
1. Residual Block 사용: 입력값을 출력에 바로 전달하는 지름길 연결로 기울기 소실 문제를 해결해 층이 깊어도 학습이 안정적이다.
2. Bottleneck 구조: 1*1 합성곱을 사용해 데이터 차원을 줄이고 연산 효율을 높이면서 성능을 유지한다.
3. 전이학습 활용: 다양한 이미지 데이터셋에 대해 사전 학습된 모델로 제공되어 전이학습을 통해 새로운 이미지 분류 문제에 빠르게 적용할 수 있다.

암석 식별 머신 구현

환경설정만 마쳤다.