스물여섯번째 수업 | 인공신경망 기초 | 퍼셉트

Faithful Dev·2024년 10월 22일

Microsoft Korea 5th AI School

목록 보기

31/59

강명호 강사님

퍼셉트론

뉴런과 퍼셉트론

퍼셉트론은 인간의 뇌 신경세포(뉴런) 를 본떠 만든 인공지능의 기본 모델이다. 뉴런은 신호를 받아들이고 일정한 값을 넘으면 다음 뉴런으로 신호를 보낸다. 퍼셉트론도 비슷한 원리로 작동한다.
퍼셉트론은 입력값과 가중치를 더해 계산한 값이 임계값(θ, theta)보다 크면 1, 작거나 같으면 0을 출력한다.

$y = 1, \text{if } (x_1 * w_1 + x_2 * w_2 + \cdots + b) > 0$
$y = 0, \text{if} (x_1 * w_1 + x_2 * w_2 + \cdots + b) <= 0$
여기서 x는 입력값, w는 각 입력에 곱해지는 가중치, b는 편향값이다.

AND, OR, NAND 게이트

퍼셉트론을 이용해서 간단한 논리 연산을 할 수 있다.

AND 게이트

두 입력값이 모두 1일 때만 1을 출력하고 나머지는 0을 출력한다.

# coding: utf-8
import numpy as np

def AND(x1, x2):
	x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
    	return 0
    else:
    	return 1

if __name__ == '__main__':
	for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
    	y = AND(xs[0], xs[1])
        print(str(xs) + ' -> ' + str(y))

def AND(x1, x2)
- x = np.array([x1, x2]): 입력값 x1과 x2를 NumPy 배열로 만든다. 이렇게 하면 배열 연산이 쉬워진다.
- w = np.array([0.5, 0.5]): 가중치 w를 정의한다. 여기서 0.5는 각각의 입력에 곱해질 가중치이다.
- b = -0.7: 편향(bias) 값을 설정한다. 이 값은 출력에 추가되는 상수로, 신호가 특정 임계값을 넘는지를 조절하는 역할을 한다.
- tmp = np.sum(w*x) + b: 입력값과 가중치를 곱한 후, 그 합에 편향 b를 더한다.
if __name__ = '__main__': 스크립트가 직접 실행될 때만 실행되는 코드. 모듈로 import 될 경우에는 실행되지 않는다.
- for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]: 가능한 모든 입력 조합을 생성한다.
- y = AND(xs[0], xs[1]): 각 입력 조합에 대해 AND 함수를 호출하고 그 결과를 출력한다.

OR 게이트

입력값 중 하나라도 1이면 1을 출력한다.

# coding: utf-8
import numpy as np

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = OR(xs[0], xs[1])
        print(str(xs) + ' -> ' + str(y))

def OR(x1, x2)
- b = -0.2: 편향(bias) 값을 설정한다. OR 게이트에서 편향값은 -0.2로, 출력이 1이 될 기준을 결정하는 값이다.

NAND 게이트

AND 게이트의 반대. 입력이 모두 1일 때만 0을 출력하고, 나머지는 1을 출력한다.

# coding: utf-8
import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = NAND(xs[0], xs[1])
        print(str(xs) + ' -> ' + str(y))

def NAND(x1, x2)
- b = 0.7: 편향(bias) 값을 0.7로 설정한다. 이 값은 출력을 조정하는 상수 역할을 한다.

퍼셉트론의 한계와 다층 퍼셉트론(MLP)

퍼셉트론은 간단한 문제(AND, OR 등)는 해결할 수 있지만, XOR 게이트 같은 복잡한 문제는 해결할 수 없다. XOR은 입력값이 서로 다를 때 1을 출력하는데, 퍼셉트론으로는 이 문제를 해결할 수 없다.
이 한계를 극복하기 위해 다층 퍼셉트론(MLP) 등장. MLP는 여러 퍼셉트론을 층층이 쌓아 복잡한 문제를 해결할 수 있다.

XOR 게이트

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + ' -> ' + str(y))

XOR 함수: 두 입력 x1, x2를 받아 XOR 연산을 수행한다.
s1: 입력값을 NAND 게이트에 통과시켜 얻은 중간 결과. NAND는 두 입력이 모두 1일 때만 0을 반환하고, 나머지는 1을 반환한다.
s2: 입력값을 OR 게이트에 통과시킨 값. OR 게이트는 두 입력 중 하나라도 1이면 1을 반환한다.
y: s1과 s2 값을 AND 게이트에 통과시킨 결과. AND 게이트는 두 입력이 모두 1일 때만 1을 반환한다.
최종적으로 XOR 연산의 결과를 반환한다.

신경망 (Neural Network)

신경망은 사람의 뇌 신경 세포가 서로 연결되어 정보를 처리하는 방식에서 영감을 받아 만들어진 모델이다. 컴퓨터가 데이터를 처리하고 학습하도록 도와준다. 신경망은 퍼셉트론(Perceptron)이라는 가장 기본적인 단위로 시작되고, 이를 연결해 더 복잡한 문제를 해결한다.

퍼셉트론(Perceptron)

퍼셉트론은 가장 간단한 신경망 모델로, 하나의 입력을 받아 처리한 후 결과를 출력한다. 이때 입력에 따라 출력을 결정하는 것이 활성화 함수(Activation Function) 이다.

활성화 함수(Activation Function)

활성화 함수는 입력된 데이터를 기준으로 변형해 출력한다.

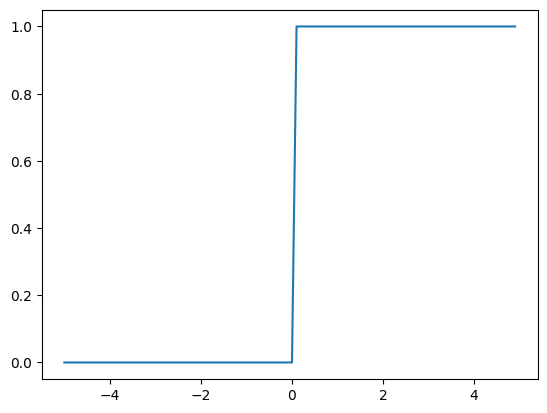
계단 함수

입력 값이 특정 기준을 넘으면 1, 넘지 않으면 0을 출력하는 단순한 함수이다.

def step_function(x):
    if x > 0:
        return 1
    else:
        return 0

def step_function(x): 입력 x를 받아서 계단 함수를 구현하는 함수.
- x > 0: x가 0보다 크면 True, 그렇지 않으면 False를 반환.
- y.astype(np.int64): True를 1로, False를 0으로 변환하여 정수 배열로 반환. 이 배열이 계단 함수의 출력 값이 된다.
x = np.arange(-5.0, 5.0, 0.1): -5부터 5까지 0.1 간격으로 수를 생성하는 NumPy 함수. 이 값들이 계단 함수의 입력으로 들어간다.
y = step_function(x): step_function(x)를 호출하여 x 값에 대한 계단 함수의 출력 y 값을 계산.
plt.plot(x, y): x 축에 x, y 축에 y 값을 이용해 그래프를 그린다.

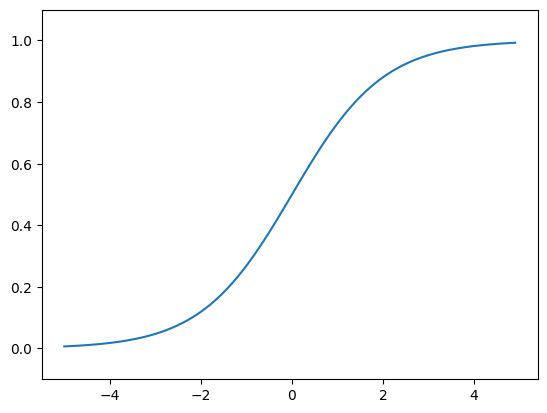
시그모이드 함수

입력을 0에서 1 사이의 값으로 변환하여 확률처럼 표현하는 함수.

# coding: utf-8
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)

plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

def sigmoid(x)
- np.exp(-x): 입력 x의 음수 값에 대한 지수(exponential) 함수를 계산한다.
- 이 함수는 입력 값을 0과 1사이로 변환한다. 음수 값일수록 출력이 0에 가까워지고, 양수 값일수록 출력이 1에 가까워진다.

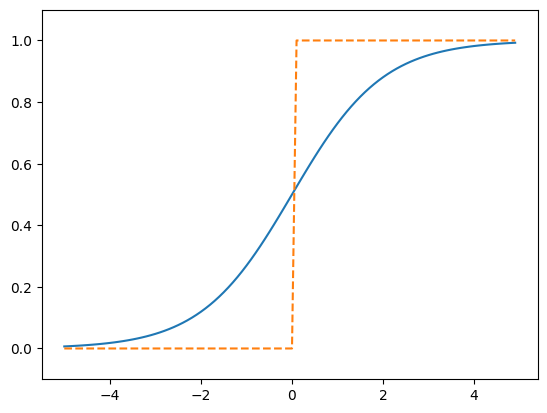
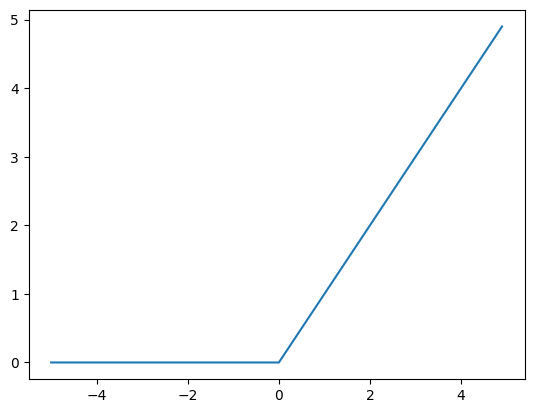
ReLU 함수

입력이 0보다 크면 그대로 출력하고, 작으면 0을 출력한다. 계산이 간단하고 효율적이다.

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt

def ReLU(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = ReLU(x)

plt.plot(x,y)
plt.show()

def ReLU(x): ReLU 함수는 REctified Linear Unit의 약자로 딥러닝에서 많이 사용하는 활성화 함수이다.
- 이 함수는 입력 값 x가 0보다 크면 그대로 출력하고, 0보다 작으면 0을 출력한다. 즉 np.maximum(0, x)는 0과 x 중 더 큰 값을 반환한다.

다차원 배열

다차원 배열은 여러 차원으로 이루어진 데이터 구조로 주로 행렬(matrix) 라고 불린다. 신경망에서는 입력 데이터, 가중치, 출력 등을 행렬로 표현하고, 이들 간의 연산을 통해 학습이 이루어진다. 여기서 '차원'은 배열의 구조가 얼마나 복잡한지 나타낸다.

배열의 차원수(ndim)

배열의 차원수를 나타내는 속성은 ndim이다.

배열의 형상(shape)

배열의 형상은 각 차원에서 배열의 크기를 말한다.
배열의 형상은 shape 속성으로 확인할 수 있다.

다차원 배열의 사용

스칼라(Scalar): 0차원 배열, 단일 값
벡터(Vector): 1차원 배열, 값들의 리스트
행렬(Matrix): 2차원 배열, 행과 열로 구성된 배열
3차원 배열(Tensor): 여러 개의 2차원 배열이 모인 구조

3층 신경망

입력층(Input Layer): 데이터를 받아들이는 층.
은닉층(Hidden Layer): 입력층과 출력층 사이에 있는 중간 층. 이 층에서는 데이터를 변환하고 처리하는 역할을 한다. 은닉층이 많아질수록 신경망은 더 복잡한 패턴을 학습할 수 있다.
출력층(Output Layer): 신경망이 최종적으로 예측하는 결과를 출력하는 층.

신경망의 신호 전달

3층 신경망에서는 각 층에서 신호가 전달되고 가중치와 활성화 함수가 적용된다. 이를 순전파(Forward Propagation) 라고 부른다.

입력층에서 1층 은닉층으로 신호 전달
- 입력 데이터를 가중치와 곱하고 편향(bias)을 더한 후 활성화 함수를 적용하여 은닉층으로 전달한다.
- A1 = W1 * X + B1
  - X: 입력 데이터 (입력층에서 받은 값)
  - W1: 1층 가중치
  - B1: 1층 편향
  - A1: 은닉층에 전달되는 신호
1층 은닉층에서 2층 은닉층으로 신호 전달
- 은닉층에서 또 다른 가중치와 편향이 적용된 후 활성화 함수를 통해 다음 층으로 신호가 전달된다.
- A2 = W2 * H1 + B2
  - H1: 1층 은닉층에서 나온 출력
  - W2: 2층 가중치
  - B2: 2층 편향
  - A2: 2층에 전달되는 신호
2층 은닉층에서 출력층으로 신호 전달
- 마지막 은닉층에서 출력층으로 신호가 전달되고 최종 결과가 출력된다.
- Y = W3 * H2 + B3
  - H2: 2층 은닉층의 출력
  - W3: 출력층으로의 가중치
  - B3: 출력층의 편향
  - Y: 최종 출력 값

역전파(Backpropagation)

신경망이 학습할 때 사용하는 알고리즘으로, 예측값과 실제값의 차이를 계산한 후 그 차이를 각 층으로 되돌려 보내면서 가중치와 편향치를 조정한다. 역전파는 각 가중치가 예측에 얼마나 기여했는지에 대한 정보를 바탕으로 가중치를 업데이트하여 신경망이 점점 더 정확한 예측을 할 수 있도록 학습한다.

3층 신경망 학습 과정

순전파(Forward Propagation): 입력 데이터를 신경망에 넣고 각 층을 거치며 출력값을 계산.
손실 함수(Loss Function) 계산: 출력값과 실제값의 차이를 계산. 이 차이를 줄이기 위해 학습이 이루어진다.
역전파(Bakpropagation): 손실 함수로 계산된 오차를 바탕으로 가중치와 편향을 조정한다.
반복(Iteration): 이 과정을 여러 번 반복하여 신경망이 점점 더 나은 예측을 할 수 있도록 만든다.

import numpy as np

X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])

print(X.shape)
print(W1.shape)
print(B1.shape)

입력 데이터 X
- 1차원 배열로, 두 개의 요소 [1.0, 0.5]를 가진다.
- X.shape는 (2,)로 출력된다. 즉 X는 1차원 배열.
가중치 행렬 W1
- 2차원 배열로, 2*3 크기의 행렬이다.
- W1.shape는 (2, 3)으로 출력된다. (2개의 행, 3개의 열)
- 신경망에서 입력 데이터를 변환할 때 가중치 행렬은 각 층의 노드 간의 연결 강도를 나타내며 입력 데이터를 가중합으로 변환하는 역할을 한다.
편향 벡터 B1
- 1차원 배열로, 3개의 요소 [0.1, 0.2, 0.3]을 가진다.
- B1.shape는 (3,)으로 출력된다.
- 편향은 신경망에서 입력 데이터에 더해져 신호를 조정하는 역할을 한다.

A1 = np.dot(X, W1) + B1
print(A1)

신경망에서 입력 데이터와 가중치를 곱한 후 편향을 더하는 과정. 결과로 은닉층에 전달되는 신호를 계산할 수 있다.

def sigmoid(x) :
    return 1 / (1 + np.exp(-x))

Z1 = sigmoid(A1)

print('A1 = ', A1)
print('Z1 = ', Z1)

def sigmoid(x): 시그모이드 함수 정의
- 시그모이드 함수는 입력값 x를 0과 1 사이의 값으로 변환하는 비선형 활성화 함수이다.
- 이 함수는 신경망에서 노드의 출력값을 확률처럼 해석할 수 있게 해준다.
  - $\sigma (x) = \frac{1}{1+e^{-x}}$
    - np.exp(-x): 자연상수 e에 대해 x의 음수에 대한 지수 함수를 계산하는 것
Z1 = sigmoid(A1): A1 값을 시그모이드 함수로 변환
- A1은 이전 계산에서 나온 값
- 시그모이드 함수에 A1을 입력으로 넣으면 A1의 각 요소가 0과 1 사이의 값으로 변환된다.

W2 = np.array([[0.1,0.4], [0.2,0.5], [0.3,0.6]])
B2 = np.array([0.1,0.2])

print(Z1.shape)
print(W1.shape)
print(B1.shape)

A2 = np.dot(Z1, W2) + B2
print('A2 = ', A2)
Z2 = sigmoid(A2)
print('Z2 = ', Z2)

W2, B2: 가중치와 편향 설정
A2 = np.dot(Z1, W2) + B2: A2 계산 (두 번째 은닉층의 입력 신호)
Z2 = sigmoid(A2): A2를 시그모이드 함수로 변환

def identity_function(x) :
    return x

W3 = np.array([[0.1,0.3], [0.2,0.4]])
B3 = np.array([0.1,0.2])

print(Z2.shape)
print(W3.shape)
print(B3.shape)

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)
print('Y = ', Y)

def identity_function(x): 항등 함수 정의
- 항등 함수(Identity Function): 입력값을 그대로 반환하는 함수.
- 출력층에서 사용하는 함수로 회귀 문제처럼 값을 그대로 출력해야 하는 경우에 주로 사용된다. 이 함수는 변환 없이 입력을 그대로 출력으로 전달한다.
W3, B3: 가중치와 편향 설정 (출력층)
A3 = np.dot(Z2, W3) + B3: A3 계산 (출력층 입력 신호)
Y = identity_function(A3): 항등 함수 적용 (A3 = Y)

Faithful Dev

Turning Vision into Reality.

이전 포스트

두번째 MS 타운홀 미팅 | 미니 프로젝트 (게임)

다음 포스트