스물일곱번째 수업 | 인공신경망

강명호 강사님

신경망

3층 신경망

import numpy as np

def init_network() :
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

def forward(network, x) :
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

• init_network(): 신경망의 가중치(W1,W2,W3) 와 편향(b1,b2,b3) 을 설정하고 초기화한다.
  - W1,W2,W3: 각 층에서 입력 데이터를 다음 층으로 전달하는 데 필요한 가중치 행렬
  • b1,b2,b3: 각 층에서 더해지는 편향 값
  • 초기화된 가중치와 편향들은 딕셔너리(network)에 저장되고 네트워크를 구성한다.
• forword: 순전파 함수.
  - 1층 (입력 -> 첫번째 은닉층)
  - a1 = np.dot(x, W1) + b1: 입력 x에 가중치 W1을 곱하고 편향 b1을 더한다.
  - z1 = sigmoid(a1): 시그모이드 함수를 적용, 첫 번째 은닉층의 출력을 계산한다.
  • 2층 (첫번째 은닉층 -> 두번째 은닉층)
    • a2 = np.dot(z1, W2) + b2: 첫번째 은닉층의 출력 z1에 가중치 W2를 곱하고 편향 b2를 더한다.
      • z2 = sigmoid(a2): 시그모이드 함수를 적용, 두번째 은닉층의 출력을 계산한다.
  • 출력층 (두번째 은닉층 -> 출력층)
    a3 = np.dot(z2, W3) + b3: 두번째 은닉층의 출력 z2에 가중치 W3를 곱하고, 편향 b3를 더한다.
    • y = identity_function(a3): 출력층에서는 항등 함수를 사용해 최종 출력을 계산한다.
• sigmoid, identity_function
  - sigmoid(x): 시그모이드 함수는 입력값을 0과 1사이로 변환하는 함수로 각 층의 출력에 비선형성을 추가한다.
  • identity_function(x): 항등 함수는 입력값을 그대로 반환한다. 출력층에서 회귀 문제 같은 경우에는 주로 항등 함수를 사용한다.
• network = init_network(): 네트워크를 초기화하여 가중치와 편향을 설정
• y = forward(network, x): 초기화된 네트워크를 사용하여 입력 데이터를 순전파로 처리하고 최종 출력값 y를 계산한다.

출력층 설계

def softmax(a) :
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

Softmax 함수

Softmax 함수는 신경망 출력층에서 많이 사용되며 출력값을 확률 분포로 변환한다. 즉 입력된 값들을 0과 1 사이의 값으로 변환하여 모든 출력값의 합이 1이 되도록 한다. 주로 다중 클래스 분류 문제에서 사용된다.

• 입력: a는 신경망의 출력층에서 나온 값들
• 출력: y는 입력 값들을 확률로 변환한 값

내용

• exp_a = np.exp(a): 지수 함수로 변환
  - 입력 값 a에 대해 지수 함수 적용
  - np.exp(a): 자연상수 e에 대해 각 요소에 지수 함수를 적용한 값
  - Softmax는 값들이 너무 작거나 클 때 계산상의 문제를 피하기 위해 지수 함수로 값을 확장한 후 처리한다.
• sum_exp_a = np.sump(exp_a): 지수 함수 값들의 합 계산
  - 이 총합은 나중에 각 지수 함수를 정규화하기 위해 사용된다. 이를 통해 모든 출력값이 0과 1 사이로 변환되고, 전체 합은 1이 된다.
• y = exp_a / sum_exp_a: 확률 계산
  - 각 지수 값 exp_a를 그 총합 sum_exp_a로 나누면 값들은 0과 1 사이의 범위로 변환된다.
  • 이렇게 변환된 값들은 확률 분포로 나타내며 이 값들의 합은 항상 1이 된다.

Overflow 문제 해결

Softmax는 값이 매우 크거나 작을 때 오버플로우(Overflow) 문제가 발생할 수 있다. 이를 방지하기 위해 보통 입력값에서 최대값을 빼준다.
강사님께 질문했는데 다음 설명해주실 내용이라고 하셔서 좋은 질문 한 것 같아서 기분이 아주 좋았다.

def softmax(a) :
    c = np.max(a)
    exp_a = np.exp(a-c) # 입력값에서 최대값을 빼서 Overflow 방지
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

손글씨 숫자 인식

라이브러리 임포트

import sys, os
sys.path.append(os.pardir)

from dataset.mnist import load_mnist

• sys.path.append(os.pardir): 현재 디렉토리의 상위 디렉토리를 경로로 추가한다. (dataset.mnist 모듈을 찾기 위해 필요한 설정)

MNIST 데이터셋 로드

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

• load_mnist(): MNIST 데이터를 불러와서 두 개의 튜플을 반환한다.
  - (x_train, t_train): 훈련 데이터(이미지와 레이블)
  • (x_test, t_test): 테스트 데이터(이미지와 레이블)
  • flatten=True: 이미지를 1차원 배열로 변환한다.
  • normalize=False: 이미지 데이터를 정규화하지 않는다. MNIST 이미지의 픽셀은 원래 0에서 255 사이의 값을 가지는데 정규하를 하지 않으면 그대로 0~244 범위의 값이 유지된다.

이미지 시각화

import sys, os
sys.path.append(os.pardir)
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist

def img_show(img):
    plt.imshow(img, cmap='grey')
    plt.axis('off')
    plt.show()

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

img = x_train[0]
label = t_train[0]
print(label)

print(img.shape)
img = img.reshape(28, 28)
print(img.shape)

img_show(img)

• img_show: 입력으로 받은 이미지를 matplotlib 라이브러리로 화면에 출력한다.
  - plt.imshow(img, cmap='grey'): 이미지를 회색조(Greyscale) 로 표시한다.
  • plt.axis('off'): 축을 숨겨서 이미지만 보이도록 한다.
• img = x_train[0], label = t_train[0]
  - x_train[0]: 첫번째 훈련 이미지 데이터. 이 이미지는 1차원 배열로 되어 있다.
  • t_train[0]: 첫번째 이미지에 해당하는 레이블. MNIST는 손글씨 숫자를 인식하기 위한 데이터셋이므로, 레이블은 0~8 사이의 숫자이다.
• img = img.reshape(28, 28): 이미지를 다시 28*28 크기의 2차원 배열로 변환한다.
  

# 한 줄에 모든 요소가 보이도록 linewidth 설정
np.set_printoptions(linewidth=200)

같이 듣는 동기 분이 알려주신! 히히

환경 설정

import sys, os
sys.path.append(os.pardir)

import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax

• sys.path.append(os.pardir): 상위 디렉토리를 Python 모듈 검색 경로에 추가하는 역할을 한다.
  - 이렇게 함으로써 dataset.mnist와 common.functions 모듈을 상위 디렉토리에서 불러올 수 있다. 이 설정은 프로젝트가 여러 디렉토리로 나뉘어 있을 때, 상위 디렉토리나 다른 디렉토리에 있는 파일을 쉽게 참조하기 위해 사용된다.
  

3층 신경망 구현

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

• network 딕셔너리를 사용해 신경망의 가중치(W1, W2, W3)와 편향(b1, b2, b3)을 정의한다.

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

• 입력값 x 는 신경망을 통과하며 각 층에서 가중치와 편향을 적용하고 활성화 함수를 사용하여 변환된다.
• 활성화 함수로는 sigmoid가 사용되었고, 출력층에서는 항등 함수를 사용하였다.

a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)

• 첫번째 은닉층: 입력값 x에 가중치 W1을 곱하고 편향 b1을 더한 후 시그모이드 함수를 적용하여 첫번째 은닉층의 출력을 계산.
• 두번째 은닉층: 첫번째 은닉층 출력 z1에 가중치 W2을 곱하고 편향 b2를 더한 후 시그모이드 함수를 적용하여 두번째 은닉층의 출력 계산.
• 출력층: 두번째 은닉층의 출력 z2에 가중치 W3를 곱하고, 편향 b3을 더한 후 항등 함수를 적용하여 최종 출력을 계산.

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

• init_network(): 신경망을 초기화하고 가중치와 편향을 설정한다.
• x = np.array([1.0, 0.5]): 입력값 x는 2개의 요소로 구성된 1차원 배열이다.
• forward(network, x): 입력값을 신경망에 넣어 순전파를 실행하고 출력값 y를 계산한다.

신경망 추론 처리

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test

테스트 데이터셋을 반환한다.

def init_network():
    with open('sample_weight.pkl', 'rb') as f:
        network = pickle.load(f)
    return network

• sample_weight.pkl 파일에는 학습된 가중치와 편향 값이 저장되어 있다.
• **pickle.load()를 사용해 이 파일에서 가중치와 편향을 불러온다.

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    
    return y

입력 x에 대해 신경망을 통해 순전파를 실행하여 예측 결과를 반환한다.

추론 및 평가

x, t = get_data()  
network = init_network()  

• get_data(): 테스트 데이터(x)와 각 이미지에 해당하는 실제 숫자 레이블(t)을 불러온다.
• init_network(): sample_weight.pkl에서 학습된 가중치와 편향을 불러와 신경망을 초기화한다.

accuracy_cnt = 0 

for i in range(len(x)):
    y = predict(network, x[i]) 
    p = np.argmax(y)  
    if p == t[i]:  
        print('predicted num = ', p, ' Original num = ', t[i])
        accuracy_cnt += 1 

• for i in range(len(x)): x에 있는 테스트 데이터의 개수만큼 반복한다. x[i]는 i번째 테스트 데이터이다.
  - y = predict(network, x[i]): i번째 데이터를 신경망에 입력하여 예측 결과를 계산한다.
  • p = np.argmax(y): 예측된 확률 중 가장 높은 확률을 가진 인덱스를 선택한다.
  • if p == t[i]: 예측 p가 실제 정답 레이블 t[i]와 같으면 정ㅎ왁한 예측으로 간주하고 accuracy_cnt를 1 증가시킨다.

배치 처리

이전 코드에서는 한 번에 한 개의 데이터를 처리했지만 이번에는 배치 크기를 지정하여 여러 데이터를 한 번에 처리하고 정확도를 계산한다. 배치 처리는 속도와 메모리 효율성을 높이기 위해 자주 사용된다.

batch_size = 100 

한 번에 처리할 데이터의 개수를 설정한다. 여기서는 한 번에 100개의 데이터를 처리한다.

accuracy_cnt = 0 

for i in range(0, len(x), batch_size):  
    x_batch = x[i:i+batch_size] 
    y_batch = predict(network, x_batch)  
    p = np.argmax(y_batch, axis=1)  
    accuracy_cnt += np.sum(p == t[i:i+batch_size]) 

• range(0, len(x), batch_size): x의 길이만큼 배치 크기 단위로 반복한다.
  - x_batch = x[i:i+batch_size]: i번째 배치 데이터를 가져온다. x[i:i+batch_size]는 i부터 i+100개의 데이터를 선택하는 슬라이싱이다.
  • y_batch = predict(network, x_batch): 해당 배치 데이터를 신경망에 넣어 예측을 수행한다. predict 함수는 입력된 배치에 대해 확률 분포를 반환한다.
  • p = np.argmax(y_batch, axis=1): 배치 내의 각 데이터에 대해 가장 높은 확률을 가진 클래스의 인덱스를 반환한다. axis=1은 배치에서 각 행에 대해 가장 높은 값을 찾겠다는 의미이다.
• accuracy_cnt += np.sum(p == t[i:i+batch_size]): 예측된 값 p와 실제 레이블 t[i:i+batch_size]을 비교하여 일치하는 값의 개수를 더한다.

print('Accuracy: ' + str(float(accuracy_cnt) / len(x)))

• accuracy_cnt: 정확하게 예측된 데이터의 개수
• 정확도(Accuracy): 전체 데이터 중에서 정확히 예측된 데이터의 비율로 계산된다. 즉 accuracy_cnt / len(x)로 정확도를 계산하고 출력한다.

신경망 학습

손실함수(Loss Function)

손실함수는 신경망이 예측한 값과 실제 값 사이의 차이를 계산하는 함수이다. 이 값이 작을수록 신경망의 성능이 좋다는 뜻!

• 오차제곱합(SSE): 예측값과 실제값의 차이를 제곱해서 더한 값
  $E = \frac{1}{2} \sum_k(y_k - t_k)^2$
• 교차 엔트로피 오차(CEE): 확률 분포 간의 차이를 계산하는 방법으로 정답일 때의 확률을 높이도록 유도한다.
  $E = -\sum_k t_k \log y_k$

오차제곱합

def sum_squares_error(y, t):
	return 0.5 * np.sum((y-t)**2)

예측값과 실제값의 차이를 제곱한 뒤, 그 값을 더해서 손실을 계산한다. 계산된 값이 클수록 예측이 많이 틀렸다는 의미이고, 값이 작으면 예측이 잘 맞았다는 뜻.

• y: 모델이 예측한 값 (출력값)
• t: 실제 값 (정답 레이블)
• (y -t): 예측값에서 실제값을 뺀 차이
• **2: 차이를 제곱한다. 이를 통해 음수와 양수의 차이가 모두 양수로 변환되어 오차 크기를 표현한다.
• 0.5: 수식상의 편의성으로 곱해준다. 경사 하강법에서 미분할 때 계산을 간단하게 해준다.

교차 엔트로피 오차

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

예측값이 실제 값과 얼마나 다른지 확률 분포 간의 차이를 측정한다. 예측 확률이 실제 정답에 가까울수록 값이 작아지고, 반대일 경우 값이 커진다.

• y: 신경망이 예측한 값 (확률값)
• t: 실제 값 (원핫 인코딩된 값)
• delta = 1e-7: delta는 아주 작은 값으로 예측값 y가 0이 되는 것을 방지하기 위해 사용된다. 로그 함수에서 log(0)은 계산할 수 없기 때문에 작은 값을 더해 오류를 막는 역할을 한다.
• np.log(y + delta): 예측값 y에 delta를 더해 로그를 계산한다. 확률값이 클수록 로그값은 작아지고 작을수록 로그값은 커져서 오차가 커지는 형태를 취한다.
• t * np.log(y + delta): 실제값인 t와 로그값을 곱한다. t가 1인 곳에서는 오차가 반영되고 0인 곳에서는 무시된다. 즉 실제 정답인 위치에서만 오차를 계산하는 방식이다.
• -: 교차 엔트로피는 음수 값이 나올 수 있기 때문에 최종값에 마이너스를 붙여 양수로 만든다. 이는 확률 값이 커질수록 오차가 줄어들도록 하기 위함이다.

미니배치 학습과 에폭

모든 데이터를 한 번에 학습하면 시간이 오래 걸리기 때문에 데이터를 작은 그룹(미니배치)으로 나눠서 학습을 진행한다. 이를 통해 학습 속도가 빨라지고 효율적으로 학습할 수 있다. 신경망이 전체 데이터셋을 한 번 학습할때마다 에폭(Epoch) 이 1 증가한다.

MNIST 데이터 로드

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

• x_train, t_train: 학습 데이터와 그에 해당하는 정답 레이블
• x_test, t_test: 테스트 데이터와 그에 해당하는 정답 레이블
• normalize=True: 이미지 데이터를 0~1 사이의 값으로 정규화
• one_hot_label=True: 정답 레이블을 원핫 인코딩(one-hot encoding) 형태로 변환

미니배치 학습

train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]

• batch_size = 10: 미니배치의 크기, 한 번에 10개의 데이터를 무작위로 선택해 학습
• batch_mask = np.random.choice(train_size, batch_size): train 데이터 중에서 10개의 인덱스를 랜덤하게 선택.
• x_batch, t_batch: 선택된 미니배치 데이터와 그에 해당하는 정답 레이블

교차 엔트로피 오차 함수

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    return -np.sum(t * np.log(y + 1e-7)) / batch_size

• y.ndim == 1: 만약 입력 y가 1차원이라면 배치 처리에 맞게 변환.
• batch_size = y.shape[0]: 배치 크기 확인
• -np.sum(...) / batch_size: 배치에 대한 평균 오차를 계산해 반환.

교차 엔트로피 오차 함수 2

레이블이 원핫 인코딩이 아닐 때 (정수형 클래스 인덱스일 때) 사용할 수 있는 교차 엔트로피 오차 함수.

def cross_entropy_error2(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

• y[np.arange(batch_size), t]: y의 예측 값에서 정답에 해당하는 확률을 가져오는 부분.
  - np.arange(batch_size): [0, 1, 2, ..., batch_size-1] 인덱스를 생성
  • t: 정답 레이블. 각 데이터의 정답에 해당하는 확률 값만 추출하게 된다.
• np.log(y[np.arange(batch_size), t] + 1e-7): 해당 확률에 대해 로그를 계산한다.

수치미분

미분의 기본 개념

미분은 어떤 함수의 변화율을 의미한다. 즉 입력값이 아주 조금 변했을 때 출력값이 얼마나 변하는지를 계산하는 과정이다. 고등학교 졸업 후 너무 오랜만이다..

여기서 h는 아주 작은 값이다. 입력 x에서 약간 변한 값 x+h에서의 함수 값 변화가 미분을 통해 구해진다.

수치 미분 (Numerical Derivative)

실제로 h가 극도로 작은 값을 취할 때 함수 f(x)의 미분값을 수치적으로 근사할 수 있다. 수치미분은 이 개념을 기반으로 컴퓨터에서 미분을 계산할 때 유용하게 사용된다.

def numerical_diff(f, x):
    h = 1e-4 # 0.00001
    return (f(x+h) - f(x-h)) / (2*h)

• f: 미분할 함수
• x: 미분을 구할 점
• h = 1e-4: 아주 작은 값으로, h를 작게 설정하여 미분을 근사한다.
• (f(x+h) - f(x-h)) / (2*h): 수치미분 공식으로 기울기를 구하는 방식.
  

def tangent_line(f, x):
    d = numerical_diff(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y

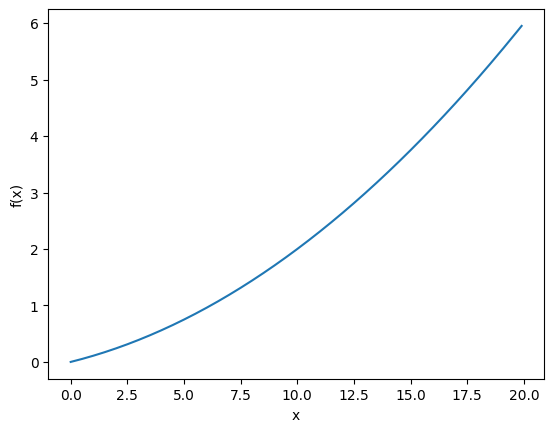
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel('x')
plt.ylabel('f(x)')

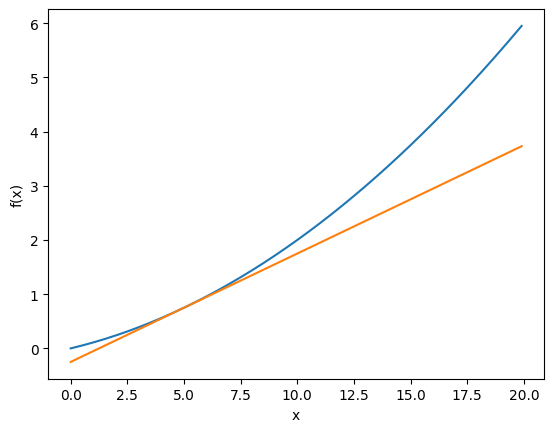
tf = tangent_line(function_1, 5)
y2 = tf(x)

plt.plot(x, y)
plt.plot(x, y2)
plt.show()

• d = numerical_diff(f, x): 기울기 계산. f의 x에서의 기울기 d를 계산한다.
• 접선 방정식은 직선의 방정식 $y = mx + b$ 형식을 따른다. 여기서 m은 기울기 d이고 b는 y절편이다. $f(x) = d*x + b$에서 $b = f(x) - d*x$로 구할 수 있다.
• $y = d*t + y$ 형식으로 접선 방정식을 반환한다. t는 x축의 값이다.
  

편미분 (Partial Derivatives)

각 함수에서 하나의 변수는 고정된 값으로 두고, 다른 변수에 대해서 미분을 수행한다.

def function_tmp1(x0):
    return x0*x0 + 4.0**2.0

이 함수는 $f(x_0) = x^2_0 + 4^2$을 나타낸다. 이 함수에서 x0만 변수로 취급되고 4^2은 상수로 고정되어 있다. 즉 이 함수는 본질적으로 x0에 대한 단일 변수 함수이다.

def function_tmp2(x1):
    return 3.0**2.0 + x1*x1

이 함수는 $f(x_1) = 3^2 + x^2_1$를 나타낸다. 여기서 x1만 변수로 취급되고 3^2는 상수로 고정된 값이다. 즉 이 함수는 x1에 대한 단일 변수 함수이다.

기울기 (Gradient)

다변수 함수에서 모든 변수에 대한 편미분값을 벡터로 나타낸 것. 기울기는 함수의 값이 가장 크게 변하는 방향과 그 크기를 알려준다. 딥러닝에서는 오차 함수(손실 함수)의 기울기를 계산해 그 값을 바탕으로 모델의 가중치와 편향을 업데이트한다. 이를 통해 오차를 줄이고 모델의 성능을 향상시킬 수 있다.

기울기 함수

def numerical_gradient(f, x):
    h = 1e-4  
    grad = np.zeros_like(x)  

• f: 기울기를 계산할 함수.
• x: 함수 f에서 기울기를 계산하려는 변수들의 배열(벡터).
• h = 1e-4: 미분을 근사할 때 사용할 매우 작은 값.
• grad = np.zeros_like(x): x와 같은 형태를 가지며 모든 요소가 0인 배열을 생성한다. 여기에는 나중에 계산된 기울기 값이 저장된다.

    for idx in range(x.size):
        tmp_val = x[idx]
        # f(x+h) 계산
        x[idx] = tmp_val + h
        fxh1 = f(x)
        # f(x-h) 계산
        x[idx] = tmp_val - h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val  # 값 복원

• for idx in range(x.size): x의 각 요소에 대해 반복문을 실행한다. 즉 각 변수에 대해 미분을 수행한다.
• tmp_val = x[idx]: x[idx]의 원래 값을 저장해둔다. 나중에 원래 값으로 복원할 때 사용된다.
• x[idx] = tmp_val + h: x[idx]에 아주 작은 값 h를 더한 후 그 값을 가지고 f(x)를 계산한다.
• x[idx] = tmp_val - h: x[idx]에 아주 작은 값 h를 뺀 후 그 값을 가지고 함수 f(x)를 계산한다.
• grad[idx] = (fxh1 - fxh2) / (2*h): 수치미분 공식 $\frac{f(x+h)-f(x-h)}{2h}을 사용해 x[idx]에서의 미분값(기울기)을 계산한다.
• x[idx] = tmp_val: x를 원래 값으로 복원한다.

시각화

import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

• mpl_toolkits.mplot3d: 3D 그래프를 그리기 위한 도구.

def _numerical_gradient_no_batch(f, x):
    h = 1e-4  # 작은 값
    grad = np.zeros_like(x)  # x와 같은 형상의 배열 생성

    for idx in range(x.size):
        tmp_val = x[idx]

        # f(x+h) 계산
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)

        # f(x-h) 계산
        x[idx] = tmp_val - h
        fxh2 = f(x)

        # 미분값 계산
        grad[idx] = (fxh1 - fxh2) / (2 * h)
        x[idx] = tmp_val  # 원래 값 복원

    return grad

• 단일 데이터에 대한 기울기를 수치적으로 계산한다.
• f(x+h)와 f(x-h)를 이용해 미분값을 계산하는 중앙 차분법을 사용한다.
• 각 변수에 대해 미분을 수행하여 기울기를 계산하고 이를 grad 배열에 저장한다.

def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        for idx, x in enumerate(X):
            print(x)
            grad[idx] = _numerical_gradient_no_batch(f, x)

        return grad

• 배치 데이터를 처리하는 함수로 여러 데이터 점에 대해 기울기를 계산할 수 있다.
• 데이터가 1차원일 경우 개별적으로 numerical_gradient를 호출해 기울기를 계산하고, 2차원 이상의 경우에는 각 데이터에 대해 반복적으로 _numerical_gradient_no_batch를 호출해 기울기를 계산한다.

def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d * x
    return lambda t: d * t + y

• 함수 f(x)의 접선(tangent line) 을 구하는 함수.
• numerical_gradient를 이용해 기울기 d를 계산하고 접선의 방정식을 반환한다.
• 접선 방정식: $y = d \cdot x + (f(x) - d \cdot x)$

if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    x, Y = np.meshgrid(x0, x1)

    X = X.flatten()
    Y = Y.flatten()

    grad = numerical_gradient(function_2, np.array([X, Y]))
    print(grad)

    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1], angles="xy", color="#666666")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.legend()
    plt.draw()
    plt.show()

• Meshgrid 생성
  - x0, x1: -2dptj 2.5까지 0.25 간격으로 값을 가지는 배열.
  • np.meshgrid(x0, x1): 2D 좌표 공간에서 x0과 x1을 만들기 위한 격자(grid)를 생성.
• X = X.flatten(), Y = Y.flatten(): 2차원 배열을 1차원으로 평탄화. 각 좌표에서 기울기를 계산하기 위해 사용된다.
• numerical_gradient(function_2, np.array([X, Y])): 각 좌표에서 기울기를 계산.
• 화살표 플롯
  - plt.quiver(X, Y, -grad[0], -grad[1], angles='xy', color='#666666'): 각 좌표에서 기울기를 화살표로 그려준다.
  • -grad[0], -grad[1]: 기울기의 음수 방향을 나타내며 경사하강법에서 기울기의 반대 방향으로 이동하는 것과 관련이 있다.

경사하강법

def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x

• f: 최적화할 대상이 되는 함수.
• init_x: 초기값. 경사하강법이 시작할 지점이다. 보통 무작위로 시작하거나 특정 값을 지정할 수 있다.
• lr=0.01: 학습률(Learning Rate). 한번의 기울기 계산 후 얼마나 이동할지 결정하는 상수로 값이 너무 크면 발산할 수 있고 너무 작으면 학습이 매우 느려진다.
• step_num=100: 반복 횟수. 경사하강법을 몇 번 반복할지 결정한다. 이 값이 클수록 더 많이 반복하며 최솟값에 가까워진다.

    for i in range(step_num):
        grad = numerical_gradient(f, x)
        x -= lr * grad
    return x

• for i in range(step_num): 경사하강법을 step_num번 반복한다.
• grad = numerical_gradient(f, x): 함수 f의 현재 위치 x에서의 기울기(Gradient) 를 계산한다. 기울기는 현재 위치에서 함수 값이 가장 크게 변화하는 방향을 가리킨다.
• x -= lr * grad: 경사하강법의 핵심 부분. 현재 위치 x에서 기울기 grad의 반대 방향으로 이동한다. 기울기의 반대 방향으로 이동하는 이유는 그 방향이 함수 값을 감소시키는 방향이기 때문. 학습률 lr은 이동할 거리를 조절한다.

시각화

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt

#from gradient_2d import numerical_gradient
def _numerical_gradient_no_batch(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성

    for idx in range(x.size):
        tmp_val = x[idx]

        # f(x+h) 계산
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)

        # f(x-h) 계산
        x[idx] = tmp_val - h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val # 값 복원

    return grad

• 입력: 함수 f, 변수 x.
• 출력: x에서의 기울기(Gradient) 벡터.
• f(x+h)와 f(x-h)를 계산해 미분을 근사한다.

def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)

        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)

        return grad

• 입력: 다차원 배열 x에 대해 각 데이터에서 기울기를 계산한다.
• 출력: 각 데이터에서의 기울기 값을 계산하여 반환한다.

def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append(x.copy())

        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x, np.array(x_history)

• init_x: 경사하강법 초기값.
• lr=0.01: 학습률.
• step_num=100: 반복 횟수.
• x_history: 각 반복마다 변수 x가 어떻게 변해가는지 기록한다.
• x -= lr * grad: 기울기의 반대 방향으로 x를 업데이트.

def function_2(x):
    return x[0]**2 + x[1]**2

• 테스트용 함수.

init_x = np.array([-3.0, 4.0])

lr = 0.1
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, \
                                step_num=step_num)

• init_x: 초기 위치. (-3.0, 4.0)
• lr = 0.1: 학습률 0.1. 경사하강법이 한 번에 기울기의 10%만큼 이동하도록 한다.
• step_num = 20: 경사하강법을 20번 반복한다.
• x_history: 학습 과정에서 x의 변화를 기록한다.

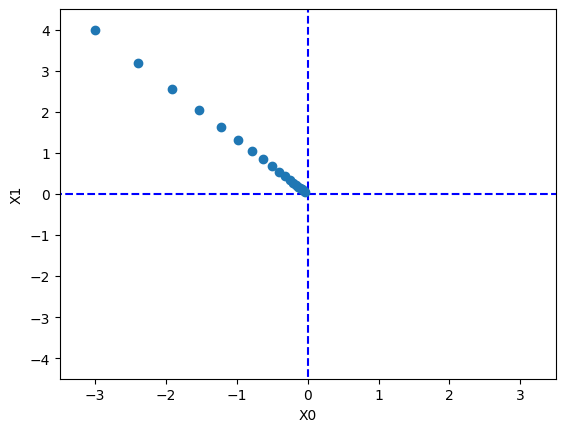
plt.plot([-5, 5], [0, 0], '--b')
plt.plot([0,0], [-5, 5], '--b')
plt.plot(x_history[:, 0], x_history[:,1], 'o')

plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel('X0')
plt.ylabel('X1')
plt.show()

• x_history[:, 0]: 각 학습 단계에서 x0 값.
• x_history[:, 1]: 각 학습 단계에서 x1 값.
• x0-x1 평면에서 학습 과정 동안 어떻게 x가 움직였는지 보여준다. 이는 경사하강법이 (-3.0, 4.0)에서 시작해 (0, 0)으로 수렴하는 과정을 나타낸다.
  

신경망에서의 기울기

class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2, 3) # 정규분포로 초기화

• 신경망의 가중치를 초기화하는 역할.
• self.W: 가중치 매트릭스. 2*3 크기의 행렬. 이 행렬은 정규분포를 따르는 난수로 초기화된다.
  - 2개의 입력값을 받고 3개의 출력값을 내놓는 네트워크.
  • np.random.randn(2, 3): 평균이 0이고 표준편차가 1인 정규분포에서 무작위로 값을 뽑아 2*3 행렬로 만든다.

    def predict(self, x):
        return np.dot(x, self.W)

• predict: 입력 데이터 x를 받아 가중치와의 행렬 곱을 계산하여 출력값을 반환.
  - np.dot(x, self.W): x와 가중치 W를 곱해 선형 결합을 수행.
  • x는 1*2 크기의 벡터이고, W는 2*3 크기의 행렬이므로 결과는 1*3 크기의 벡터가 된다. 이 벡터는 각 클래스에 대한 점수(score) 를 나타낸다.

    def loss(self, x, t):
        z = self.predict(x)
        y = softmax(z)
        loss = cross_entropy_error(y, t)

        return loss 

• 주어진 입력 데이터 x에 대해 손실(loss)를 계산하는 함수.
• z = self.predict(x): 입력 데이터를 기반으로 예측값 z를 계산한다. 이 값은 각 클래스에 대한 점수(score)를 의미한다.
• y = softmax(z): 소프트맥스(softmax) 함수를 사용하여 예측값을 확률로 변환한다. 소프트맥스 함수는 점수들을 확률 분포로 변환하는데 이 확률은 각 클래스에 속할 확률을 의미한다.
• loss = cross_entropy_error(y, t): 교차 엔트로피 손실 함수를 사용해 예측된 확률값 y와 실제 레이블 t 사이의 차이를 계산한다. 손실 값이 작을수록 예측이 정확하다는 뜻.

2층 신경망 클래스 구현

클래스 초기화

class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
            # 가중치 초기화
            self.params = {}
            self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
            self.params['b1'] = np.zeros(hidden_size)
            self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
            self.params['b2'] = np.zeros(output_size)

• input_size: 입력층의 노드 수(특성 수).
• hidden_size: 은닉층의 노드 수.
• output_size: 출력층의 노드 수(클래스 수).
• 가중치는 정규분포를 따른 무작위 값으로 초기화되며, weight_init_std에 의해 크기가 조정된다.

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']

        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        return y

• 순전파.

    def loss(self, x, t):
        y = self.predict(x)

        return cross_entropy_error(y, t)

• 손실 함수.

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

• 정확도 계산 함수.

    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

• 수치미분을 사용한 기울기 계산 함수.

미니배치 학습

import numpy as np
from dataset.mnist import load_mnist

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

• 데이터 로드.

train_loss_list = []

# 하이퍼파라미터
iters_num = 5 # 반복 횟수를 적절히 설정
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1

• iters_num: 경사하강법을 반복할 횟수. 이 값이 클수록 더 많은 반복을 통해 학습이 진행된다.
• train_size: 학습 데이터의 총 크기.
• batch_size: 각 학습 단계에서 사용할 미니배치의 크기.
• learning_rate: 학습률. 가중치가 기울기를 따라 업데이트되는 정도를 조절한다.

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

• 네트워크 초기화.

for i in range(iters_num):
    # 미니배치 획득
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

• np.random.choice: train_size에서 batch_size 만큼의 인덱스를 무작위로 선택해 x_batch와 t_batch에 할당.

    # 기울기 계산
    grad = network.numerical_gradient(x_batch, t_batch)

    # 매개변수 갱신
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    # 학습 경과 기록
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

print('Train Loss: ', train_loss_list)