열여덟번째 수업 | 통계기반 데이터 활용

강명호 강사님

개요

통계와 데이터

통계는 데이터를 수집하고 분석하는 방법을 통해 우리로 다양한 현상을 이해할 수 있게 도와준다.

• 기술 통계: 데이터를 요약하고, 평균, 중간값, 분산과 같은 기초적 수치를 계산한다.
• 추론 통계: 주어진 데이터를 바탕으로 예측을 하고, 결론을 도출한다.

머신러닝

머신러닝은 사람이 명령을 내리던 전통적 프로그램과 달리 데이터를 통해 규칙을 학습, 새로운 데이터를 바탕으로 예측하는 기술이다.
1. 문제 정의: 어떤 문제를 해결할 것인지 명확히 설정
2. 데이터 준비: 필요한 데이터를 수집하고, 분석하기 쉽게 가공
3. 모델링: 데이터에서 규칙을 찾는 모델(알고리즘)을 만듦
4. 모델 평가: 모델이 얼마나 정확한지 평가하고 필요하면 수정

Azure Machine Learning

Azure Machine Learning은 클라우드 기반 머신러닝 플랫폼으로, 데이터 준비부터 모델링, 평가, 배포까지 할 수 있다.
1. 데이터 등록: 데이터를 시스템에 올려서 분석할 수 있게 준비
2. 모델링: 데이터를 분석하고 학습하는 알고리즘을 만들고 훈련시킴
3. 배포: 완성된 모델을 실제 환경에 적용하여 새로운 데이터를 예측하는데 사용

통계 기초

모집단과 표본

• 모집단(Population): 조사하려는 전체 집단
• 표본(Sample): 모집단 전체를 조사하는 것은 어렵기 때문에 일부만 뽑아서 조사를 하는데, 그 일부를 표본이라고 함

중심경향성

데이터의 중심을 찾는 방법.

• 평균(Mean): 모든 값을 더해서 개수로 나눈 값
• 중앙값(Median): 데이터를 크기 순서대로 나열했을 때 중간에 위치한 값
• 최빈값(Mode): 데이터 중에서 가장 자주 나오는 값

산포도

데이터가 얼마나 흩어져 있는지 나타내는 것.

• 범위(Range): 가장 큰 값과 가장 작은 값의 차이
• 분산(Variance): 데이터 값들이 평균에서 얼마나 떨어져 있는지를 나타냄. 평균과 얼마나 차이가 나는지를 제곱하여 그 평균을 구하는 방식
• 표준편차(Standard Deviation): 분산의 제곱근으로, 데이터가 얼마나 퍼져 있는지 쉽게 이해할 수 있게 돕는 지표

확률

어떤 사건이 일어날 가능성을 수치로 나타내는 것으로, 0에서 1사이의 값을 가진다. 0은 절대 일어나지 않는 것, 1은 반드시 일어나는 것.

• 확률변수(Random Variable): 어떤 결과가 나올지 확률적으로 나타내는 변수

확률분포

확률변수가 가질 수 있는 값들과 그 값들이 발생할 확률을 나타내는 함수를 말한다.

• 이산 확률 분포: 나올 수 있는 값이 셀 수 있는 경우
• 연속 확률 분포: 값이 연속적인 경우

추정과 가설검정

• 추정(Estimation): 표본을 통해 모집단에 대한 정보를 추정하는 것
• 가설검정(Hypothesis Testing): 어떤 가설이 맞는지 아닌지를 통계적으로 검증하는 과정

상관분석

두 변수 간의 관계를 알아보는 것

• 양의 상관관계: 두 변수가 같이 커지는 경우
• 음의 상관관계: 한 변수가 커질수록 다른 변수가 작아지는 경우

데이터 시각화

데이터 시각화는 데이터를 그래프나 차트 같은 시각적 형태로 표현해서 데이터를 쉽게 이해하고 패턴이나 관계를 파악할 수 있도록 도와주는 기법

데이터 시각화의 필요성

• 데이터 패턴 파악: 데이터를 시각화하면 복잡한 패턴이나 트렌드를 쉽게 파악할 수 있다.
• 데이터 간의 관계 분석: 산점도(Scatter Plot) 를 사용하면 두 변수 사이의 상관 관계를 시각적으로 분석할 수 있다.
• 의사소통: 복잡한 데이터 분석 결과를 그래프로 표현하면 다른 사람에게 설명할 때 더 효과적으로 전달할 수 있다.

데이터 시각화의 주요 기법

막대 그래프(Bar chart)

막대 그래프는 범주형 데이터를 표현하는 데 많이 사용된다. 각 범주에 해당하는 값을 막대의 길이로 나타내서 쉽게 비교할 수 있다.

히스토그램(Histogram)

히스토그램은 데이터를 구간으로 나눠서 각 구간에 속하는 데이터의 빈도를 막대 그래프로 나타내는 기법이다. 데이터의 분포를 파악할 때 유용하다.

선 그래프(Line Graph)

선 그래프는 데이터를 시간 또는 순서에 따라 연결하여 변화를 보여주는 그래프로, 시간이 지나면서 데이터가 어떻게 변화하는지 볼 때 많이 사용된다.

파이 차트(Pie Chart)

파이 차트는 하나의 전체를 구성하는 각 부분의 비율을 나타낼 때 사용된다. 원을 여러 개의 조각으로 나눠서 각 조각이 전체에서 차지하는 비율을 보여준다.

산점도(Scatter Plot)

산점도는 두 변수 간의 관계를 나타내는 그래프로, 데이터를 좌표평면에 점으로 표시해서 두 변수 간의 상관 관계를 파악할 수 있다.

박스 플롯(Box Plot)

박스 플롯은 데이터의 분포를 간단하게 요약해 보여주는 그래프이다. 데이터의 중앙값, 사분위수, 최솟값, 최댓값 등을 한 번에 파악할 수 있다. 이 그래프는 데이터에 이상치가 있는지 확인할 때 특히 유용하다.

확률 분포

이산 확률 분포

베르누이 분포 (Bernoulli Distribution)

• 정의: 성공 또는 실패, 두 가지 결과만 가능한 실험에 대한 확률 분포. 하나의 시행에서 성공하면 1, 실패하면 0의 값을 가짐.
• 확률 질량 함수(PMF): $P(X = x) = \begin{cases} p, & \text{if } x = 1 \\ 1 - p, & \text{if } x = 0 \end{cases}$
• 여기서 p는 성공할 확률

이항 분포 (binomial Distribution)

• 정의: 이항 분포는 베르누이 시행을 여러 번 반복한 결과에 대한 확률 분포이다. 즉, n번의 독립적인 시행에서 성공한 횟수를 나타낸다.
• 확률 질량 함수(PMF):
  $P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k}$
• 여기서 $\binom{n}{k}$는 이항계수, p는 성공할 확률, k는 성공 횟수

포아송 분포 (Poisson Distribution)

• 정의: 포아송 분포는 단위 시간 또는 단위 공간에서 특정 사건이 발생하는 횟수에 대한 분포이다. 주로 드문 사건이 발생하는 빈도를 설명하는 데 사용된다.
• 확률 질량 함수(PMF):
  $P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}$
• 여기서 $lambda$는 단위 시간 당 사건이 발생하는 평균 횟수이다.

연속 확률 분포 (Continuous Probability Distribution)

정규 분포 (Normal Distribution)

• 정의: 정규 분포는 자연 현상에서 가장 많이 나타나는 분포로 종 모양의 대칭 분포를 가지고 있다. 평균을 중심으로 대칭적인 형태를 가지며, 데이터가 평균 주위에 모여 있는 경향을 보여준다.
• 확률 밀도 함수(PDF):
  $f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}$
• 여기서 $\mu$는 평균, $\sigma$는 표준편차를 의미한다.

지수 분포 (Exponential Distribution)

• 정의: 지수 분포는 사건 간의 시간 간격을 설명하는 분포로 주로 포아송 분포에서 사건이 발생하는 시간 간격을 모델링할 때 사용된다.
• 확률 밀도 함수(PDF):
  $f(x) = \lambda e^{-\lambda x}, \quad x \geq 0$
• 여기서 $\lambda$는 사건 발생률을 나타낸다.

카이제곱 분포 (Chi-Square Distribution)

• 정의: 카이제곱 분포는 정규 분포를 따르는 독립적인 변수들의 제곱합으로 이루어진 분포이다. 주로 모집단의 분산을 추정하거나 적합도 검정, 독립성 검정에서 사용된다.
• 확률 밀도 함수(PDF):
  $f(x) = \frac{1}{2^{k/2} \Gamma(k/2)} x^{k/2-1} e^{-x/2}, \quad x \geq 0$
• 여기서 k는 자유도, $\Gamma$는 감마 함수이다.

가설 검정 (Hypothesis Testing)

가설 검정은 표본 데이터를 통해 모집단에 대한 가설이 맞는지 아닌지를 통계적으로 평가하는 과정이다. 기본적으로 두 가지 가설을 세우고, 이를 바탕으로 통계적 결론을 내린다.

가설 검정의 주요 단계

가설 설정

• 귀무 가설 (Null Hypothesis, $H_0$): 보통 '차이가 없다' 또는 '효과가 없다'는 주장을 의미한다. 검정의 기준이 되는 가설이다.
• 대립 가설 (Alternative Hypothesis, $H_1$): 귀무가설에 반대되는 가설로, '차이가 있다' 또는 '효과가 있다'는 주장을 의미한다. 이를 증명하고자 하는 가설이다.

유의수준 (Significance Level, $\alpha$) 설정

유의수준은 귀무가설을 기각할 때 오류를 허용하는 확률이다. 일반적으로 $\alpha$는 0.05 또는 0.01로 설정한다. $\alpha = 0.05$라면, 5%의 확률로 귀무가설이 참인데도 불구하고 이를 기각할 가능성을 허용하는 것이다.

검정 통계량 계산

표본 데이터를 이용해 검정 통계량을 계산한다. 이때 사용하는 검정 방법에 따라 t-검정, 카이제곱 검정, 분산 분석(ANOVA) 등이 있다.

기각 여부 결정

계산된 검정 통계량으로부터 p-값(P-value)을 계산한다. p-값은 귀무가설이 맞다는 가정하에 관찰된 결과가 발생할 확률을 나타낸다.

• p-값이 설정한 유의수준 a보다 작으면 귀무가설을 기각한다.(즉, 대립가설이 맞다고 판단)
• p-값이 설정한 유의수준보다 크면 귀무가설을 채택한다.(즉, 차이가 없다고 판단)

가설 검정의 오류

• 1종 오류 (Type I Error): 귀무가설이 참인데도 불구하고 이를 기각하는 오류. 즉, 실제로 차이가 없는데 차이가 있다고 잘못 결론 내리는 경우이다. 이는 잘못된 긍정이라고도 한다.
• 2종 오류 (Type II Error): 대립가설이 참인데도 불구하고 귀무가설을 기각하지 않는 오류. 즉, 실제로 차이가 있는데도 차이가 없다고 결론을 내리는 경우이다. 이는 잘못된 부정이라고 한다.

가설 검정 방법

t-검정 (t-test)

두 그룹의 평균을 비교할 때 사용한다.

• 단일 표본 t-검정: 하나의 표본과 특정 값을 비교할 때.
• 독립 표본 t-검정: 두 개의 독립된 그룹의 평균을 비교할 때.
• 대응 표본 t-검정: 동일한 그룹의 두 상황을 비교할 때.

카이제곱 검정 (Chi-square test)

범주형 데이터에서 두 변수 간의 독립성을 검정하거나 적합도를 검정할 때 사용.

• 적합도 검정 (Goodness of Fit Test): 관찰된 데이터가 기대되는 분포와 일치하는지 검정.
• 독립성 검정 (Test of Independence): 두 변수 간의 독립성을 검정.

분산 분석 (ANOVA, Analaysis of Variance)

세 개 이상의 그룹의 평균을 비교할 때 사용.

• 일원 분산 분석 (One-way ANOVA): 하나의 요인에 대한 그룹 간의 평균 차이를 검정.
• 이원 분산 분석 (Two-way ANOVA): 두 개의 요인에 대한 그룹 간의 평균 차이를 검정.

상관 분석 (Correlation Analysis)

상관 분석은 두 변수 간의 관계를 평가하는 통계 기법이다. 상관 분석을 통해 한 변수가 변할 때 다른 변수가 어떻게 변하는지 파악할 수 있다.

상관 계수 (Correlation Coefficient)

상관계수는 두 변수 간의 관계의 강도와 방향을 나타내는 값이다. 상관계수의 값은 -1에서 1사이의 값을 가진다.

• $r = 1$: 두 변수 간에 완전한 양의 상관관계가 있음
• $r = -1$: 두 변수 간에 완전한 음의 상관관계가 있음
• $r = 0$: 두 변수 간에 상관관계가 없음

상관 분석의 종류

피어슨 상관계수 (Pearson Correlation Coefficient)

• 두 연속형 변수 간의 선형 관계를 측정한다.
• 계산 방법: 두 변수의 공분산을 각 변수의 표준편차로 나누어 계산
  $r = \frac{\sum (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum (X_i - \bar{X})^2} \sqrt{\sum (Y_i - \bar{Y})^2}}$

스피어만 상관계수 (Spearman's Rank Correlation Coefficient)

• 두 순위형 변수 간의 상관관계를 측정하며, 비선형 관계가 있을 때에도 사용할 수 있다.
• 각 변수의 값을 순위로 변환한 후, 그 순위 간의 상관관계를 계산한다.
  $r_8 = 1 - \frac{6 \sum d^2_i}{n(n^2-1)}$
• 여기서 $d_i$는 각 데이터 점의 순위 차이, n은 데이터의 개수이다.

켄달의 타우 (Kendall's Tau)

• 작은 데이터셋에서 두 변수의 순서 간 상관성을 측정하는 방법이다. 데이터 쌍 간의 일치와 불일치를 비교하여 상관관계를 계산한다.

상관 관계의 해석

• 강한 상관관계: 상관계수의 절댓값이 0.7 이상일 때, 두 변수는 강한 상관관계를 가진다.
• 중간 상관관계: 상관계수의 절댓값이 0.3~0.7일 때, 중간 정도의 상관관계가 있다.
• 약한 상관관계: 상관계수의 절댓값이 0.3 미만일 때, 약한 상관관계가 있다.

머신러닝

머신러닝 개념

• 인공지능(AI): 인간의 지적 능력을 컴퓨터로 구현한 기술.
• 머신러닝(ML): AI의 한 분야로, 컴퓨터가 명시적인 지시 없이도 데이터를 보고 스스로 패턴을 찾아 작업을 수행하는 알고리즘. 즉, 데이터를 통해 학습하는 것.
• 딥러닝(DL): 머신러닝의 한 종류로, 뇌의 신경망을 모방한 인공 신경망을 사용하여 더 복잡한 문제를 해결하는 방식.

머신러닝의 목적

데이터에 숨어있는 규칙을 찾고 이를 바탕으로 새로운 데이터를 예측하는 것

머신러닝 종류

지도학습 (Supervised Learning)

지도학습은 정답이 있는 데이터로부터 학습하는 방식이다. 즉, 이미 알고 있는 입력 데이터와 그에 해당하는 정답을 바탕으로 모델을 학습시키고, 새로운 데이터가 들어왔을 때 올바른 정답을 예측하는 것이다.

• 회귀(Regression): 수치 값을 예측하는 방법
• 분류(Classification): 범주를 예측하는 방법

비지도학습(Unsupervised Learning)

비지도학습은 정답이 없는 데이터를 학습하는 방식이다. 즉, 정답이나 레이블이 없는 데이터를 기반으로 패턴을 찾거나 데이터를 그룹화하는 방법이다. 비지도학습의 목표는 데이터가 가지고 있는 숨겨진 구조를 발견하는 것이다.

• 군집(Clustering): 비슷한 데이터를 하나의 그룹으로 묶는 방법

머신러닝 용어

데이터 세트(Data Set)

머신러닝 모델이 학습할 수 있는 모든 데이터

데이터 샘플(Sample)

데이터 세트에서 개별적으로 추출한 하나의 데이터

특성(Feature)

데이터의 개별 속성. 머신러닝에서는 이 특성을 인풋으로 사용하여 모델을 학습한다.

레이블(Label)

지도학습에서 정답 역할을 하는 값. 모델이 예측하려는 목표 값이며, 분류나 회귀 모델에서 중요한 역할을 한다.

범주(Class)

분류 문제에서 예측할 수 있는 카테고리 또는 결과 유형

학습 데이터(Training Data)

모델을 학습시키기 위해 사용되는 데이터. 모델이 규칙을 학습할 수 있도록 도와줌.

테스트 데이터(Test Data)

학습된 모델이 얼마나 잘 예측하는지 확인하기 위해 사용되는 데이터. 학습 과정에서 사용되지 않으며, 모델의 성능을 평가하는 데 사용됨.

입력(Input)

모델이 학습하거나 예측을 위해 받는 데이터의 특성

타겟(Target)

모델이 예측하고자 하는 정답값. 레이블과 동일한 개념으로, 주로 지도학습에서 사용됨

오차 행렬(Confusion Matrix)

이진 분류 모델에서 예측 성능을 평가하기 위해 사용하는 행렬이다. 모델이 올바르게 예측한 것과 잘못 예측한 것의 수를 확인할 수 있다.

• True Positive (TP): 실제 값도 긍정이고, 예측도 긍정인 경우
• False Positive (FP): 실제 값은 부정인데, 예측은 긍정으로 잘못된 경우
• True Negative (TN): 실제 값도 부정이고, 예측도 부정인 경우
• False Negative (FN): 실제 값은 긍정인데, 예측은 부정으로 잘못된 경우

정확도(Accuracy)

• 정의: 모델이 올바르게 예측한 비율. 전체 예측 중 맞춘 비율을 계산.
• 계산: $\frac{TP + TN}{TP + TN + FP + FN}$

정밀도(Precision)

• 정의: 모델이 긍정으로 예측한 값 중 실제로 맞은 값의 비율. FP를 줄이는 데 중요한 역할을 한다.
• 계산: $\frac{TP}{TP + FP}$

재현율(Recall)

• 정의: 실제 긍정인 값 중 모델이 긍정으로 맞춘 비율. FN을 줄이는 데 중요한 역할을 한다.
• 계산: $\frac{TP}{TP + FN}

과대적합(Overfitting)

모델이 학습 데이터에 너무 맞춰져서 새로운 데이터에 대한 예측 성능이 떨어지는 경우. 이는 모델이 학습 데이터의 노이즈까지 학습해버려 발생한다.

하이퍼파라미터(Hyperparameter)

모델이 학습하는 동안 변경되지 않고 사용자가 직접 설정하는 매개변수.

데이터 수집 및 준비

로켓 발사 여부를 예측하기 위해 NASA 등 기관의 기상 데이터를 수집한다.

분류 모델 설명

로켓 발사 여부를 예측하기 위해서는 분류 모델이 필요하다. 분류 모델은 데이터를 카테고리로 나누어 예측하는 모델이다.

• 이진 분류(Binary Classification): 결과가 두 가지로 나뉘는 경우
• 다중 클래스 분류(Multi-class Classification): 결과가 여러 가지로 나뉘는 경우

알고리즘 선택

분류 모델을 만들기 위해 다양한 알고리즘을 사용할 수 있다.

• 의사 결정 나무: 데이터를 분류하기 위한 일련의 질문을 나무 구조로 만들어 최적의 결정을 내린다.
• 랜덤 포레스트: 여러 개의 의사 결정 나무를 결합해 정확도를 높이는 방법.

모델 학습

모델 학습 단계는 데이터를 사용해 알고리즘이 규칙을 찾는 과정으로, 이 때 데이터를 학습 데이터(Training Data) 와 테스트 데이터(Test Data) 로 나누어 학습한다. 학습 데이터는 모델이 규칙을 학습하는 데 사용되고, 테스트 데이터는 학습이 끝난 후 모델이 얼마나 잘 예측하는지 평가하는 데 사용된다.

모델 평가

• 정확도(Accuracy): 예측이 실제 값과 얼마나 일치하는지 평가하는 지표
• 정밀도(Precision): 모델이 예측한 값 중 실제로 맞는 비율
• 재현율(Recall): 실제 맞는 값 중 모델이 예측한 비율

의사결정나무

의사결정나무는 데이터를 기반으로 질문을 만들어 나가며, 이를 통해 분류 또는 예측을 한다. 이 알고리즘은 데이터를 분리할 수 있는 규칙을 찾아 가장 잘 분류할 수 있는 질문을 하나씩 선택해 나간다.

구조와 용어

• 노드(Node): 데이터를 분류하기 위한 질문 또는 테스트 조건이 들어가는 부분
  - 루트 노드(Root Node): 가장 위에 위치한 첫 번째 질문
  • 리프 노드(Leaf Node): 더 이상 질문이 필요 없을 때 최종 결과(분류)가 나오는 노드
  • 부모 노드(Parent Node) 와 자식 노드(Child Node): 부모 노드는 하나 이상의 자식 노드를 가지고 있으며, 각 질문이 새로운 질문으로 이어지는 방식. (Like 스무고개!)
• 가지(Branch): 각 질문에 대한 결과로 연결된 노드. 가지는 질문에 대한 다양한 대답에 따라 분리된 노드들을 연결한다.

의사결정 나무의 작동 원리

데이터 분할

의사 결정 나무는 데이터를 반복적으로 분할하는 방식으로 동작한다. 각 분할은 하나의 질문에 해당하며, 질문을 통해 데이터가 분리된다.

질문의 선택

각 질문은 불순도를 최소화하는 방향으로 선택된다. 불순도(Impurity) 는 데이터가 얼마나 섞여 있는지를 나타내며 동일한 범주의 데이터가 많이 모일수록 불순도가 낮아진다.

• 지니 불순도(Gini Impurity) : 의사결정 나무에서 주로 사용되는 불순도 지표. 데이터를 나눌 때, 얼마나 순수하게 분류되는지를 나타낸다.
  $Gini(T) = 1 - \sum (P_i)^2$
• 여기서 $P_i$는 각 범주(클래스)의 비율이다.

의사결정 나무에서 불순도를 줄이는 과정

각 노드는 데이터를 가능한 순수하게나누기 위해 여러 질문(테스트 조건)을 시도한다. 각 분할에서 불순도가 가장 많이 줄어드는 질문을 선택한다.

의사결정 나무의 과대적합(Overfitting) 문제

의사결정 나무는 데이터를 너무 세밀하게 분류하다 보면, 과대적합(overfitting) 문제가 발생할 수 있다. 즉, 모델이 학습 데이터에 지나치게 맞추어져 새로운 데이터에 대한 예측 성능이 떨어지게 된다.

해결 방법

나무의 깊이를 제한하거나 가지치기(Pruning) 기술을 사용하여 불필요한 분할을 제거함으로써 과대적합을 방지할 수 있다.

예측 확률

의사결정 나무는 특정 범주에 속할 확률도 예측할 수 있다.

랜덤 포레스트(Random Forest)와의 차이점

의사결정 나무는 하나의 나무를 사용해 예측을 하지만 랜덤 포레스트는 여러 개의 의사결정 나무를 사용해 앙상블(Ensemble) 기법으로 예측을 강화한다. 여러 나무의 예측을 모아서 더 강력한 예측 결과를 도출할 수 있다.

로켓 발사 예측 모델 작성 실습

Azure 환경 준비

이건 이제 금방 하니까 패스
1. Azure 가입 or 로그인
2. 리소스 그룹 생성
3. 머신러닝 리소스 생성

데이터 수집 및 이해

데이터 세트 등록

실습에 사용할 데이터 파일을 Azure 머신러닝 스튜디오에 업로드

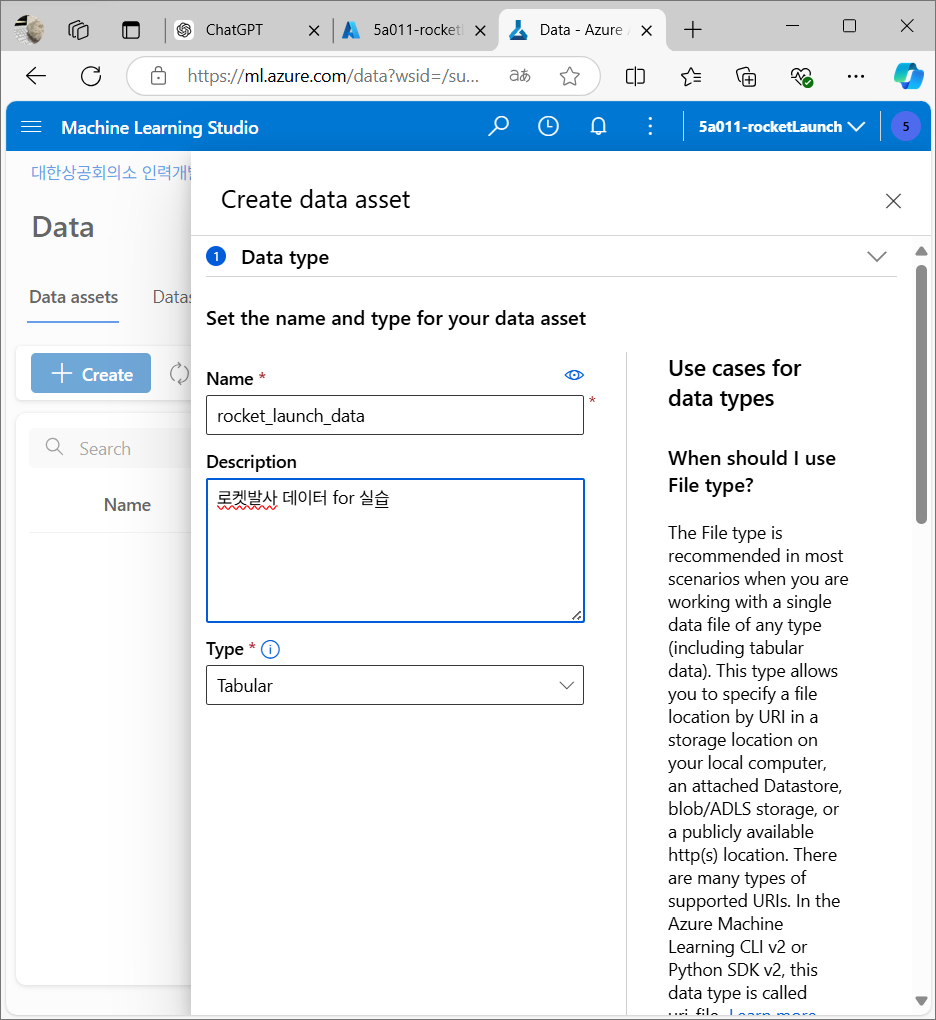
데이터 미리보기

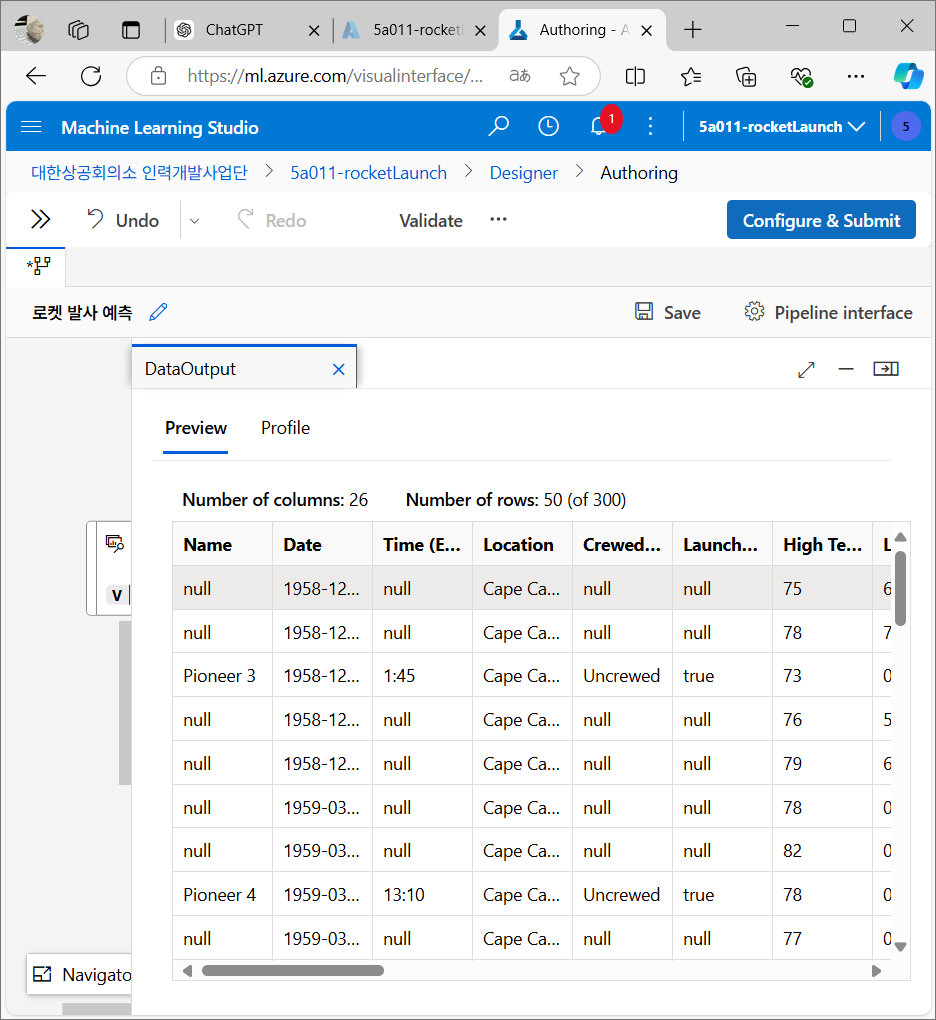
데이터 준비

필요한 특성 선택

모델 학습에 필요한 주요 컬럼을 선택하고 불필요한 컬럼 제거

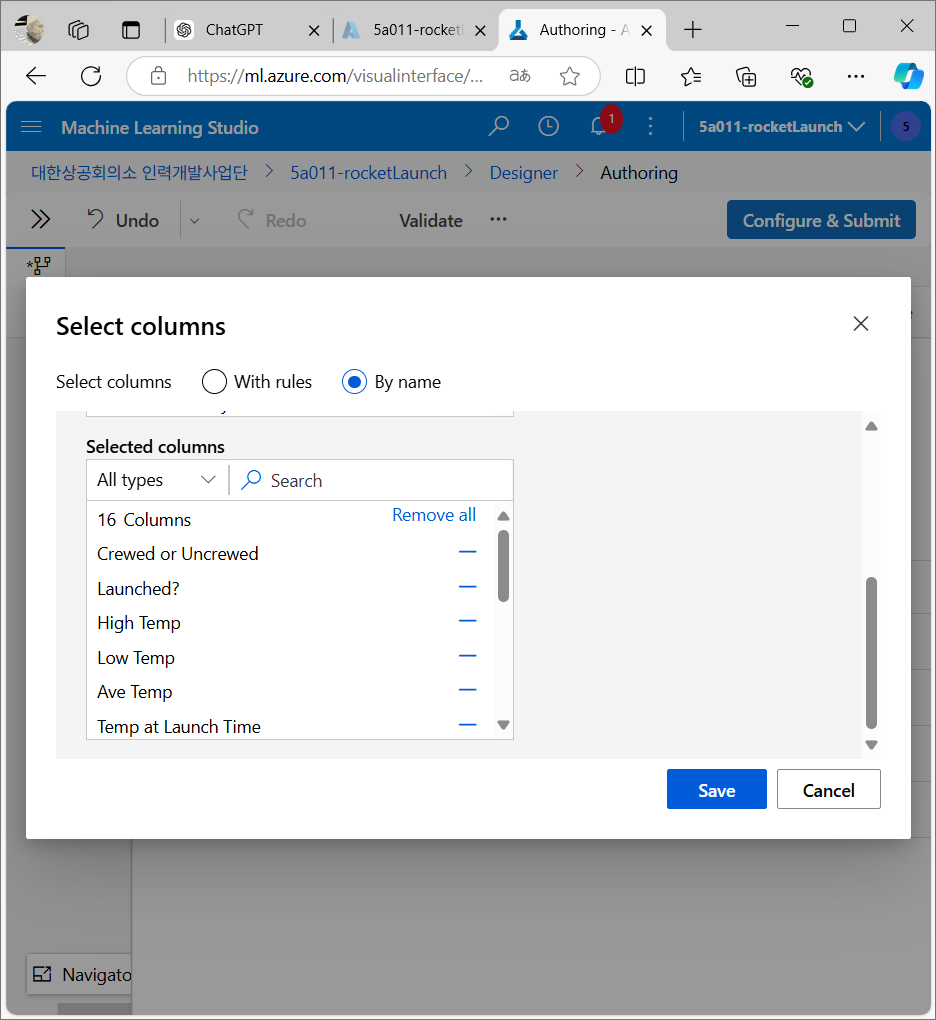
누락값 처리

데이터에 누락된 값이 있을 경우 기본값을 설정하여 처리

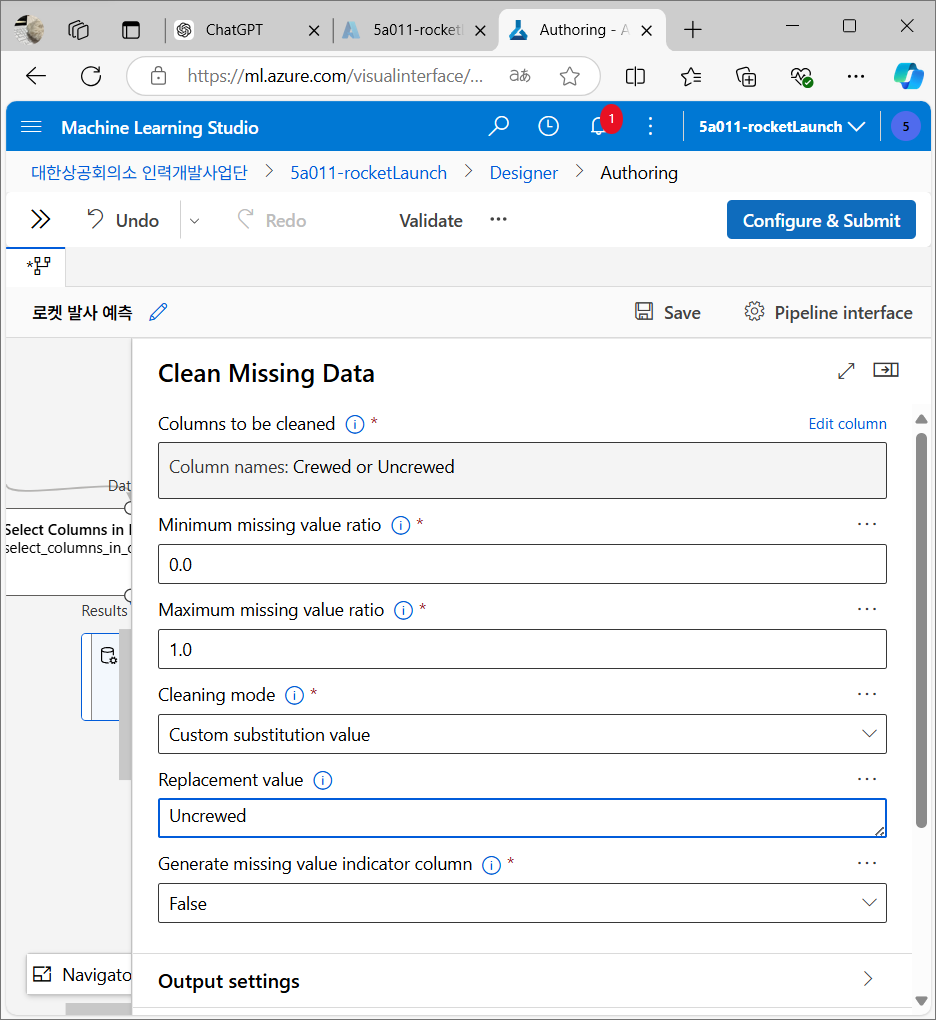
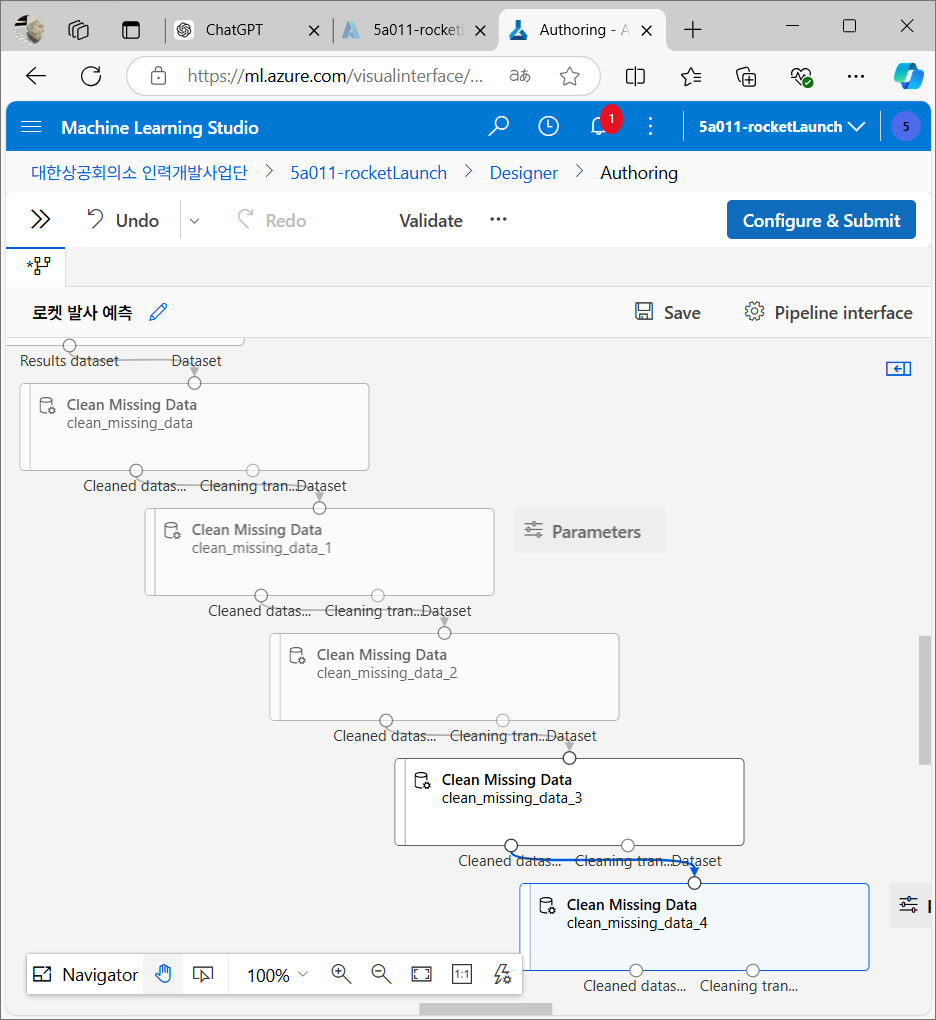
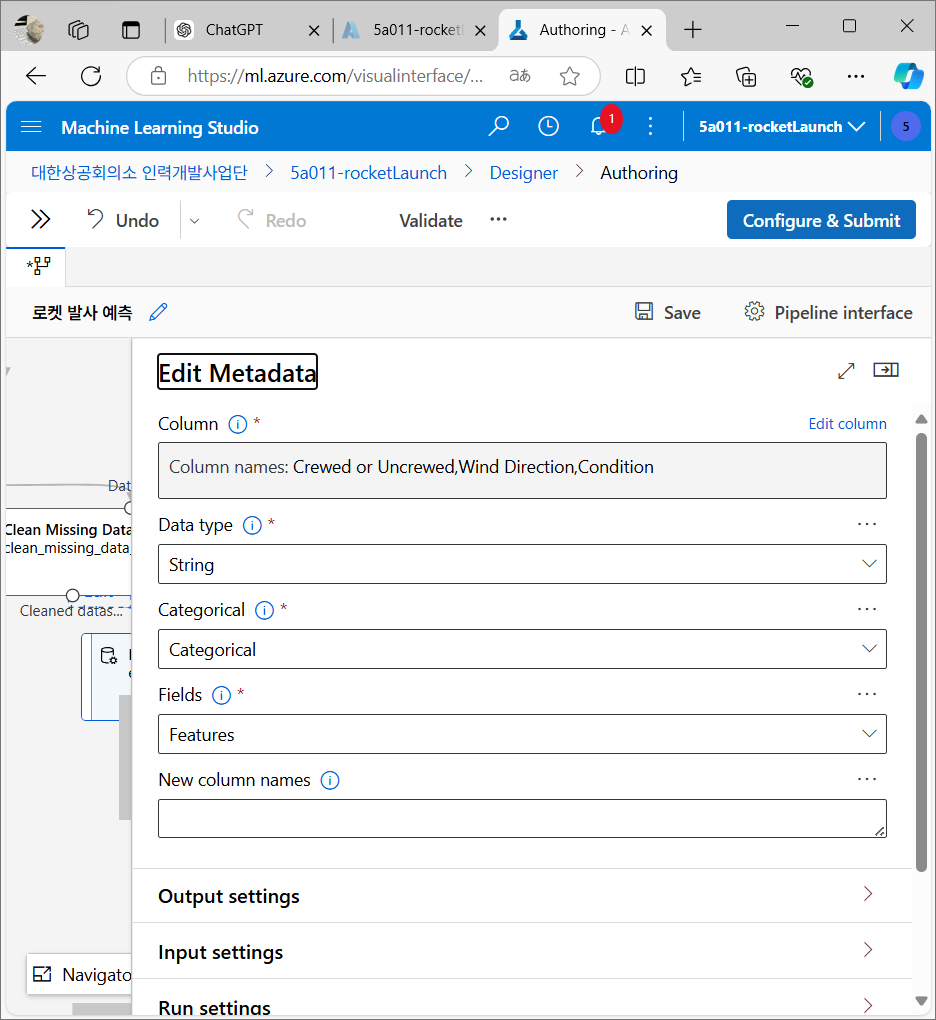
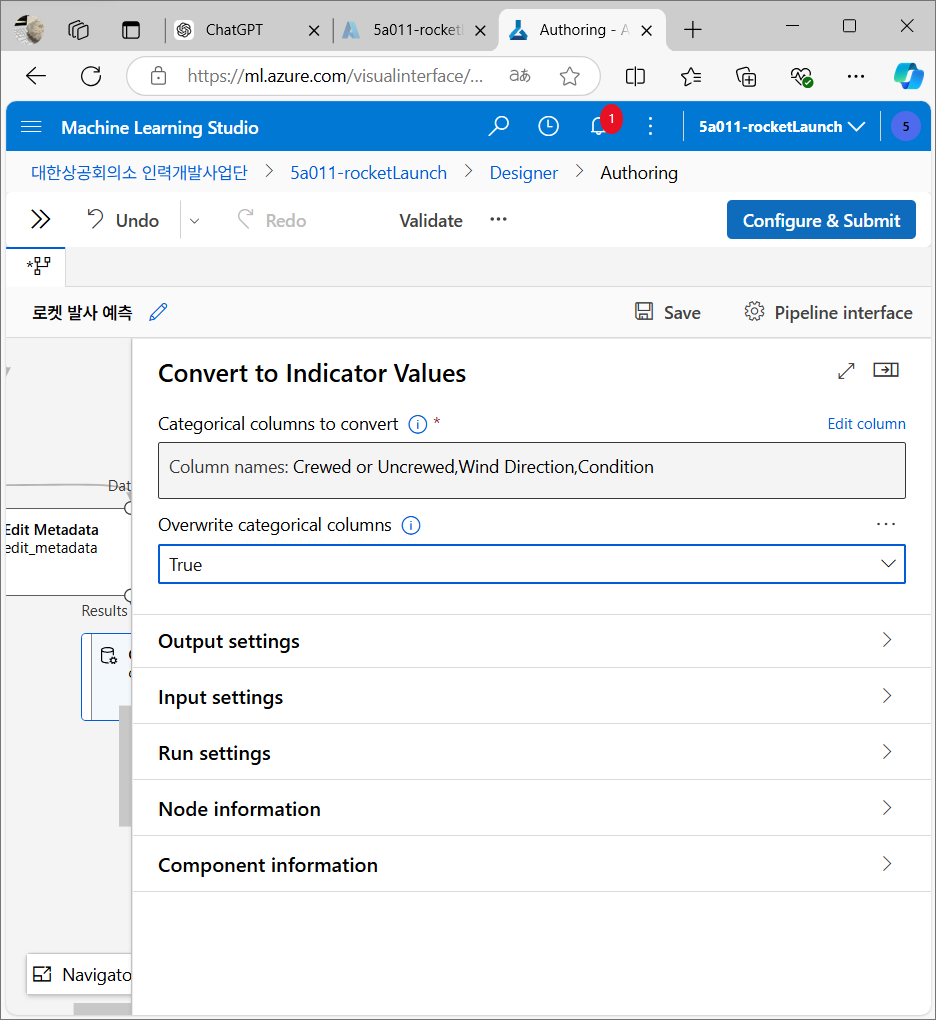
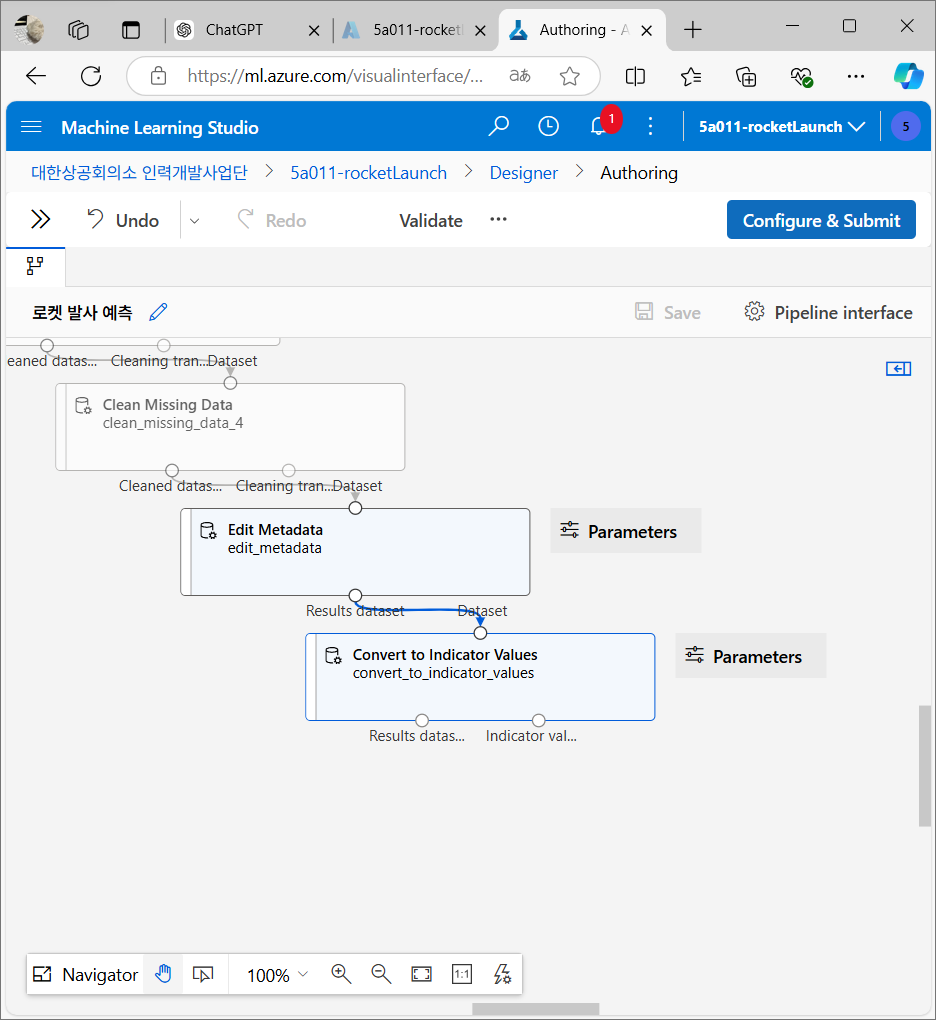
데이터 변환

텍스트 데이터를 범주형 데이터로 변환 후 숫자로 변환해 머신 러닝 모델이 사용할 수 있도록 만든다.

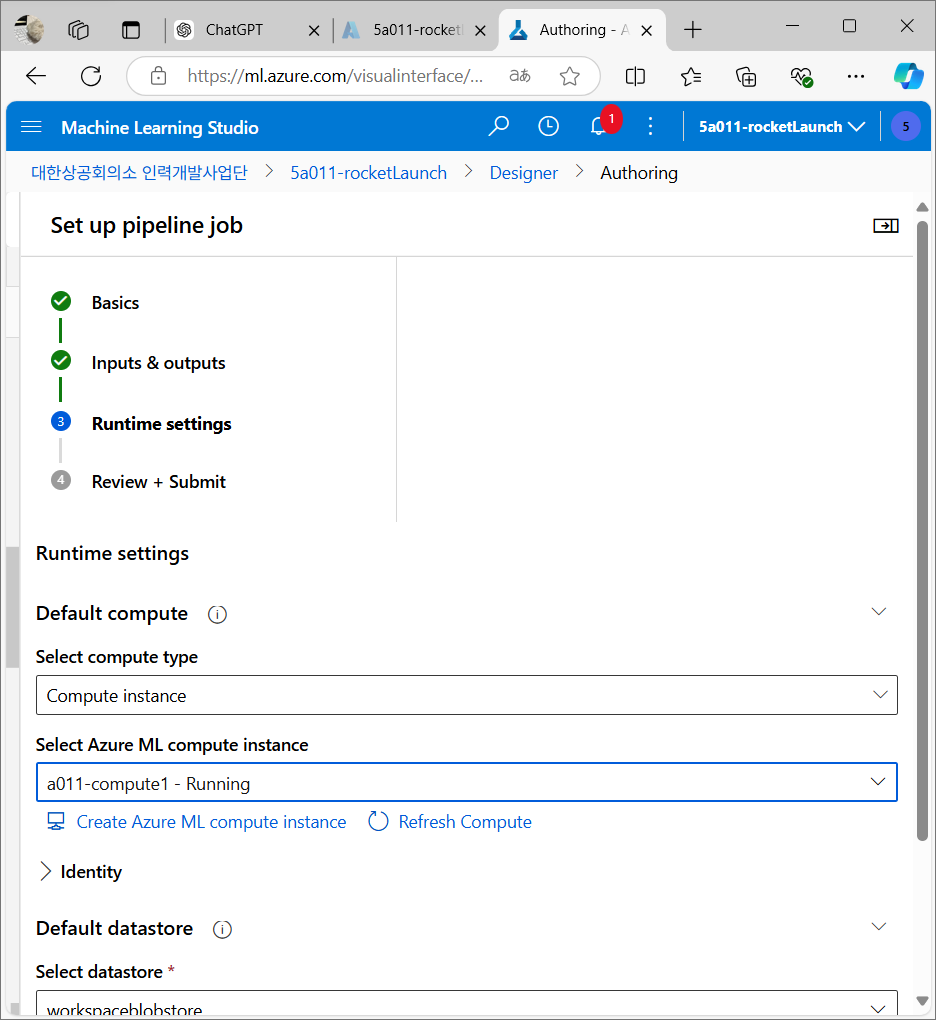
컴퓨트 대상 설정

Azure에서 머신러닝 작업을 수행할 가상 머신 설정

Personal Insight

강명호 강사님은 팀즈도 워낙 능숙하게 활용하시고, 준비해주시는 PPT 자료도 상세하고 설명이 잘 되어 있어서 수업을 따라가기에 너무 좋다. 소통도 굉장히 원활하게 이루어져서 강명호 강사님 수업 들을 때마다 즐겁다. 쉬는 시간도 마치 다음 수업을 기대하게 하는 to be continued 10분 후에 공개됩니다 광고시간처럼 느껴진달까. 주말에 잘 쉬고 나서 컨디션이 회복된 덕분에 오늘 수업에 더 잘 집중할 수 있었던 것 같다. '휴식의 중요성'을 새삼 깨닫는 날.
파이썬 공부하면서 ipynb 파일로만 작업하던 것을 Azure 머신러닝 스튜디오에서 실행해보니 훨씬 간편하고 직관적이어서 재미있고, 파이썬으로 작업했다면 어떻게 코드를 작성했을까, 생각하고 비교해보는 과정도 흥미롭다. 학습 동기부여 뿜뿜. 내일 수업도 기대가 된다. 5기, 16반 파이팅!