열아홉번째 수업 | 로켓 발사 예측 실습 마무리 | 자전거 렌탈 수요 예측 모델 구현 | 회귀 모델 | 프로야구 선수 능력 측정 모델 구현 | 군집 모델

강명호 강사님

로켓 발사 예측 실습

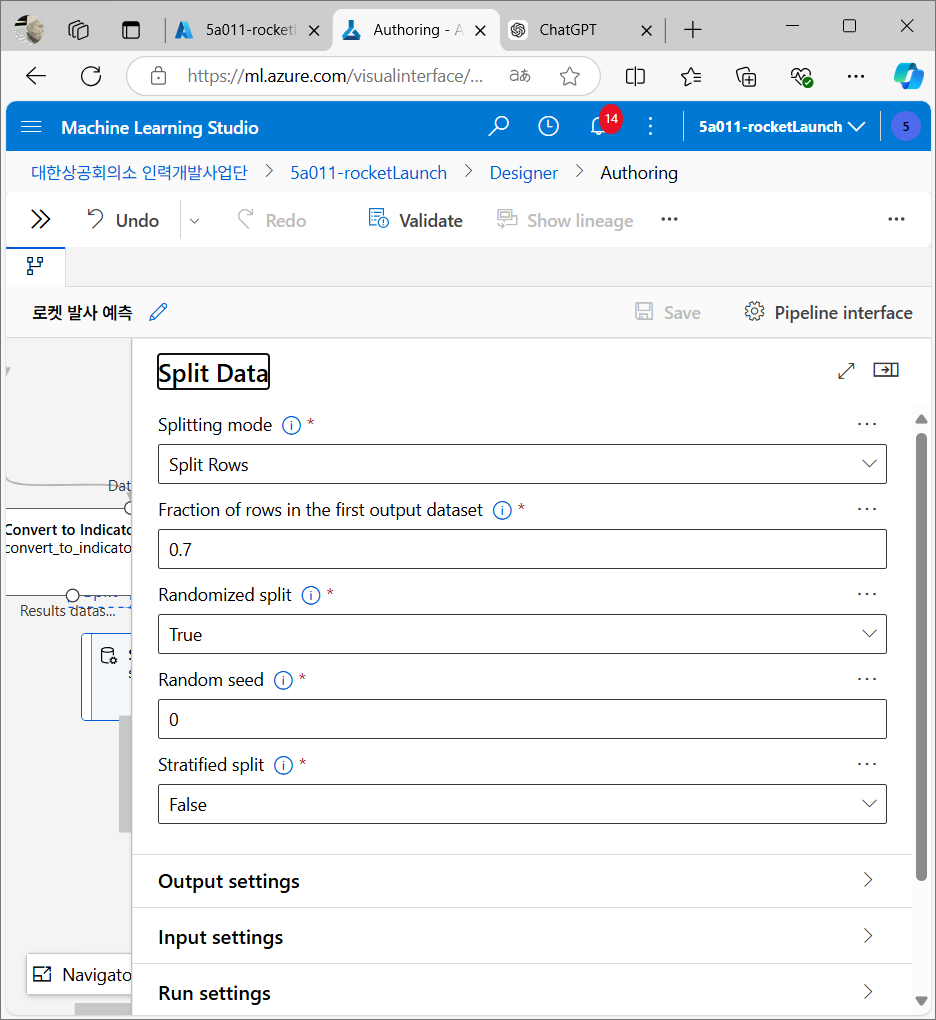
데이터 분리

수집한 데이터를 두 그룹으로 나누는데, 하나는 학습 데이터로 사용하고, 다른 하나는 테스트 데이터로 사용한다. 학습 데이터는 모델이 패턴을 배우는 데 사용되고, 테스트 데이터는 모델이 예측을 잘하는지 평가하는 데 사용된다.

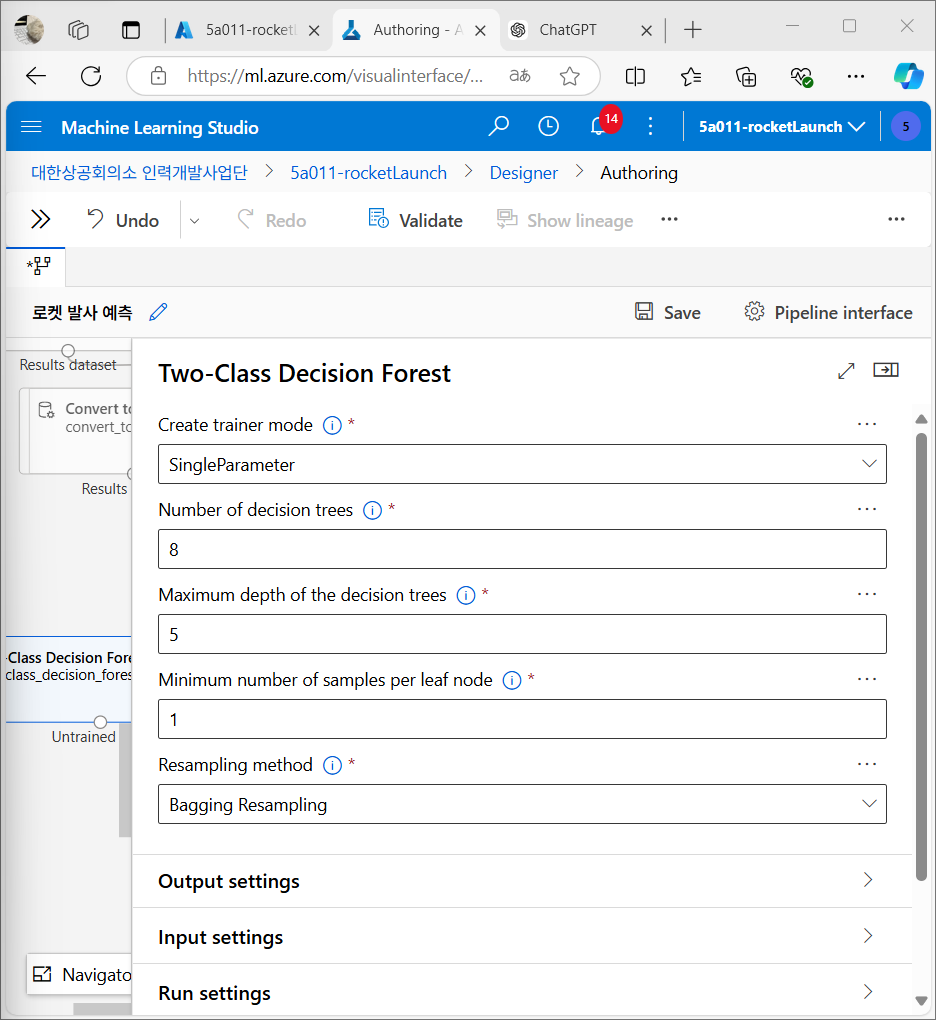
모델링 알고리즘 선택

로켓 발사를 예측하기 위해 랜덤 포레스트(Random Forest) 알고리즘을 사용할 것. 랜덤 포레스트는 의사결정 나무 여러 개를 만들어 각각의 예측 결과를 종합해 결론을 내리는 방식이다.

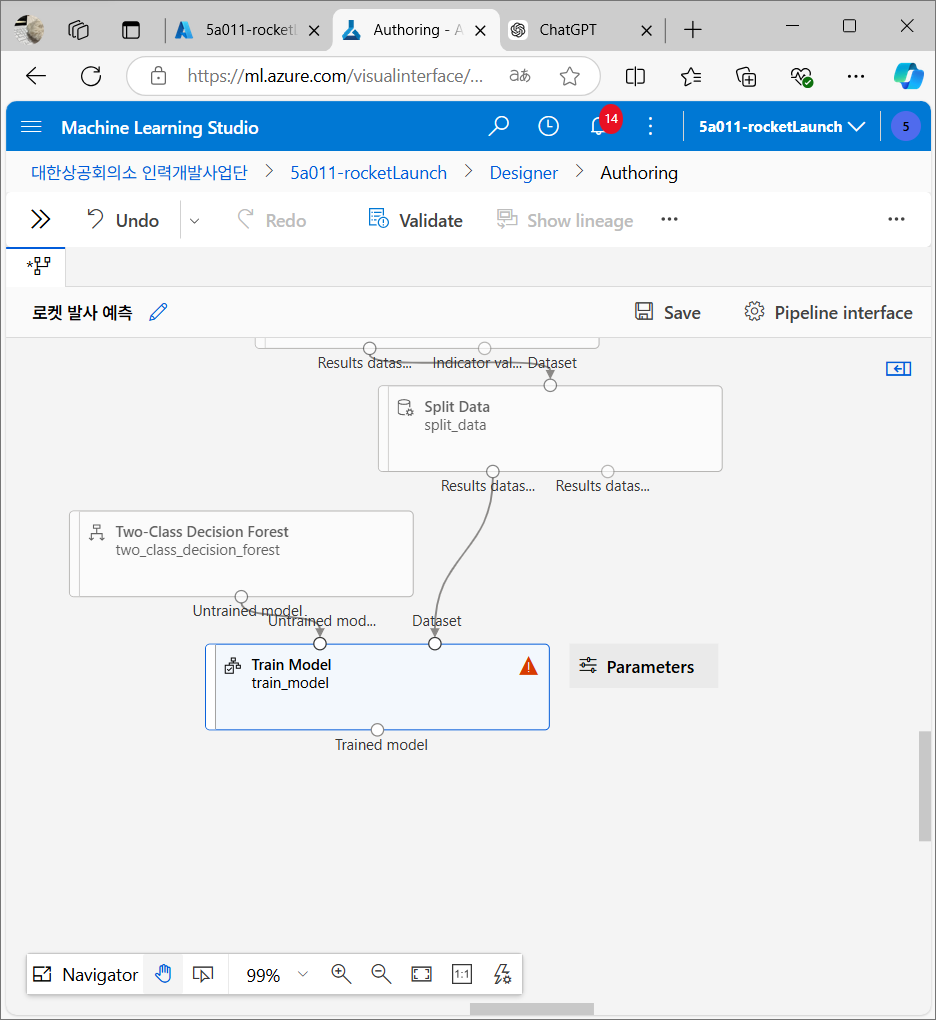
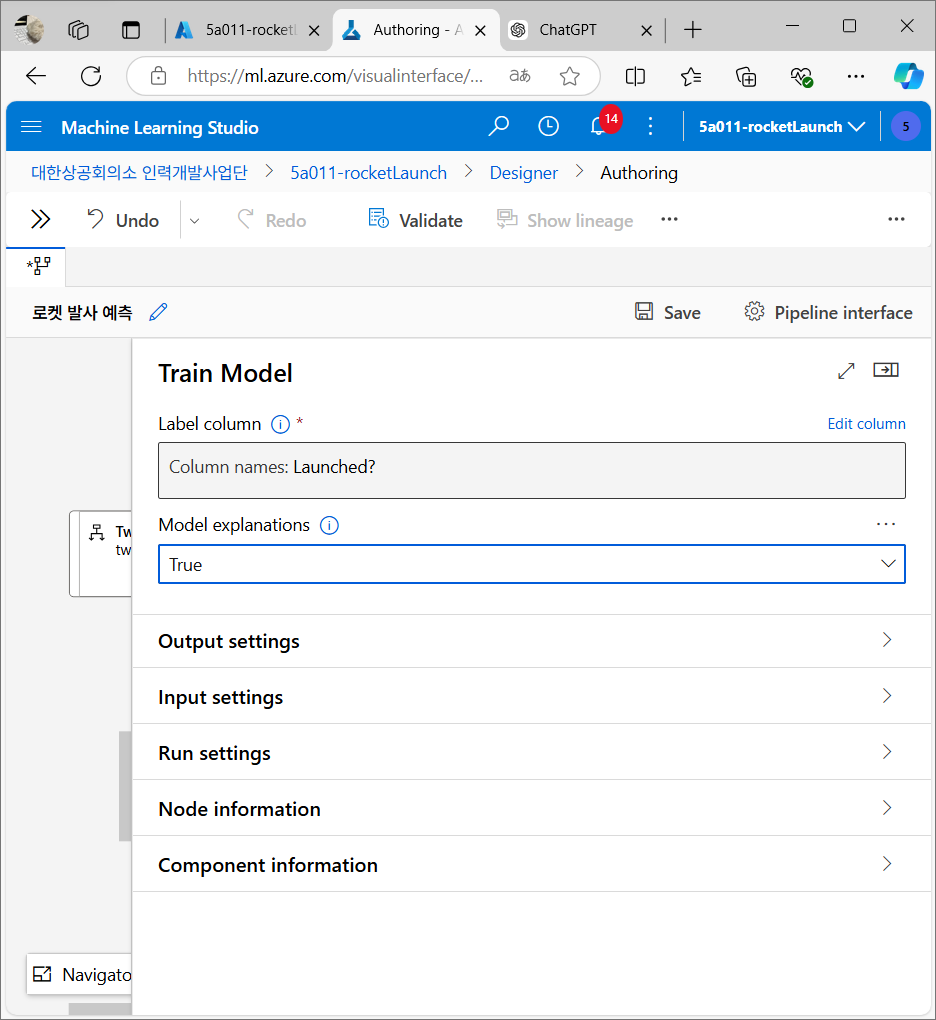
모델 훈련

훈련 데이터(전체 데이터의 70%)를 사용해 모델을 학습시킨다. 이 때 중요한 것은 로켓 발사 여부가 기록된 Launched? 항목을 모델이 예측하도록 학습시키는 것이다.

모델 테스트

학습이 끝난 모델을 실제로 테스트한다. 나머지 30%의 데이터로 모델이 얼마나 정확하게 예측하는지 확인하는 과정.

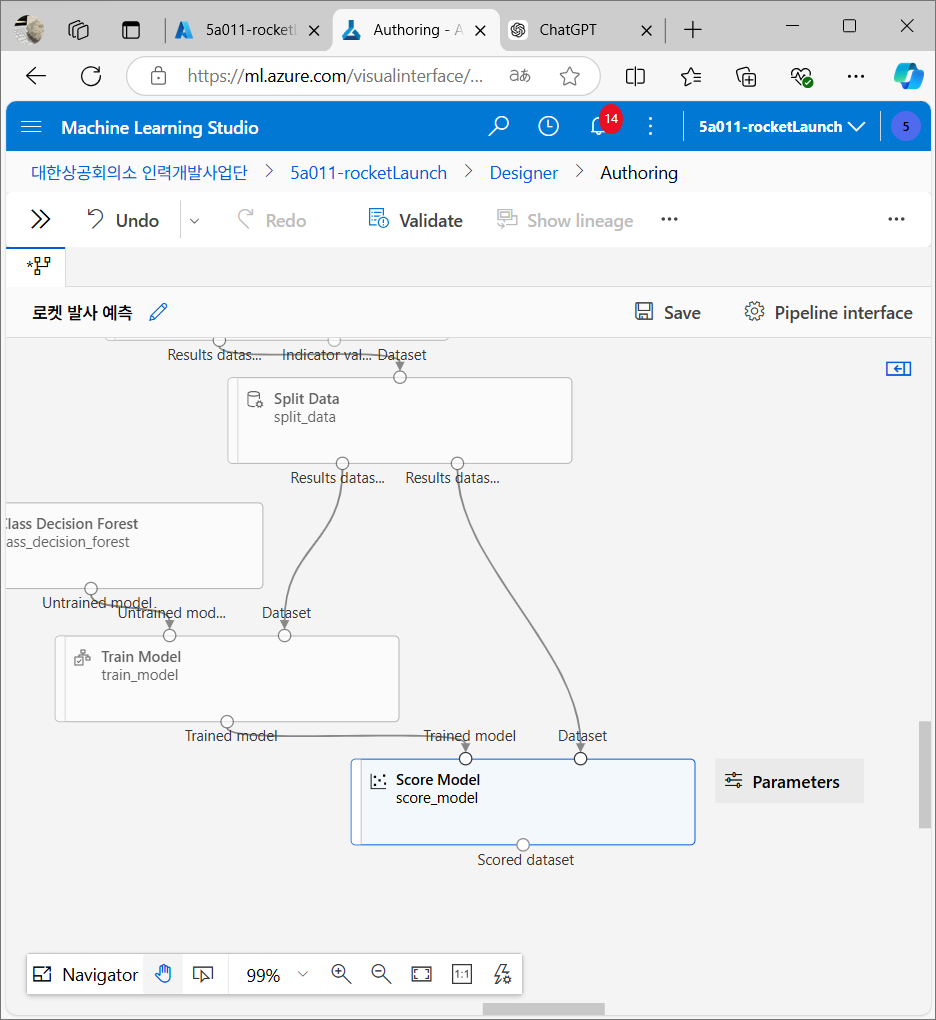
모델 평가

테스트가 끝나면 정확도(Accuracy), 정밀도(Precision), 재현율(Recall) 등의 지표를 통해 모델 성능을 평가한다. 이 지표들은 모델이 실제 로켓 발사 여부를 얼마나 정확하게 맞췄는지 평가한다.

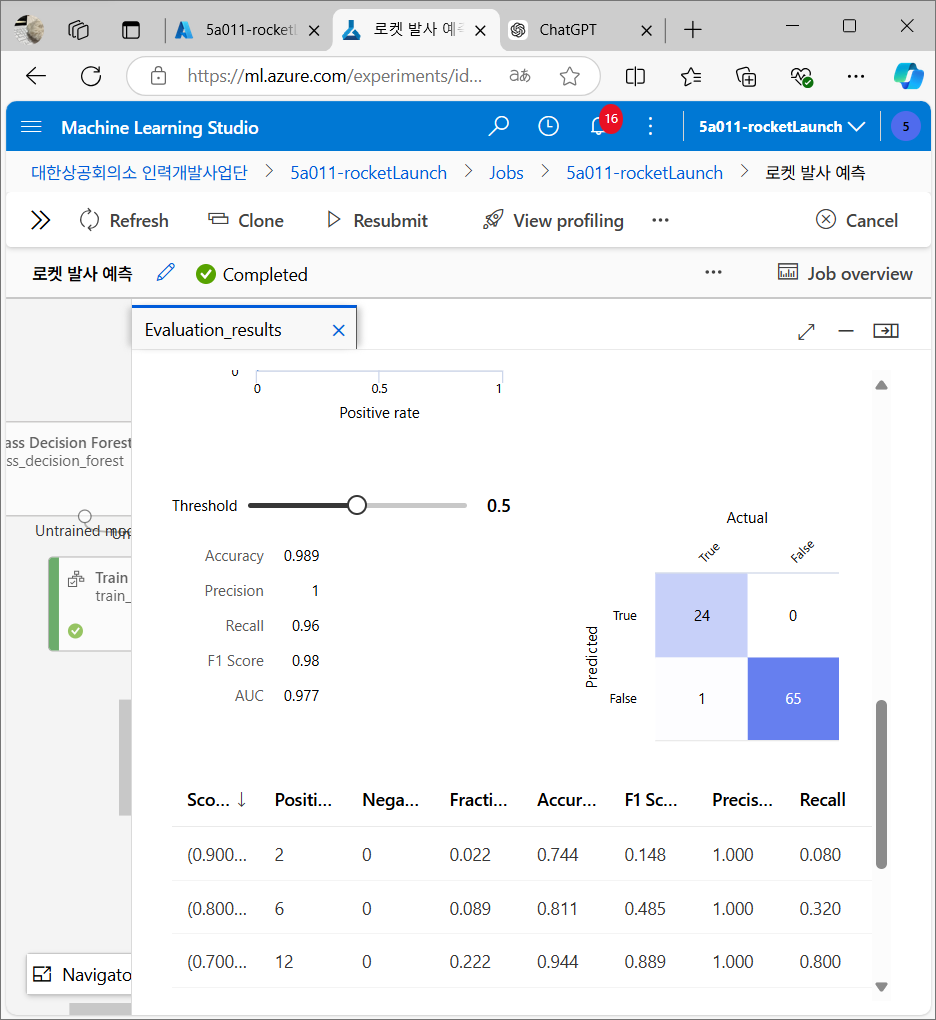
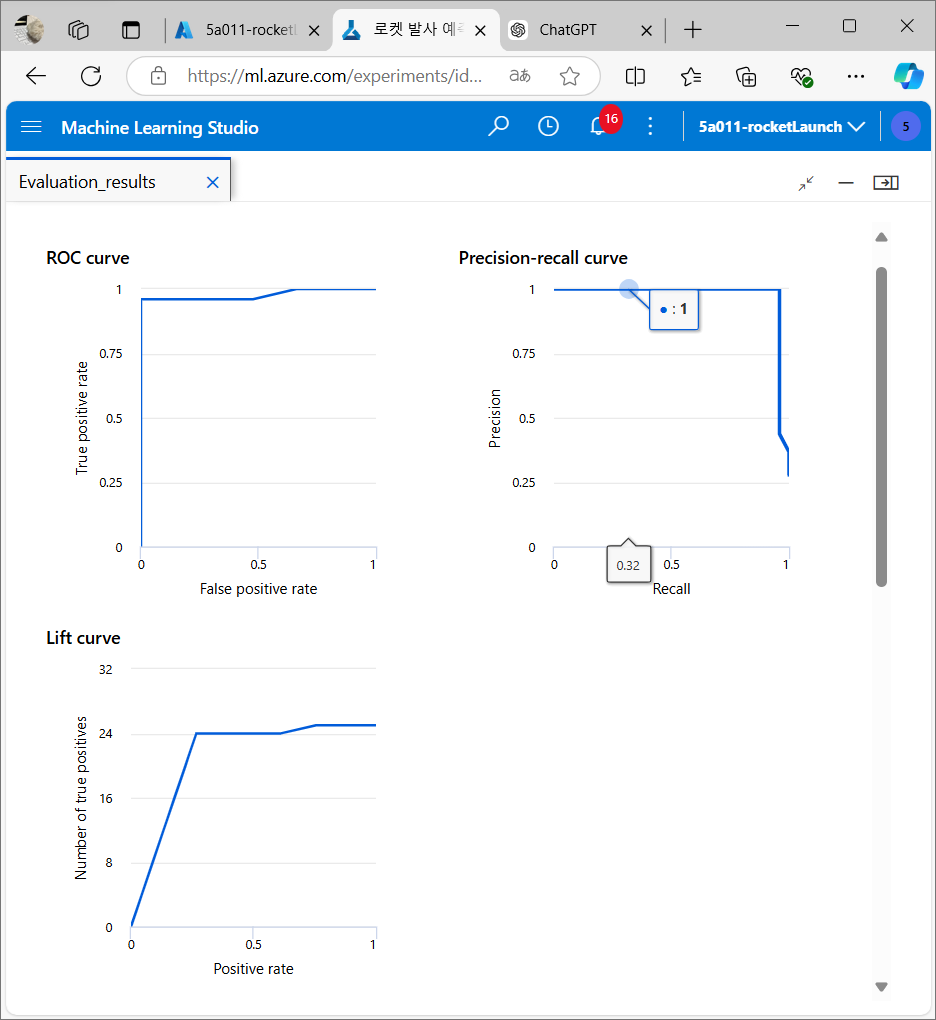
결과 분석

평가 후 모델이 얼마나 잘 예측했는지 평가 지표들을 분석한다.

자전거 렌탈 수요 예측 모델

회귀 모델

회귀(Regression)는 독립 변수(입력 데이터)와 종속 변수(결과 값) 사이의 관계를 찾고 이를 이용해 미래 값을 예측하는 모델이다.

• 독립 변수: 기온, 습도, 바람 세기, 계절
• 종속 변수: 자전거 대여 수요

선형 회귀(Linear Regression)

가장 기본적인 회귀 모델은 선형 회귀(Linear Regression) 이다. 선형 회귀는 입력 변수와 출력 변수 간의 관계가 직선으로 설명될 수 있을 때 사용하는 방법이다.

기온이 높아질수록 자전거를 더 많이 빌린다.

• $\hat{y}$: 예측값 (자전거 대여량)
• $x_1, x_2, x_3, \cdots, x_n$: 독립 변수들 (기온, 습도, 바람 등)
• $w_1, w_2, w_3, \cdots, w_n$: 각 독립 변수에 곱해지는 가중치
• $b$: 절편 (모든 독립 변수가 0일 때 예측되는 값)

단순 선형 회귀 vs. 다중 선형 회귀

• 단순 선형 회귀(Simple Linear Regression)
  단순 선형 회귀는 하나의 변수만을 고려해서 결과를 예측하는 방법이다.

  기온이 자전거 대여량에 미치는 영향을 하나만 보고 예측할 때 사용

  $\hat{y} = wx + b$
• 다중 선형 회귀(Multiple Linear Regression)
  다중 선형 회귀는 여러 독립 변수를 동시에 고려하는 모델이다. 날씨, 계절, 휴일 여부 등 다양한 데이터를 함께 사용해 예측할 때 이 방법을 사용한다.
  $\hat{y}=w_1x_1 + w_2x_2 + w_3x_3 + \cdots + w_nx_n + b$

오차와 손실(Loss)

회귀 모델을 만들 때, 예측한 값과 실제 값 사이의 오차(잔차, Residuals) 를 최소화하는 것이 중요하다. 오차가 적을수록 모델이 데이터를 잘 학습한 것.

• 오차(잔차): 실제 자전거 대여량 - 예측된 자전거 대여량
  이 오차를 최소화하기 위해서는 손실 함수(Loss Function) 를 사용한다. 회귀 모델에서는 주로 평균 제곱 오차(MSE)나 평균 절대 오차(MAE) 를 사용한다.
• MSE (Mean Squared Error)
  $MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$

  - $$y_i$$: 실제 값
  - $$\hat{y}_i$$: 예측 값
  - n: 데이터의 개수

• MAE (Mean Absolute Error)
  $MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$

경사 하강법(Gradient Descent)

경사 하강법(Gradient Descent)은 회귀 모델을 학습 시키는 방법 중 하나이다. 가중치 w와 절편 b 값을 조정해 오차를 줄이는 방향으로 이동하는 방법이다.
1. 모델은 먼저 임의의 가중치와 절편 값을 설정한다.
2. 그 다음 예측값과 실제값의 차이를 계산한다.
3. 이 차이를 줄이는 방향으로 가중치와 절편을 업데이트한다.

• $w^+$: 업데이트된 가중치
• $\eta$: 학습률(Learning rate, 한 번에 얼마나 많이 이동할지 결정하는 값)
• $\frac{\sigma E}{\sigma w}$: 기울기(Gradient)

거리

거리란 두 점 사이의 차이를 의미하는데, 머신러닝에서는 이 거리를 사용해 데이터 포인트 간의 유사도나 차이를 계산한다.

자전거 대여량 예측 시 모델이 예측한 값과 실제 값의 차이를 거리로 나타낼 수 있다. 거리가 작을수록 모델이 더 정확하게 예측한 것!

• L1 거리(맨해튼 거리): L1 거리는 두 점 사이의 거리를 직선으로만 계산한다. 수직과 수평으로만 이동하는 방식.

  $L1 \text{ norm} = |a| + |b|$

  예측한 자전거 대여량과 실제 대여량의 차이를 절대값으로 더하는 방식

• L2 거리(유클리드 거리): L2 거리는 직선 거리로 계산한다. 두 점 사이의 가장 짧은 거리, 즉 직선 경로를 이용하는 방식.

  $L2 \text{ norm} = \sqrt{a^2 + b^2}$

  예측한 자전거 대여량과 실제 대여량의 차이를 제곱해 더한 후, 그 값을 제곱근으로 구하는 방식

과대적합(Overfitting)

과대적합은 머신러닝 모델이 훈련 데이터에 너무 잘 맞춰져서 새로운 데이터(테스트 데이터)에서는 성능이 떨어지는 현상이다.

규제(Regularisation)

규제는 과대적합을 방지하기 위해 모델의 복잡성을 줄이는 방법으로 모델이 훈련 데이터에 지나치게 적합하지 않도록 하는 패널티를 추가하여 모델의 가중치를 제한하는 방식으로 작동한다.

• L1 규제(Lasso Regression)
  - 가중치의 절대값 합에 패널티를 추가
  - 일부 가중치를 0으로 만들어 변수를 선택할 수 있게 해준다. 즉, 중요하지 않은 특성은 모델에서 제거된다.
  $L1 \text{ norm} = |w_1| + \cdots + |w_n|$

  $E(W) = MSE + \lambda L_1 norm$

• L2 규제(Ridge Regression)
  - 가중치의 제곱 합에 패널티를 추가
  - 모든 가중치 값을 작게 만들어, 모델의 복잡성을 줄이지만 모든 특성을 남겨둔다.
  $L2 \text{ norm} = \sqrt{w_1^2 + \cdots + w_n^2}$

  $E(W) = MSE + \lambda L_2 norm$

머신러닝 모델 만들기

데이터 수집

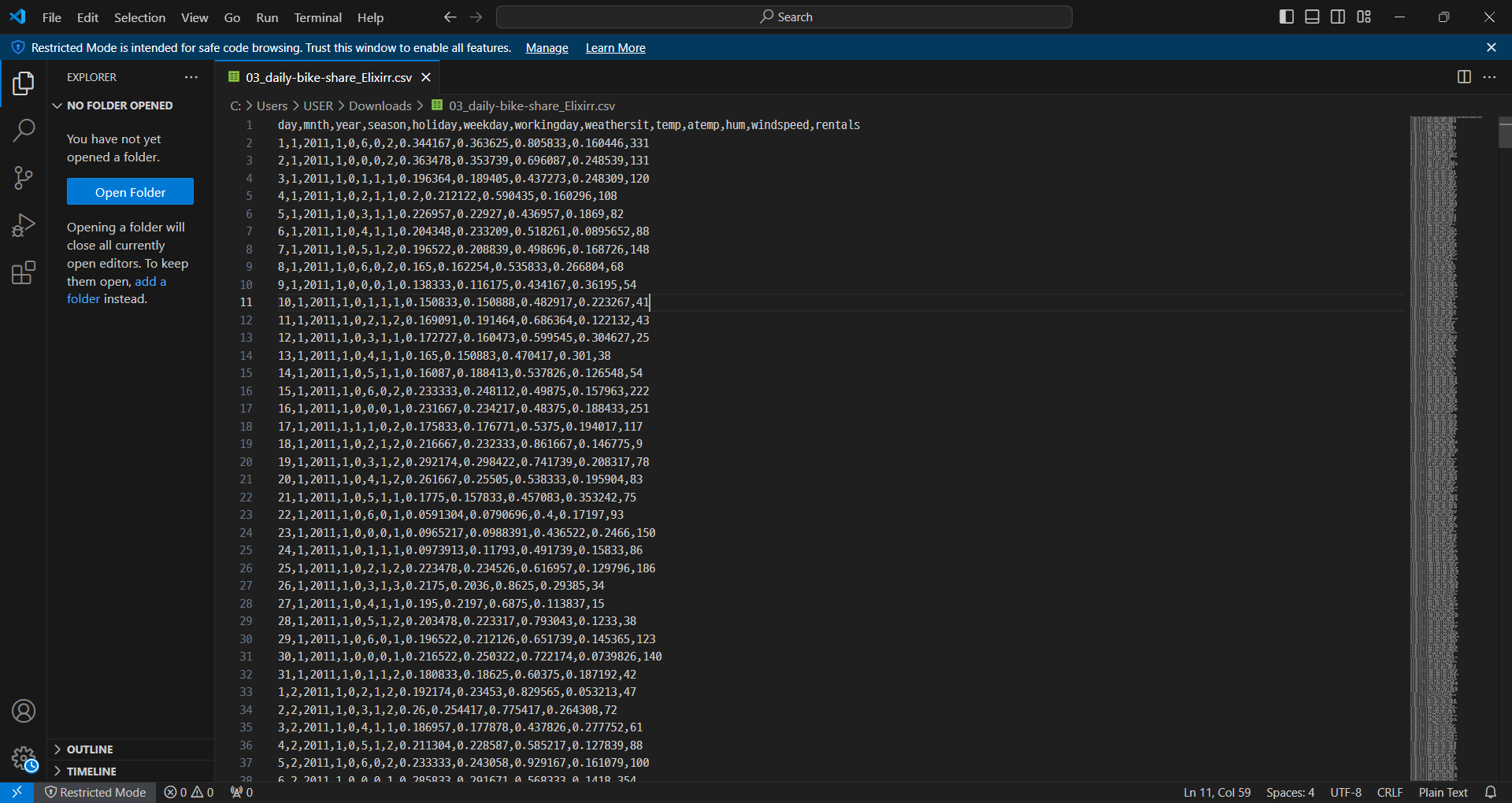
데이터 준비

• 결측치(Missing Data): 데이터가 없는 부분을 채우거나 제거한다.

  예: 특정 날의 기온 정보가 없는 경우 데이터 채워주기

• 데이터 정규화(Normalisation): 각 데이터의 단위가 다르면 모델이 잘못된 결론을 내릴 수 있다. 그래서 데이터를 0에서 1 사이의 값으로 변환해서 범위를 비슷하게 맞춘다.

  예: 기온은 0에서 30도까지 있지만 습도는 0에서 100까지 있다. 범위가 다른 값을 정규화해줘야 모델이 더 정확하게 예측할 수 있다.

데이터 정규화(Normalisation)

가장 일반적인 정규화 방법은 Min-Max Scaling이다.

• $x'$: 정규화된 값
• $x$: 원래 값
• $x_{min}$: 데이터셋에서의 최소값
• $x_{max}$: 데이터셋에서의 최대값
  이렇게 정규화를 수행하면 데이터가 항상 0과 1 사이의 값으로 변환된다.

데이터 표준화(Standardisation)

표준화는 데이터 평균이 0이고, 표준편차가 1인 정규 분포로 변환하는 과정이다. 이 방법은 Z-score normalisation이라고도 불린다.

• $x'$: 표준화된 값
• $x$: 원래 값
• $\mu$: 데이터셋의 평균
• $\sigma$: 데이터셋의 표준편차

기준	정규화(Normalisation)	표준화(Standardisation)
범위	0과 1 사이	평균 0, 표준편차 1
사용 목적	데이터의 크기를 일정하게 맞추기 위해	데이터 분포의 중심을 맞추기 위해
적용 알고리즘	거리 기반 알고리즘에 효과적	통계적 가정이 필요한 알고리즘에 효과적

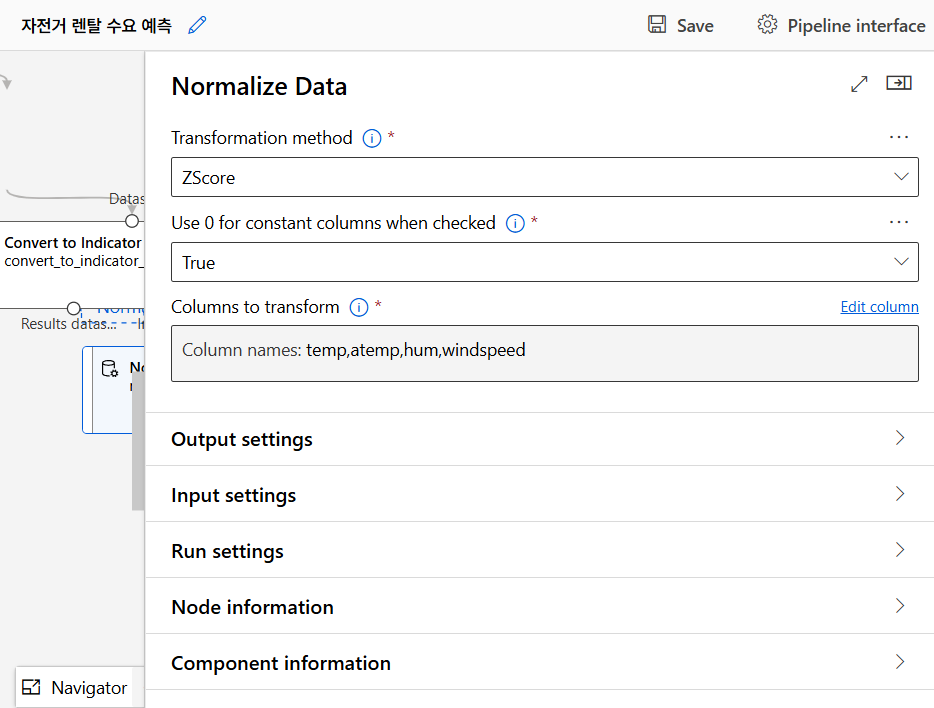
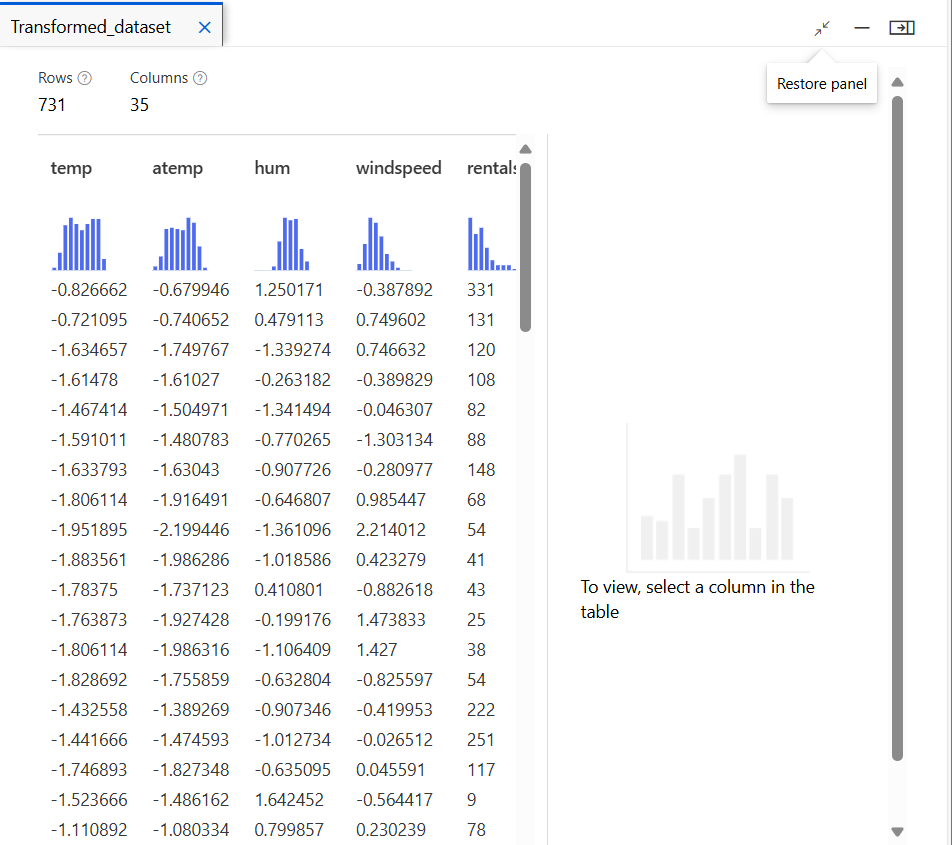
모델 만들기

자전거 대여량 예측을 위해 다중 선형 회귀(Multiple Linear Regression) 방법 사용

모델 학습

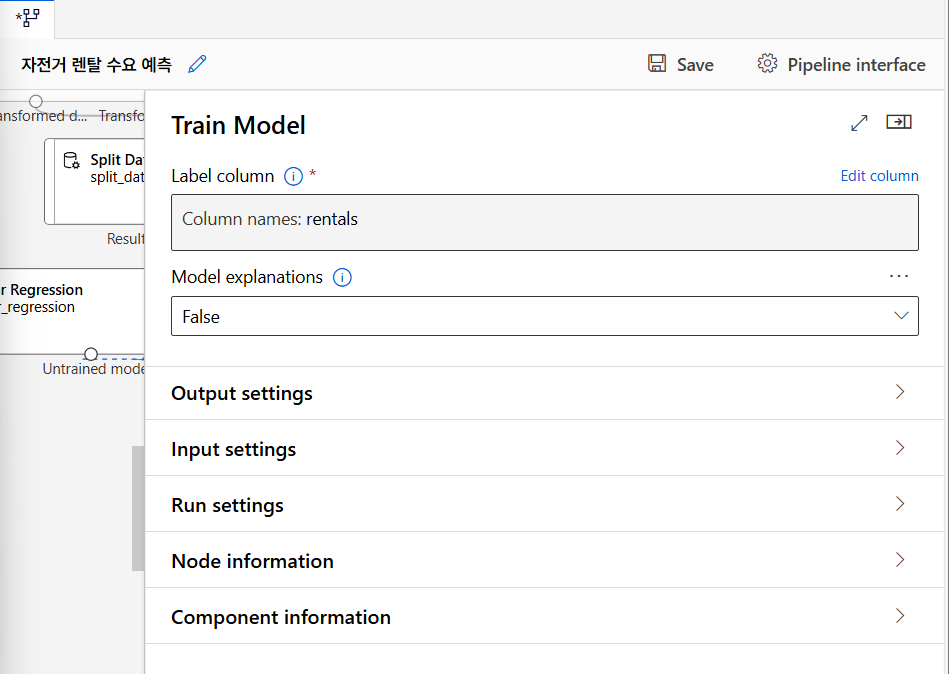
모델 평가

• 평균 절대 오차(MAE: Mean Absolute Error)
  실제 값과 예측 값 차이의 절대값을 평균한 값. 오차의 절대값을 사용하므로 모든 오차가 동일하게 반영됨.

  $MAE = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y_i}|$

  단순하고 해석하기 쉬운 지표이며 이상치(outlier)에 덜 민감하다.

• 평균 제곱 오차(MSE: Mean Squared Error)
  실제 값과 예측 값의 차이를 제곱한 후 평균한 값. 제곱을 사용함으로써 큰 오차에 더 큰 페널티를 부과.

  $MSE = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y_i})^2$

  모든 오차를 제곱하므로 큰 오차에 더 민감하게 반응하기 때문에 모델이 극단적인 오류를 최소화하도록 학습하는 데 유리하다.

• 루트 평균 제곱 오차(RMSE: Root Mean Squared Error)
  MSE의 제곱근으로, 예측 오차의 표준편차를 의미한다. MSE의 장점을 살리면서 단위가 실제 데이터와 동일하게 유지된다.

  $RMSE = \sqrt{MSE} = \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \hat{y_i})^2}$

  모델의 예측 성능을 쉽게 해석할 수 있도록 도와주며, 원래의 데이터 단위와 일치하기 때문에 직관적으로 이해하기 쉽다.

• 상대 절대 오차(RAE: Relative Absolute Error)
  모델의 예측값과 실제값 간의 절대 오차를 실제값의 평균과 비교하여 나타내는 지표이다. 예측 오차를 상대적 관점에서 평가하여 모델 성능을 다른 모델이나 기준과 비교할 수 있게 해준다.

  $RAE = \frac{MAE}{\frac{1}{n} \sum_{i=n}^n |y_i - \bar{y}|}$

• 상대 제곱 오차(RSE: Relative Squared Error)
  모델의 예측값과 실제값 간의 제곱 오차를 실제값의 평균 제곱 오차와 비교하여 나타내는 지표이다.

  $RSE = \frac{MSE}{\frac{1}{n} \sum_{i=1}^n (y_i - \bar{y})^2}$

• 결정계수 ($R^2$: Coefficient of Determinatin)
  모델이 종속 변수를 얼마나 잘 설명하는지를 나타내는 지표이다. 0에서 1 사이의 값을 가지고, 1에 가까울수록 모델의 설명력이 높음을 의미한다.

  $R^2 = \frac{SSR}{SST} = \frac{SST - SSE}{SST} = 1 - \frac{SSE}{SST}$

  $R^2 = 1 - \frac{\sum (실측 - 예측)^2}{\sum (실측 - 평균)^2}$

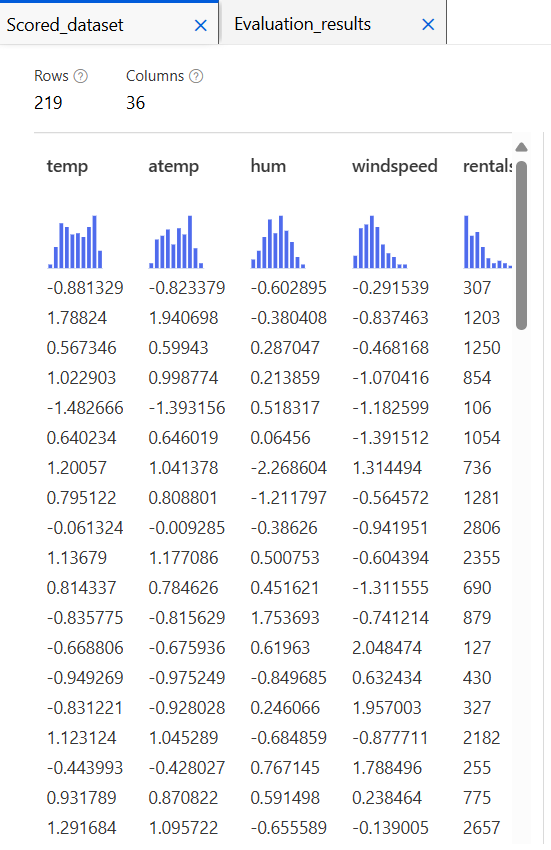
프로야구 선수 능력 측정 모델

PCA 주성분 분석

PCA(Principal Component Analysis)

고차원 데이터를 저차원으로 변환하면서도 원래 데이터가 가진 정보(분산)를 최대한 유지하려는 기법. 머신러닝에서 자주 사용되는 차원 축소 방법 중 하나이다.

• 차원의 저주(Curse of Dimensionality): 데이터의 차원이 커질수록(변수가 많아질수록) 계산이 어려워지고 과적합(overfitting)의 위험이 커진다. 이를 해결하기 위해 PCA로 차원을 줄이는 것.
• 데이터 시각화: 고차원 데이터를 2차원 또는 3차원으로 줄여 시각화가 가능하다.
• 모델 효율성: 모델의 속도와 성능을 향상시킨다.

주성분(Principal Components)

• 데이터의 분산(variance)을 최대화하는 새로운 좌표 축
• 주성분은 데이터의 가장 큰 변동성을 잡아내는 방향이다. 주성분1(PC1)은 가장 큰 분산을 설명하고, 주성분2(PC2)는 그 다음으로 큰 분산을 설명하는 식으로 차례로 나온다.

PCA의 과정

1. 데이터 표준화
   각 변수의 단위가 다를 경우 분석 결과가 왜곡될 수 있으므로 모든 변수의 평균을 0으로 만들고 분산을 1로 맞추는 표준화(standardisation) 가 필요하다.
2. 공분산 행렬 계산
   데이터의 각 변수들이 서로 어떻게 변화하는지(상관관계)를 계산한다. 이를 공분산 행렬로 나타낸다. 공분산이 크면 두 변수가 서로 강하게 연관되어 있는 것.
3. 고유 벡터와 고유값 계산
   • 공분산 행렬로부터 고유벡터(eigenvector)와 고유값(eigenvalue) 을 계산한다.
   • 고유벡터는 새로운 축(주성분)이고, 고유값은 해당 주성분의 중요도를 나타낸다. 고유값이 클수록 그 축이 더 많은 데이터를 설명할 수 있다.
4. 주성분 결정
   • 각 변수에 대한 공분산을 분석한 후, 주성분을 계산
   • 일반적으로 고유값이 큰 순서대로 주성분을 선택한다. 주성분의 개수는 Scree Plot을 이용하여 결정한다. 이 그래프에서 엘보우 포인트(Elbow Point) 까지의 주성분을 사용한다.
5. 데이터 변환
   원래 데이터를 가장 많이 설명하는 주성분들을 새로운 좌표축을오 변환하고 불필요한 차원은 줄인다.

PCA 결과 해석

• 분산 비율(Explained Variance Ratio): 각 주성분이 데이터의 전체 분산 중 어느 정도를 설명하는지 비율로 나타낸 값.
• 누적 분산 비율(Cumulative Explained Variance): 주성분들을 차례대로 더할 때 그 주성분들이 전체 데이터를 얼마나 잘 설명하는지 나타낸 값

군집 알고리즘

군집화(Clustering)

군집화는 데이터의 유사성을 측정하여 비슷한 데이터끼리 모으는 작업이다 이를 위해 데이터 간 거리(distance) 를 측정하여 가까운 데이터들을 하나의 그룹으로 묶는다. 군집화에서 자주 사용하는 거리 측정방법으로는 유클리드 거리(Euclidean Distance), 맨해튼 거리(Manhattan Distance) 등이 있다.

• 유사도
• 응집도(Cohesion): 한 군집 내 데이터들이 얼마나 가까운가. 응집도가 높을 수록 군집 내 데이터들이 서로 유사
• 분리도(Separation): 군집 간의 차이가 얼마나 큰가. 분리도가 높을수록 서로 다른 군집 간의 차이가 크다.

군집화 알고리즘

• 분할적 군집화(Partitional Clustering)
  - K-means 군집화: K개의 군집을 설정한 후, 데이터를 해당 군집의 중심점(centroid)으로부터의 거리에 따라 분류하는 알고리즘. K는 사용자가 미리 정해줘야 한다.
  • DBSCAN(Density-Based Spatial Clustering of Applications with Noise): 밀도를 기반으로 군집을 나누는 방법. 데이터 포인트가 충분히 밀집된 영역을 군집으로 정의하고 밀도가 낮은 영역은 노이즈로 간주
• 계층적 군집화(Hierarchical Clustering)
  - 병합적 군집화(Agglomerative Clustering): 각각의 데이터 포인트를 하나의 군집으로 시작해 가장 가까운 군집을 반복적으로 병합하여 계층을 형성
  • 분할적 군집화(Divisive Clustering): 모든 데이터를 하나의 큰 군집으로 시작해 점차 군집을 분할하면서 계층을 형성하는 방법

유사도와 거리 측정

• 유클리드 거리(Euclidean Distance): 두 점 사이의 직선 거리를 계산하는 것. 2차원 공간에서 두 점 사이의 거리.
  $\sqrt{x_1^2 + x_2^2}$
• 맨해튼 거리(Manhattan Distance): 두 점 사이의 직교 축을 따라 이동한 거리를 계산하는 것.
  $|x_1| + |x_2|$
• 코사인 유사도(Cosine Similarity): 두 벡터 사이의 각도를 사용해 유사도를 측정하는 방법. 두 벡터가 이루는 각도가 작을수록 유사도가 높다고 판단.

군집화 평가

• SSE(오차 제곱합, Sum of Squared Error): 각 군집 내 데이터 포인트들이 군집 중심점과 얼마나 가까운지 평가. 이 값이 작을수록 군집화가 잘 된것으로 간주.
• 실루엣 계수(Silhouette Coefficient): 군집 내 데이터들의 응집도와 군집 간 분리도를 함께 평가하는 지표. 이 값은 -1에서 1 사이의 값을 가지며 1에 가까울수록 군집화가 잘된 것

데이터 병합

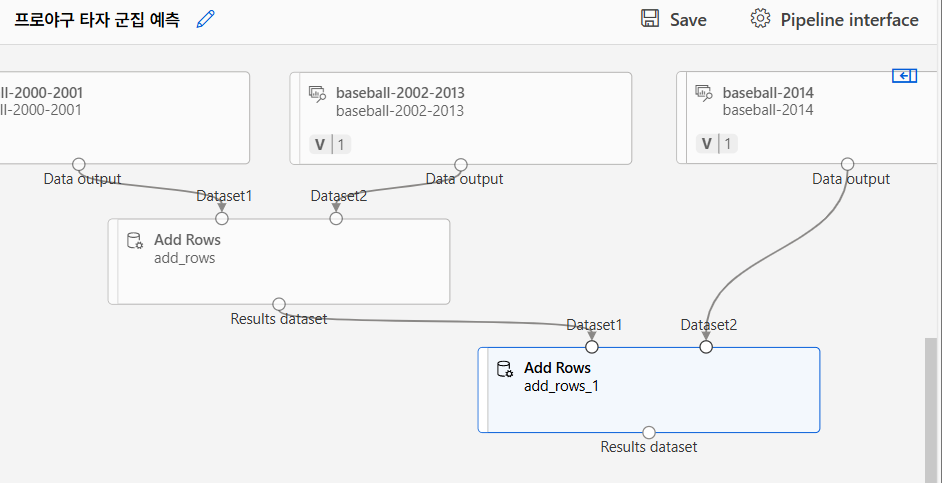
데이터 정규화 및 변환

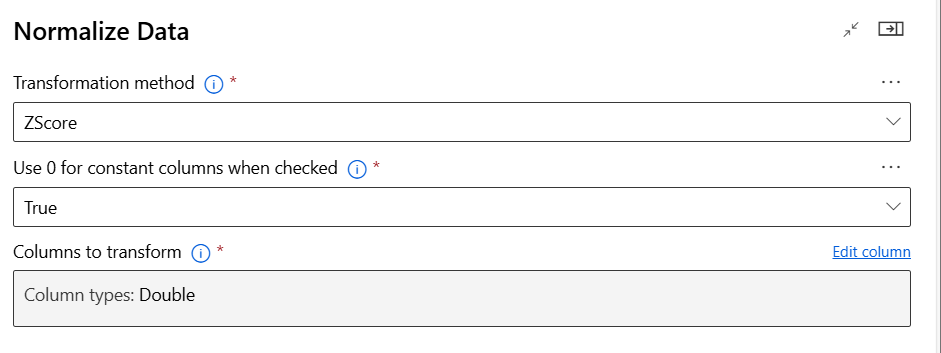
주성분 분석(PCA)

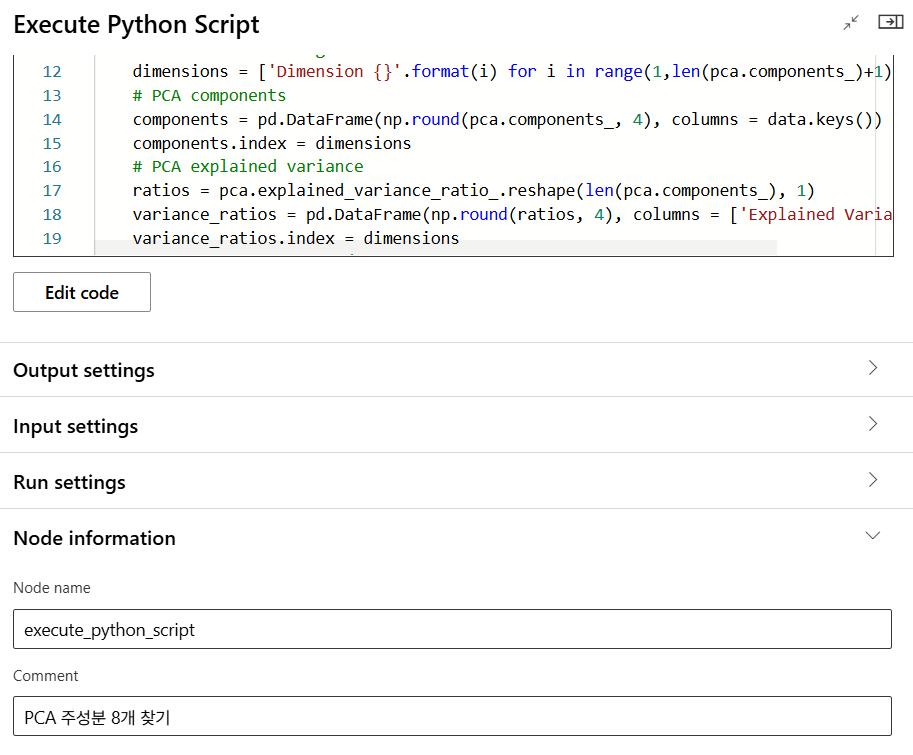
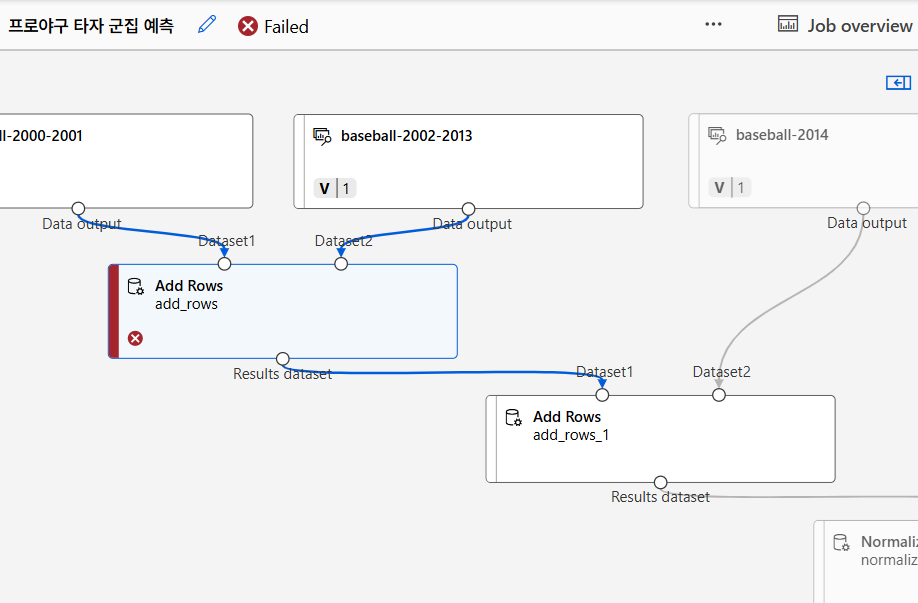
왠지 실행에 오류가 났으므로 나머지는 목요일에..

Personal Insight

실습이 연속으로 이어지다 보니 꽤 고되게 느껴지기도 하지만, 한 실습이 마칠 때마다 조금씩 성장하고 있는 걸까 싶은 마음에 괜히 뿌듯함이 든다. 매 순간이 도전이지만, 배우는 기쁨이 크고, 첫날엔 이해 못했을 많은 것들을 알아듣고 있는 모습도 보인다. 한 조각 씩 맞추다보면 언젠가 퍼즐이 완성되는 날이 있을까? 힘든 만큼 보람도 크고, 동기들도 강사님들도 다 너무 좋다. 단단해지는 중.