
하루 한 줄 요약
허리가 아파요....
오늘 공부한 내용
- 정렬(병합, 퀵, 힙, 도수/계수)
새로 배우게 된 내용
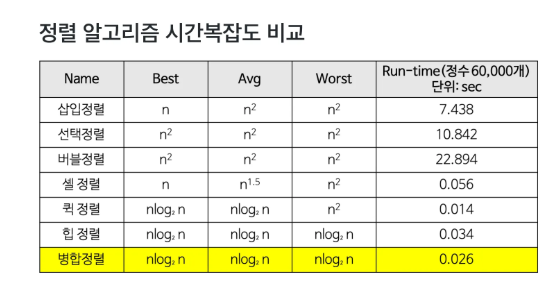
정렬(병합, 퀵, 힙, 도수/계수)
-
병합 정렬
앞 부분과 뒷 부분의 두 그룹으로 분리하고 각각 정렬하고 병합하는 방식으로 정렬
서로 떨어진 원소를 교환하지 않기에 Stable(안정적, 동일 원소 순서 보장) 하다.
시간 복잡도는 O(N log N) -
퀵 정렬
이름 답게 가장 빠르다는 알고리즘으로 중심축이라고 불리는 Pivot을 기준으로 정렬한다.
평균적으로 O(N log N) 의 시간 복잡도를 갖는다
단, 이미 정렬이 거의 완료된 상태같은 경우나 피벗이 한쪽 끝에 위치한 경우에는 최악의 경우 O(N^2)의 시간 복잡도를 갖는다. -
힙 정렬
루트에 최대값/최소값이 있는 힙 자료구조의 특성을 이용한 정렬이다.
파이썬에선 heapq 모듈을 사용해서 힙 자료구조를 구현할 수 있다.
다만 최소 힙으로 구현되기에 인덱스 0번(루트 노드)에는 최소값이 온 다는 것을 명심!
시간 복잡도는 O(N log N) 이다. -
최소힙에서 최대힙 전환 In python
(우선순위, 값) 형태의 튜플을 넘겨주고 우선순위에 음수를 곱해서 큰값부터 꺼낼 수 있는 최대힙으로 만들어 주는 것.
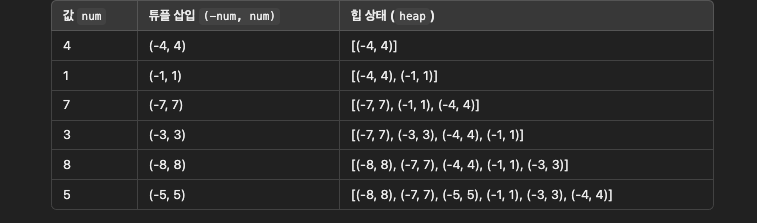
from heapq import heappush, heappop
nums = [4, 1, 7, 3, 8, 5]
heap = []
for num in nums:
heappush(heap, (-num, num)) # (우선 순위, 값)
while heap:
print(heappop(heap)[1]) # index 1 => 값, 여기서 0 넘겨주면 우선순위가 출력- 도수/계수 정렬(Counting Sort)
원소의 대소 관계 파악이 필요없고 키값도 비교할 필요가 없으며
무려 O(N)의 놀라운 속도를 갖고 있는 정렬 법
아이디어는 단순하게, 해당 배열에서 각 숫자가 몇개 나오는지 저장해놓고, 이걸 갯수대로 나열하는 것
근데 이걸 코드로 구현하는 부분이 잘 이해가 가지 않았다.
백준 2570/2571/10989 번 다양한 정렬로 풀어보기
모두 수를 정렬하는 문제이지만 차이가 있다.
바로 N이 1000 / 1,000,000 / 10,000,000 으로 차이가 있다.
따라서 각각 O(N^2) 이하, O(N log N) 이하, O(N) + 메모리 관리
이렇게 세가지 방법으로 풀어야 한다.
- 2570
그래서 2570에서 O(N^2)의 시간 복잡도를 가진 선택정렬로 푸니 60ms가
퀵정렬과 힙정렬로 풀때는 40ms 대를 유지하는 것을 확인.
또한 TimSort라는 방식을 활용하는 sorted() 메서드 만이 36ms로 유일하게 30ms 이하를 기록했다.
- 2571
N이 1,000,000 이하가 되니 선택정렬을 활용한 풀이는 시간 초과가 발생했다.
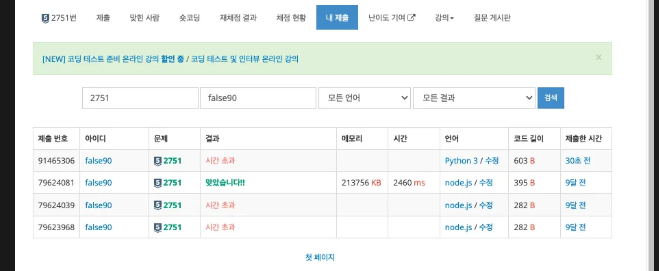
또한 이때 퀵정렬과 sorted() 활용한 풀이의 시간차이가 별로 없을줄 알았는데 생각보다 4044ms 와 1288ms로 차이가 많이 나서 공부를 좀 해보니
퀵정렬은 최악의 경우 O(N^2)가 나올 수 있다는 것을 망각...(방금 공부했잖어...)
여튼 다양한 정렬로 문제를 풀어보며 개념을 익힐 수 있었다.
- 10989
이 문제 같은 경우 N이 1억이며 메모리 제한 역시 8MB로 빡빡한 제한을 둔다.
따라서 O(N)의 시간 복잡도를 가진 계수/도수 정렬을 활용해야하며, 딕셔너리 자료형 등을 통해
저장한 값을 다시 쓰면서 메모리를 아껴야 했다.
계수/도수 정렬 코드를 꾸역꾸역 구현해도 메모리측면을 생각하지 못해서 많은 시간이 소요되었던 문제
여전히 메모리 측면에서 기존 코드와 딕셔너리를 통해 꺼내쓰는 코드의 차이를 명확히 설명할 수 없어서
내일 다시 한번 공부할 예정.
공부하면서 어려웠던 점
재채기 했는데 허리가 아파요...
그래서 오래 못앉아 있어서 오늘은 공부한 양이 많이 않습니다 ㅠㅠㅠ
건강도 실력이다!ㅠ
