[EEND-GLA 리뷰] Towards Neural Diarization for Unlimited Numbers of Speakers using Global and Local Attractors

소개

• 이 글은 논문을 읽고 정리하기 위한 글입니다.
• 내용에 오류가 있는 부분이 있다면 조언 및 지적 언제든 환영입니다!

ASRU 2021 에 올라온 논문입니다. (Paper)

Citation

@misc{horiguchi2021neural,
      title={Towards Neural Diarization for Unlimited Numbers of Speakers Using Global and Local Attractors}, 
      author={Shota Horiguchi and Shinji Watanabe and Paola Garcia and Yawen Xue and Yuki Takashima and Yohei Kawaguchi},
      year={2021},
      eprint={2107.01545},
      archivePrefix={arXiv},
      primaryClass={eess.AS}
}

Introduction

Background

• EEND-EDA 이전 포스팅 내용 참고

Previous Limitation

• EDA의 한계점
  • 학습되지 않은 화자 수에 대해서는 예측하지 못하는 현상을 보임
  • 원인 분석 과정에서 우선 5-6명에 대한 SA-EEND의 Embedding를 PCA Visualization 한 결과는 아래와 같다.
    
  • Transformer 의 Encoder가 각 Speaker 들을 의미있게 분산시키는 모습을 볼 수 있다.
  • 결국, EDA가 학습이 잘 되지 않았다고 생각하고, 본 논문은 이에 대한 개선 방안을 제안한다.

Main Proposal

• Global Attractors(Transformer Decoder)
  • Transformer Decoder 를 이용하여 LSTM에서 생성된 Local Attractor를 Query로 사용해 좀더 Global 한 정보를 담은 Local-Global Attractor 생성
• Pairwise(Affinity) Loss (Contrastive Loss?)
  • 본 논문은 EEND-Vector-Clustering와 유사하게 짧은 Chunk 내에서 Speaker(Local-global) Attractor들을 생성하고 이 관계를 Pairwise Loss 를 이용하여 유사성을 modeling한다.
  • EEND-vector-Clustering과 달리 화자 인식 정보를 사용하지 않고 Attractor 간의 유사성을 EDA와 Transformer Decoder에서 모델링 할 수 있도록 했다.
• Proposed new Clustering Method for Inference
  • 본 논문에서는 기존 Auto-Tune Spectral Clustering를 Pairwise Loss의 Distance Matrix 형식을 고려한 개량된 Clustering 방식을 제안한다.
  • 솔직히 Spectral Clustering 과 Auto-Tune Spectral Clustering 에 대한 이해가 부족하여 제대로 된 설명을 하기 힘들 것 같다...

Proposed Method

Intro

• 전반적인 모델 구조는 크게 6가지로 볼 수 있다.
• 1) Stacked Transformer Encoders (SA-EEND)
• 2) Split into sub-sequences
• 3) Local EDA
• 4) Transformer Decoder for Global Attractor
• 5) Exist Loss and Diarization Loss
• 6) Pairwise(Affinity) Loss

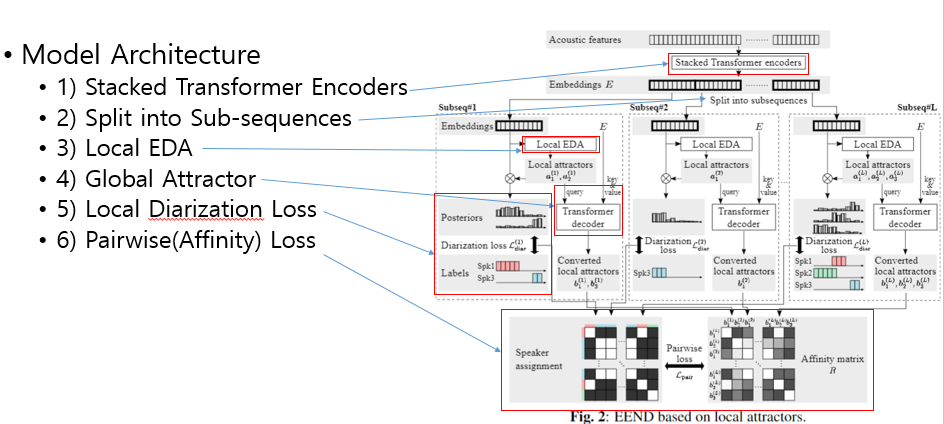
Architecture

• 1) Stacked Transformer Encoder (SA-EEND)
  • 기존 SA-EEND와 동일
  • $E=Encoder(X) \in(T\times D)\rarr(500 \times 256)$

• 2) Split into Sub-sequences
  • 생성된 Embedding $E$를 일정 시간 간격으로 자름
  • 본 논문은 5초로 자름
  • $E=(500 \times 256)\rarr E^{(l)}=(10 \times 50 \times 256)$

• 3) Local EDA
  • 기존 EEND-EDA 와 동일한 구조와 Loss를 사용한다.
  • LSTM 기반 Encoder-Decoder를 이용하여 Local한 5초 내에서의 Speaker Attractor를 예측한다.
    $A_{l}=a_{1}^{(l)},a_{2}^{(l)},...=EDA(E^{(l)})$

• 4) Transformer Decoder for Global Attractor
  • 현재 l번째 5초 chunk정보 뿐 아니라 전체 Embedding 정보를 이용하여 향상된 local attractor를 생성하는 방법
  • Transformer Decoder을 이용하여 EDA에서 생성된 local attractor를 Query 1)에서 생성된 전체 Embedding E 를 Key, Value 로 입력으로 하여, local-global 정보를 모두 담은 $b^{(l)}$ global attractor 생성
    $b^{(l)}=b_1^{(l)},...,b_{S_l}^{(l)}=TransformerDecoder(A_l,E)$

• 5) Exist Loss and Diarization Loss
  • 기존 EDA와 동일하게 Diarization Loss와 Exist Loss 사용
  • Exist Loss
    $\hat{z}_s^{(l)}=\sigma(\omega^Ta_s^{(l)}+b)\in(0,1),(s=1,2,...)\quad\quad z_s= \begin{cases} 1\;(s\in\{1,...,S\})\\ 0\;(s=S+1) \end{cases}\\ L_{exist}=\frac{1}{S+1}\sum_{s=1}^{S+1}BCE(z_s,\hat{z}_s)$
  • Diarization Loss
    $\hat{y}_{t,s}=\sigma((E_{t}^{(l)})^{T}a_s^{(l)})\in(0,1)\\ L_{diarization}=\frac{1}{TS}\argmin_{(\phi_1,...,\phi_T)\in\phi(1,...,T)}{\sum_{t=1}^{T}{\sum_{s=1}^{S}{BCE(y_{\phi_{t,s},\hat{y}_{t,s}})}}}$

• 6) Pairwise(Affinity) Loss
  • Variable
    - $S$: oracle speaker number
    - $S^{*}$: estimated speaker number
    - $b_i$: i번째 global speaker attractor
    - $c_i$: 전체 S^{*} 중 $i번째 global speaker attractor와 같은 attractor 개수 - $\delta: soft margin hyper-parameter 0.5
    - $r_{ij}$: i,j 번째 global speaker attractor가 같은 화자인지 여부
    - $[\ .\ ]_+$: Hinge Function

    $r_{ij}= \begin{cases} 1,\;\ if \ (i,\ j \ \ is\ same\ speaker) \\ 0,\;\ otherwise \end{cases}$

    $L_{pair}=\sum_{i,j\in{1,...,S^{*}}}{\frac{1}{S^2c_ic_j}\color{Red}(r_{ij}(1-sim(b_i,b_j))\color{Black}+\color{Cyan}(1-r_{ij})[sim(b_i,b_j)-\delta]_+),}\\ sim(b_i,b_j):=\frac{b_i^{T}b_j}{\|b_i\|\|b_j\|}$
• if i, j 가 same speaker : Red term
  • 같은 화자는 최대한 같은 embedding 값을 가져야 한다. 즉 $sim(b_i,b_j)\rarr1$에 가까워야함
• if i, j 가 diff speaker : Blue term
  • 다른 화자인 경우, $sim(b_i,b_j)<\delta$ 를 만족하도록, 즉 두 speaker embedding space 가 적어도 $\delta$ 만큼은 떨어져 있어야 함을 의미한다.

• 7) Total Loss
  $L_{both}=L_{local}+L_{global}$
  • Local Loss
    - Split 된 Local block 들에 대한 diarization loss와 EDA의 exist loss 의 평균과 pairwise loss를 더한 값을 사용함
    - $\alpha$: 1.0, $\gamma$: 1.0
    $L_{local}=\frac{1}{L}{\sum_{l=1}^{L}{(L_{diar}^{(l)}+\alpha L_{exist}^{(l)}})}+\gamma L_{pair}$
  • Global Loss
    - 본 논문에서는 Local loss 만을 사용하는 것은 느리고 불안정한 수렴 양상을 보였다고 한다.
    - 이러한 점을 보안하기 위해서, 기존 EEND-EDA 와 동일하게 전체 Embedding 을 동일한 EDA에 입력에 대한 결과를 이용하여 global loss를 사용했다.
    - $\alpha$: 1.0
    $L_{global}=L_{diar}+\alpha L_{exist}$

New Clustering Method for Inference

• 기존 Graph based Unsupervised Clustering Method는 사용 이전에 Hyper-parameter tuning 작업이 필요하다. (AHC(Agglomerative Hierarchical Clustering), SC(Spectral Clustering))

• 일반적으로 SC는 p nearest neighbor binarization를 통한 unreliable한 value를 제거함으로서 noise를 효과적으로 제거한다.

• "Auto-tuning spectral clustering for speaker diarization using normalized maximum eigengap" (Singal Processing Letters 2020) 논문에서는 NMS를 방법으로 Hyper-parameter p값을 Automatic 하게 정하는 알고리즘을 제안한다.

• 일반적인 Spectral Clustering 과정은 다음과 같다.
  • 1) Construct an Affinity Matrix
  • 2) Calculate its graph Laplacian
  • 3) Conduct eigen-value decomposition
  • 4) estimate the number of speakers based on the maximum eigengap
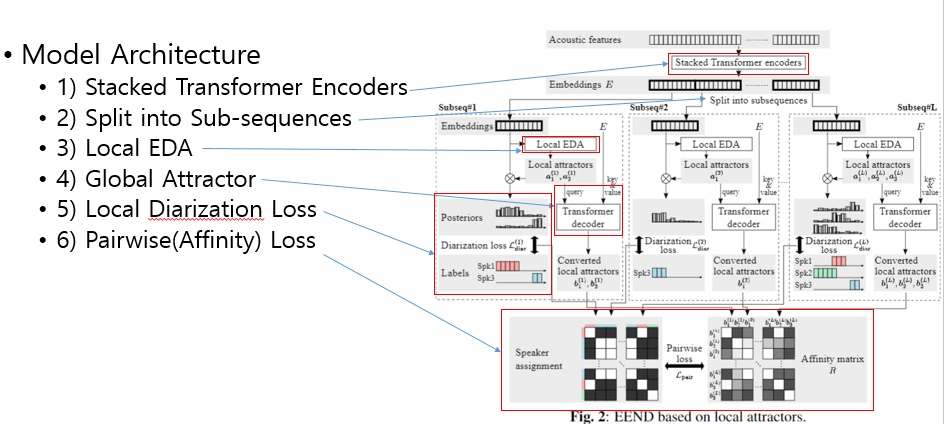
    - 아래 수식에서 $R$ (Affinity Matrix) 는 positive-semidefinte를 만족한다.
    - 위 결과 eigen-value $\lambda_i$들은 positive를 만족한다.
    - 여기서 $\hat{S}$값을 이용하여 maximum eigengap를 계산하여 의미있는 eigen-value 개수, 즉 최대 화자 수를 계산해 낸다.
    

• 본 논문에서의 변경된 Spectral Clustering은 다음과 같다.
  • 위에 일반적인 SC의 과정을 그대로 따르지만, 아래와 같은 변경점을 가진다.
  • EEND-vector-clustering의 Constrained Clustering 방법과 동일하게 $i,j$가 같은 chunk에서 나온 speaker attractor인 경우, 네트워크에서 서로 다른 speaker로 정한 것으로 이를 반영하여 cannot-link를 적용한다.
  • $i, j$가 다른 경우 기존 pairwise loss function의 형태와 비슷하게 hinge function으로 distance matrix를 구성한다. 서로 다른 경우 0의 가까운 값을 가진다.
    
  • 위와 같은 경우 $R$ (Affinity Matrix)가 positive-semidefinte를 만족하지 못하지만, 논문 저자는 eigen-value 들이 cluster 크기를 나타내는데는 큰 문제가 없다고 한다.
  • 이러한 점에서 $\hat{S}^{'}$ 값을 이용해서 maximum eigengap를 계산하고, 최대 화자 수를 계산해 낸다.

Swtiching Strategy

• Inference 시에 Switch 라는 기법을 사용했다.
• Swtich 알고리즘
  • 1) 전체 EEND Embedding에 대한 EDA 를 시행한다. (기존 EEND-EDA와 동일)
  • 2) EDA에서 추출된 Speaker Attractor 수가 4명 미만인 경우, 기존 EEND-EDA 방법으로 Switch 하여 사용한다.
  • 3) 4명 이상인 경우 제안된 EEND-GLA를 사용한다.
• 개인적인 피드백
  • 많은 화자 수 상황(4명 이상)에서 Split이후 Clustering 하는 방법이 효과적이 었던거 같지만, 이보다 작은 경우에는 그냥 EEND-EDA를 사용하는 것이 더 좋았던 것으로 보임
  • LSTM에 전체 Embedding를 입력으로 넣어주어 생성된 local Attractor의 성능이 더 좋은 것으로 판단 됨

Experiments Result

Dataset

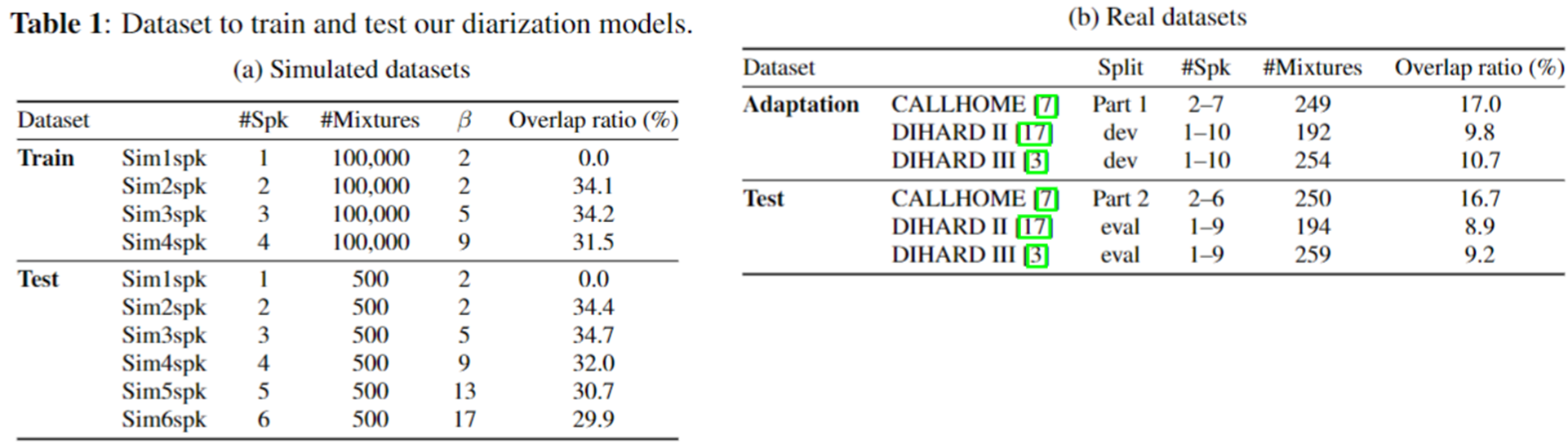
Training Strategy

• 1) Training
  • Training Sim2spk dataset 100 Epoch.
  • Funetuning Sim{1,2,3,4}spk dataset Each 50 Epoch.
  • Norm Scheduler: 100k

• 2) Adaptation
  • 100 epoch, lr: 1e-5

Experiment Results: Simulation Dataset

• 기존 EEND-EDA보다 대부분 좋은 성능을 보이는 것을 볼 수 있다.
• 5명으로 학습한 경우 EEND-EDA의 Sim5spk 성능은 이기지 못했지만, 대부분은 좋은 성능을 보인다.
• Local Loss 만으로 학습한 경우 Sim1spk에서 굉장히 불안한 모습을 보이며 (EDA의 불안정성으로 보임), Global Loss를 추가한 경우 좋은 성능을 보인다.
• Switch 방법을 사용하면 1,2명 화자 수에 대해서 성능 향상을 보여준다.
• Encoder Block 수를 늘리면 적은 speaker 수에 대한 성능 향상을 보이지만, 5,6명 화자수에 대해서는 성능 감소를 보인다.

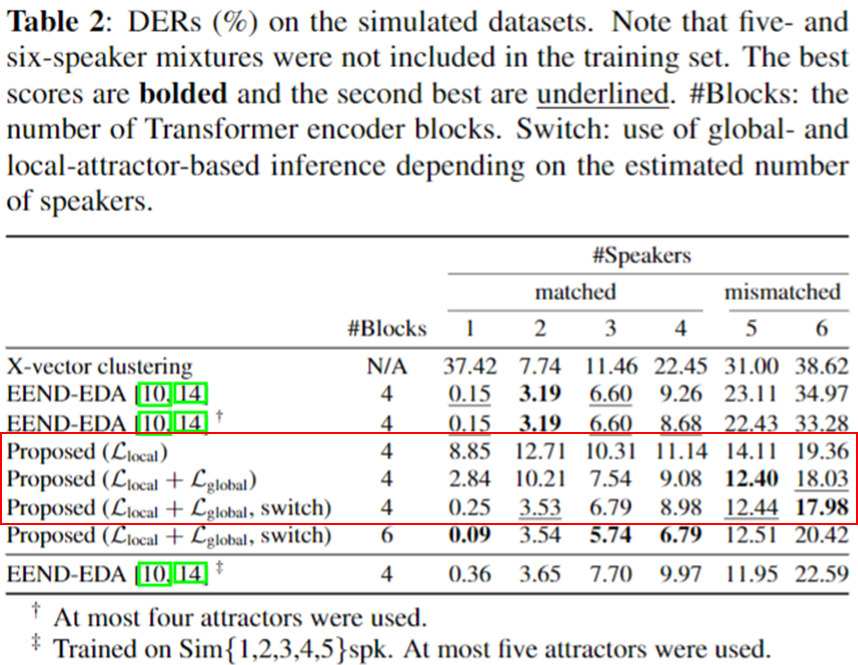
• EEND-EDA vs EEND-GLA
  • 확실히 5,6 명 상황에서는 더 좋은 성능을 보인다.
  • 1-4명 상황은 오히려 EEND-EDA가 안정적인 화자수를 보인다.

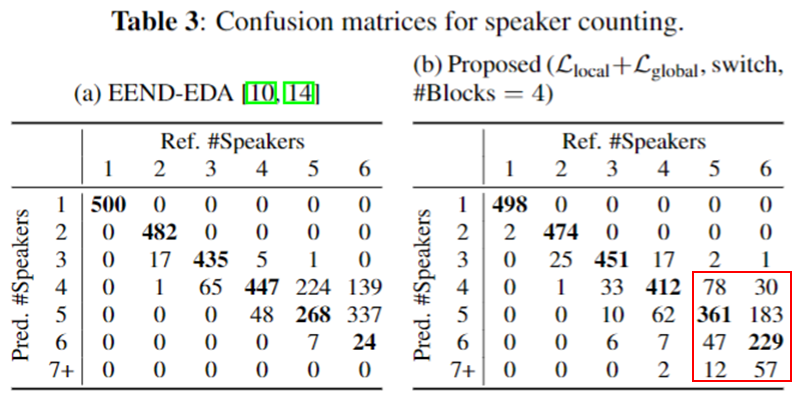
Experiment Results: CALLHOME Dataset

• 정확한 이유는 모르겠지만, Simulated Dataset 양상과 다르게 Encoder 개수를 늘린 것이 4명 이상 화자 수에 대해서 성능이 좋게 나오는 것을 볼 수 있다.
• SOTA 성능

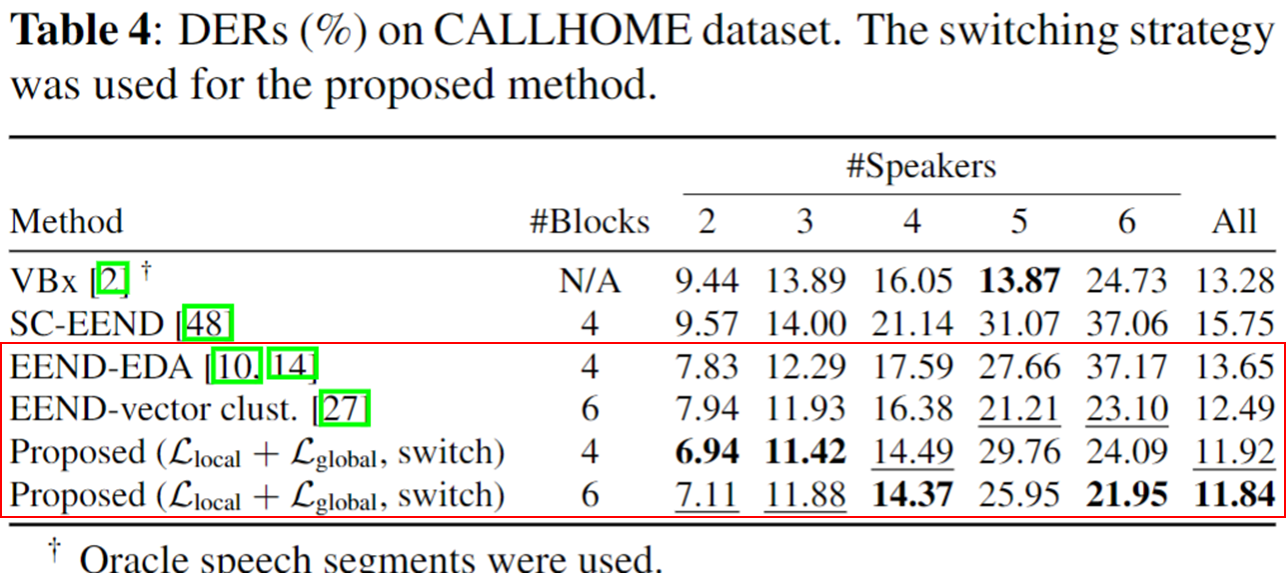
Experiment Results: DIHARD II, III Dataset

• 기존 EEND-EDA 보다 좋은 성능을 보이며, DIHARD III와 같은 경우 VBx 보다 좋은 성능을 보였다.

Conclusion

• EDA의 단점의 주목하고 이를 계선하려고 노력했다.
• Split 이후 Speaker Attractor 간의 Pairwise Loss를 추가하여 Clustering 를 시도했다.
• Transformer Decoder 이용해 효과적으로 global-local Attractor 를 생성했다.
• Multi-task를 적용하지 않고 최대한 Diarization에만 집중하는 모습이 어떤 면으로는 멋있는거 같다.