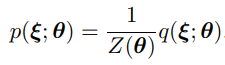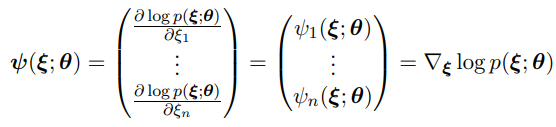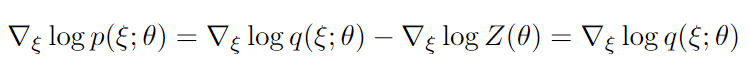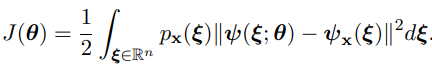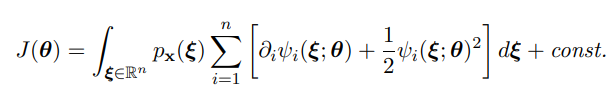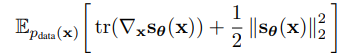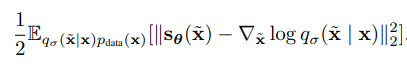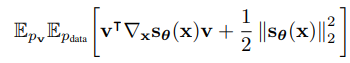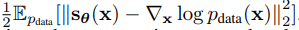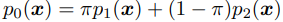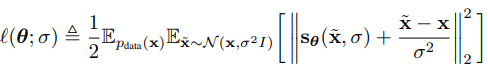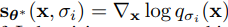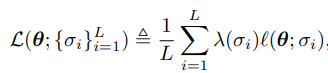1.Introduction

현대의 Generative model들은 크게 두 가지의 접근 방식을 가진다.

Likelhood-based method

Likelihood based method는 주어진 데이터 분포 $p_{data}(x)$를 근사하는 모델 $p_{\theta}(x)$를 학습시키는 것이 목표로, 주어진 학습 데이터 $x$에 대하여 모델의 (log-) likelihood $\log p_{\theta}(x)$를 최대화 하는 것을 목표로 한다.
대표적으로 VAE (Variational Autoencoder), (Normalizing-) flow등이 존재한다.

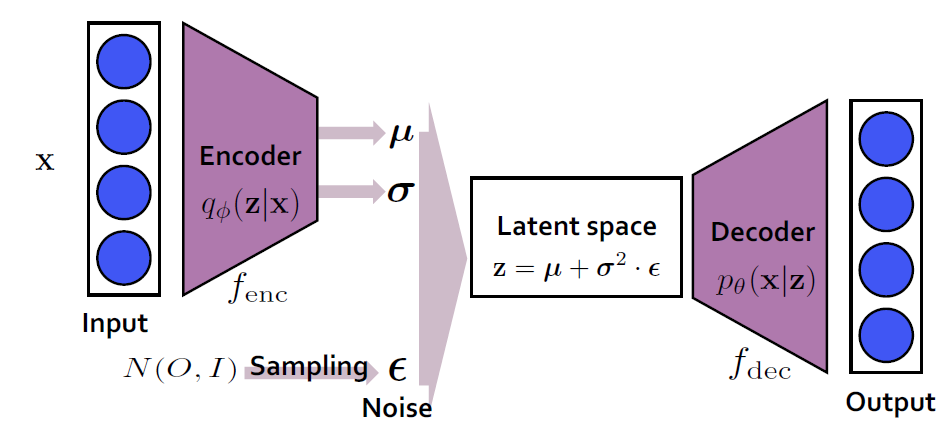
이러한 모델들이 갖는 문제점으로는 normalized probability를 모델링하기 위해 한정적인 모델 구조를 갖게 된다거나 (e.g. autoregressive models, flow models..) log-likelihood를 최대화하기 위해 간접적인 loss를 사용하여야 한다(e.g. ELBO for maximizing lower bound)는 것이 있다.

GAN-based method

GAN은 fake data를 만들어내는 Generator Network와 그것이 real data인지 fake data인지 식별하는 Discriminator Network로 구성되며, 서로간의 적대적 훈련을 통해 간접적으로 데이터의 분포를 학습한다.

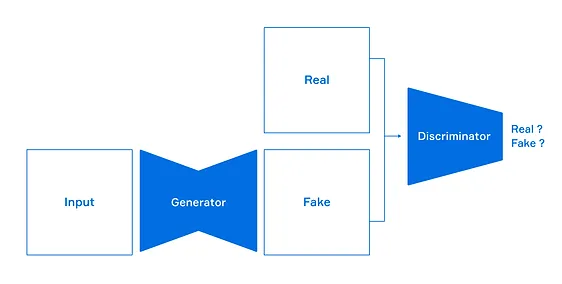
GAN이 갖는 문제점으로는 adversarial training을 하는 과정에서 unstability가 발생할 수 있으며, objective function이 없어 서로 다른 모델의 성능을 비교 평가할만한 지표가 없다는 것이다.

이 논문에서는 log-density function의 gradient로 정의되는 score function $\nabla_{\bold x} \log p_{data}(\cdot)$을 근사하는 모델 $s_{\theta}(\cdot)$을 학습하여 sample을 generate하는 모델인 score-based generative model을 제안한다.

Generating 과정은 score function에 의해 정의되는 vector field를 통해 Langevin dynamics을 구현함으로써 initial sample을 high density region으로 이끌어가는 과정으로 이루어진다.

하지만 score function을 구현하는 과정에서 현실적인 문제가 두 가지가 있다:

1.1. The manifold hypothesis

Manifold hypothesis는 real world data가 high dimensional space (i.e. ambient space)에 embed된 low dimensional manifold에 집중되어있다는 가설이다.

이 경우 ambient space에서 data point가 거의 존재하지 않는 부분에서는 $\nabla_{\bold x} \log p_{data}(\cdot)$가 정의되지 않을 수 있다.

또한 $\nabla_{\bold x} \log p_{data}(\cdot)$에 대한 estimator가 consistent한 결과를 내기 위해서는는 data distribution에 대한 support (=non-zero region)이 ambient space 전체가 되어야한다.

1.2. Low data density regions

data density가 낮은 영역의 경우 score에 대한 estimation이 부정확해지고, Langevin dynamics가 true data distribution에 수렴하는 속도가 느려진다.

따라서 이 논문에서는 data에 Gaussian noise를 가하여 data distribution의 부피를 키우고 dimensionality를 늘렸다. 이것이 low density region에서의 sample을 늘리는 효과를 주어 두번째 문제에 대해서도 도움이 되었다고 한다.

조금 더 핵심적으로, 두번째 문제를 해결하기 위해 여러 noise level에 대해 학습한 single score network를 통해 큰 noise level부터 점차 noise level을 줄여나가며 estimation을 모두 행하는 annealed version of Langevin dynamics를 제안하였다.

이렇게 했을 때 위의 모델들이 갖는 단점을 가지지 않으며, MCMC 샘플링 등의 approximation을 행하지 않아도 된다고 한다. 또한 다른 모델과 quantative하게 비교 가능하다고 한다.

2. Score-based method

흥미로운 주제이므로 Score matching에 대해서 조금 더 리뷰하고 들어가기로 한다.

이 세션의 내용은 Hyvärinen et al.의 "Estimation of non-normalized statistical models by score matching."의 내용을 전적으로 참고하고있음

Score matching은 원래 probabilistic model의 non-normalized density functuion 문제를 해결하기 위해 고안된 것으로, normalizing constanct의 intractible한 계산을 우회하기 위해 고안된 방법이다.

parametrized density model $p(\cdot;\theta)$을 통해 $p_{\bold x}(\cdot)$를 근사하는 모델 $p(\cdot;\hat\theta)$을 구하고 싶다고 하자.

일반적으로 우리는 probability density function $p(\xi;\theta)$에 비례하는 함수 $q(\xi;\theta)$까지는 찾을 수 있지만, 이를 통해 $p(\xi;\theta)$를 얻어내는건 쉽지 않다.

이는 고차원의 데이터에 대해 normalizing constant $Z(\theta)$를 계산하는것이 intractible하기 때문으로, $p(\xi;\theta)$에서 데이터를 샘플링을 하기 위해서는 $q(\xi;\theta)$에서 Markov Chain Monte Carlo (MCMC)등의 방법을 통해 샘플링을 하는 등의 간접적인 방법을 사용하여야 한다.

Score matching은 다음과 같이 정의된 score함수를 $\psi_{\bold x}(\cdot) = \nabla_{\xi} \log p_{\bold x}(\cdot)$에 근사시키는 것이 목적이다.

여기서 눈여겨봐야할 점은 $Z(\theta)$가 $\xi$에 독립적인 함수라는 것으로, 다음이 성립한다.

따라서 $Z(\theta)$에 대한 직접적인 계산 없이 다음과 같은 목적함수를 최소화함으로써 $\nabla_{\xi} \log p(\cdot;\xi)$ 를 $\nabla_{\xi} \log p_{\bold x}(\cdot)$에 근사할 수 있다.

하지만 저 함수의 계산을 위해 필요한 $\psi_{\bold x}(\cdot)$의 계산은 어떻게 되는걸까? 이 논문에서는 다음 등식을 통해 $J(\theta)$를 $\psi(\cdot;\theta)$만을 통해 계산할 수 있게 해준다.

여기까지 와서 의문이 든 사람도 있을 것이다. $\nabla_{\xi} \log p(\cdot;\xi)$ 를 $\nabla_{\xi} \log p_{\bold x}(\cdot)$에 근사시킨다고 하여서 $p(\cdot;\xi)$ 를 $p_{\bold x}(\cdot)$에 근사시킬 수 있을까?

이 논문에서는 위의 질문에 대해서도 답을 해준다.

2.1. Score matching for score estimation

이 논문에서는 $p_{\theta}(x)$를 모델링하여 이것의 score function을 matching하는것이 아닌, explicit한 score function $s_{\theta}(\cdot)$을 찾는 것이 목적이다.

위의 논문에서 보았듯 score funciton을 근사하는 모델 $s_{\theta}(\cdot)$을 구하기 위해서는 다음과 같은 objective function

을 최소화하는 $\theta$를 구해야 한다.

이 방법은 $Z(\theta)$의 직접적인 계산은 피했지만, 여전히 $p_{\theta}(x)$의 Hessian matrix $\nabla_{\bold x} s_{\theta}(\cdot)$를 계산해야한다는 점에서 computation에 부담이 가는 방법이다.

따라서 다음과 같은 두 방법이 large scale에서 주로 사용된다고 한다.

Denoising score matching

위의 논문에서 $\psi_{\bold x}(\cdot)$의 계산이 non-parametric estimation이므로 $\psi(\cdot;\theta)$만을 사용한 objective function을 대신 최적화한다고 이야기하였다.

Denoising score matching은 $\psi_{\bold x}(\cdot)$을 간접적으로 사용하기 위해 input $\bold x$에 대해 Gaussian distribution $q_{\sigma}(\tilde\bold x|\bold x)$을 만족하는 미세한 perturbed data $\tilde\bold x$를 만들어 다음을 최적화한다.

이는 gradient의 방향이 puterbed data $\tilde\bold x$로부터 input $\bold x$ 방향으로 흐를것이라는 직관에 의한 것으로, purterbation이 충분히 작다는 가정하에 hessian의 계산 없이 nearly optimal solution $\hat\theta$를 얻을 수 있다.

Sliced score matching

Sliced score matching은 직접적으로 score matching을 하는 대신, 랜덤한 방향에 대한 projection을 한 후 그 값을 평균내는 방식으로 간접적인 계산을 한다.

Sampling with Langevin dynamics

이 논문에서는 $p_{\theta}(x)$을 직접적으로 구하는 대신에 이렇게 얻어진 score function을 통해 Langevin dynamics를 구현하여 initial data $\bold x_0$로부터 $p_{\theta}(x)$를 따르는 데이터 $\bold x_T$를 다음과 같은 식으로 generate한다.

이 등식은 Stochastic Gradient Langevin Dynamics (welling & teh 2011)의 식에서 유래를 찾을 수 있다.

3. Challenges of score-based generative modeling

1번 섹션에서 간단히 언급하고 넘어간 것들이기 때문에, 자세히 언급하지는 않겠다.

3.1. The manifold hypothesis

위에서 말했듯, data manifold가 low dimensionality를 갖고있기 때문에 훈련이 불안정해진다.
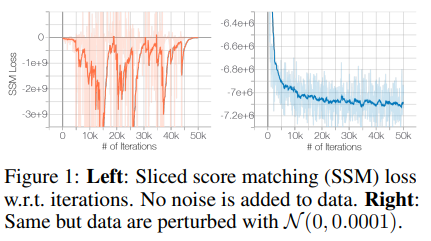
위의 표는 ResNet에서 CIFAR-10 데이터를 이용하여 score matching loss를 측정한 것으로, 인간은 인지조차 하기 힘든 0.0001 크기의 Gaussian noise를 가한것 만으로 훈련의 수렴 정도가 월등하게 좋아진 것을 알 수 있다.

3.2. Low data density regions

3.2.1 Inaccurate score estimation with score matching

Score matching은 다음과 같은 objective function을 최소화하는 알고리즘이라고 이야기했었다.

실제 학습 과정에서 이 expectation은 i.i.d sampled data들을 사용하여 계산을 하는데, data density가 낮은 영역에서는 이 값이 제대로 계산되지 않을 수 있다.

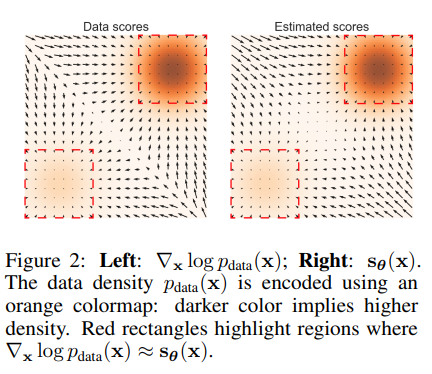
Fig.2는 toy example을 plot한 것으로, density가 높은 (색이 어두운) 영역의 경우 score function이 잘 근사되었지만, density가 낮은 (밝은) 영역의 경우 다소 gradient의 뱡향이 다른 것을 알 수 있다.

3.2.2 Slow mixing of Langevin dynamics

다음과 같은 bimodal distribution을 생각해보자.

이 때 두 확률분포 $p_1, p_2$가 disjoint할 경우 $\nabla\log p_0$은 $\nabla\log p_1$ 혹은 $\nabla\log p_2$의 값을 가지게 될것이다.

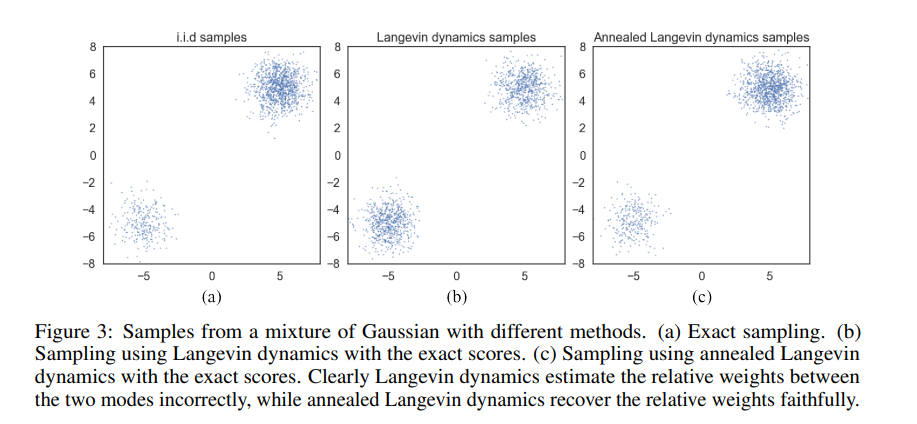
흥미로운 점은 각각의 score가 $\pi$와는 전혀 상관 없는 값을 가진다는 것이다. 다시말하여 $\nabla_{\bold x} \log p_{data}(\cdot)$만을 사용하여 sampling을 하는 Langevin dynamic의 경우 두 mode간의 relative weight을 회복하지 못할 수도 (= true distribution에 수렴하지 못할수도) 있다는 것이다.

실제 세계에서 Low-density region에 의해 가로막혀있는 bimodal distribution 또한 이에 가까운 모습을 보인다.

Fig 3.의 경우 Fig 2.에서 사용한 Gaussian mixture에 대해 Langevin dynamics과 Annealed Langevin dynamics을 구현한 것이다.

가운데의 경우 relative weight를 고려하지 않은 채 1:1의 비율로 샘플링이 이루어지고 있음을 알 수 있다.

4. Noise Conditional Score Networks: learning and inference

이 부분은 구체적인 구현에 관한 부분으로, 많은 디테일은 생략하겠다.

4.1. Noise Conditional Score Networks

Noise perturbation이 학습에 긍정적인 영향을 미친다는것은 위에서 충분히 언급하였다.
실제 구현을 할때는 각 noise level에 대해 각각의 score을 prediction하는 네트워크를 U-Net based model로 구현하였다고 한다.

4.2. Learning NCSNs via score matching

Score matching method는 위에서 언급한 두 방법이 모두 사용 가능하나, 문제의 set up이나 속도를 고려하여 denoising score matching을 사용하였다고 한다.
먼저, 각 noise level에 대해 matching objective

를 정하고, 각 noise level $\sigma_i$에 대해 weight $\lambda(\sigma_i)$를 부여하여 loss

를 최적화한다.

4.3. NCSN inference via annealed Langevin dynamics

위에서 언급했듯, Langevin dynaimics는 low density region이 존재할 경우 true posterior를 잘 포착하지 못하는 경우가 있다.

이 논문에서는 simulated annealing에 영감을 받아 각 noise level에 대해 순차적으로 Langevin dynaimics을 행한다.

이때 처음 단계에서는 large noise를 가하여 low density region이 줄어들고 high density 영역으로 빠르게 수렴한다. 그와 동시에 relative weight를 고려한 mixing이 빠르게 일어나고, 단계가 진행되면서 noise level이 줄어들어도 high density 영역에 수렴했으므로 계산이 정확하게 일어난다.

그리고 대충 성능이 기가막히다고 합니다. 와~