[ICLR 2017] TOWARDS PRINCIPLED METHODS FOR TRAINING GENERATIVE ADVERSARIAL NETWORKS

https://arxiv.org/pdf/1701.04862.pdf

Unstable GAN training with J-S Divergence

일반적으로, 우리는 Unsupervised learning을 할 때 데이터의 분포 $p_{data}$를 배우고자 한다.
많은 경우, 이것은 parameterized probabilistic model $p_{\theta}$의 $p_{data}$에 대한 (log-)likelihood를 최대화하는 (=KL-Divergence를 최소화하는) MLE 추정을 통해 이뤄진다.

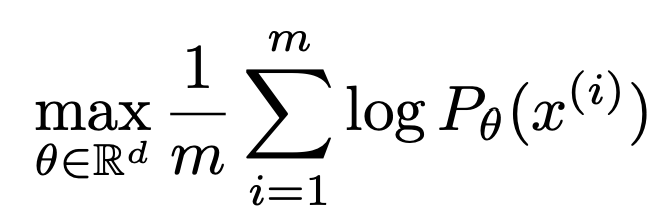
여기서 주목하여야 할 점은 KL-Divergence가 asymmetric하다는 것이다.

• $P_r > P_g$인 경우: 'Mode dropping'이라고 불리우는, 데이터의 특정 패턴을 generator가 학습하지 못하는 경우이다. 이 경우 generator가 커버하지 못하는 mode에 대해서 큰 cost를 준다. - 학습이 일어나는 부분
• $P_g > P_r$인 경우: generator가 데이터 분포가 dense하지 않은 부분에 큰 값을 할당하는 경우이다. 이 경우 fake-looking sample을 generate하는 것에 대해 작은 cost를 준다. - 학습이 잘 일어나지 않는 부분

반대로 $P_g$에 대한 $P_r$의 KLD를 최소화한다면 위의 관계가 반대가 될 것이고, fake-looking sample의 generation에 대해 penalty를 줄 수 있을 것이다.
따라서 GAN에서는 두 분포에 대해 symmetric한 penalty를 주기 위해 일반적인 MLE approach에서 사용하는 KLD 대신 Jensen-Shannon divergence를 사용한다.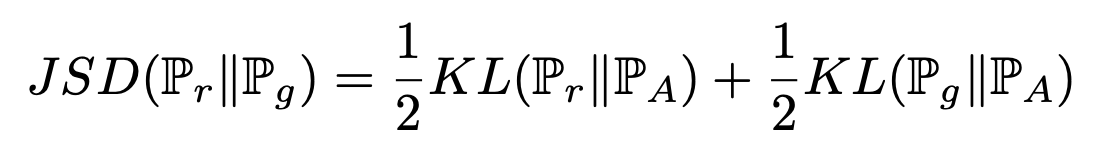

이 때 GAN의 Discriminator loss

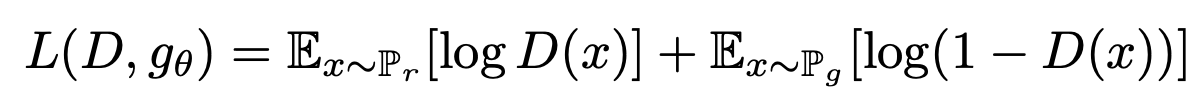
는 $D^*(x)= \frac{P_r(x)}{P_r(x)+P_g(x)}$일 때 최댓값

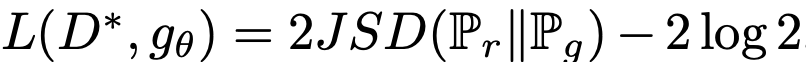
을 가진다. 따라서 Discriminator loss를 최소화하는 것은 discriminator가 optimal일 때 $P_r$과 $P_{g_{\theta}}$사이의 $JSD(P_r||P_{g_{\theta}})$가 Minimize되는 theta를 찾는 것과 같다.

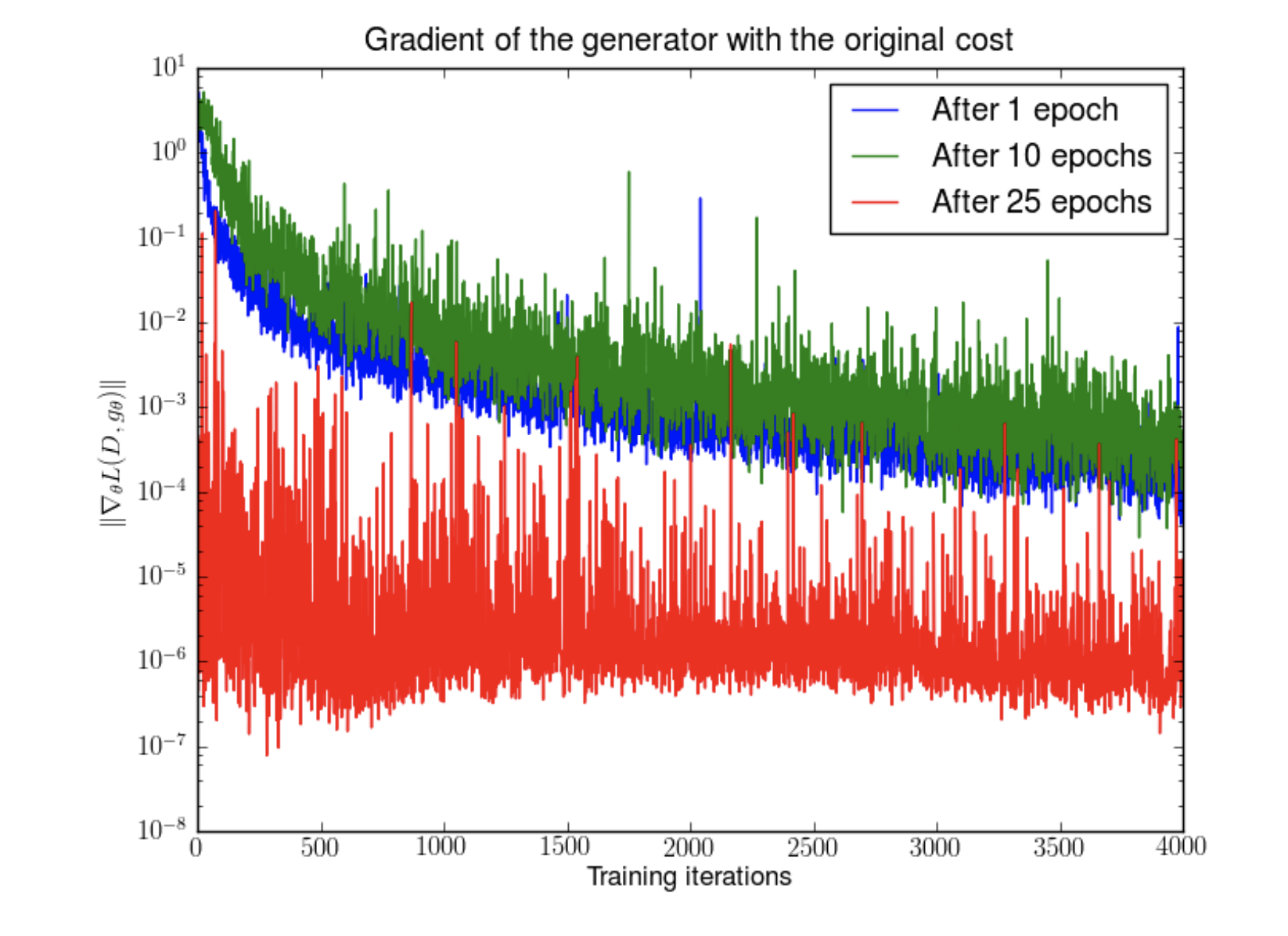
하지만 실제로 GAN을 학습시키면, (nearly) optimal한 D를 얻을수록 G의 업데이트가 점점 더 안좋은 방향으로 흘러가는 경우가 있다.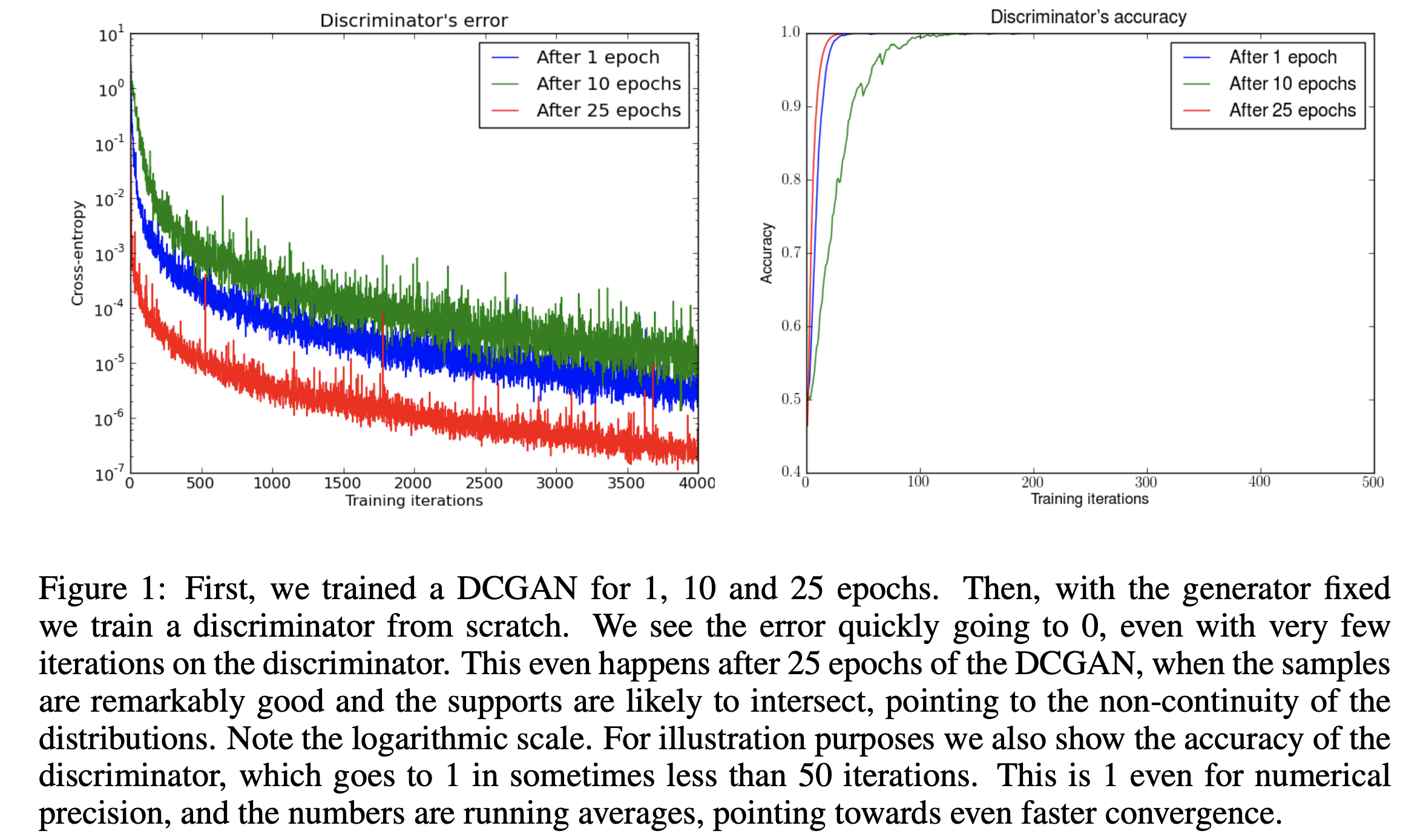 위 그림은 DCGAN의 학습 과정에서 1, 10, 25 epoch일 때 generator를 fix한 후 discriminator를 학습한 결과이다. 위에서 말한 이론적 upper bound

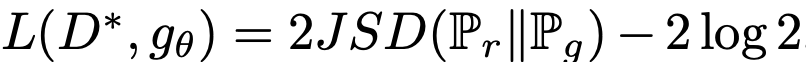
가 말하는 것과는 다르게, 실제로는 discriminator error가 매우 빠른 속도로 0에 수렴함을 알 수 있다. 이는

• $P_r$ 혹은 $P_g$ (혹은 둘 다)가 연속적이지 않거나
• 서로 다른 support (non-zero domain)을 가짐을 의미한다.

Source of instability

Low dimensionality of data manifolds

이론적으로 두 data manifold위의 확률 분포가 compact disjoint support를 가질 때 둘을 완전히 구분할 수 있는 smooth discriminator D가 존재한다는 것을 증명할 수 있다. 증명은 둘을 포함하는 compact set $\hat M,\hat P$를 잡고 Urysohn lemma를 통해 존재성을 보이는데, 거의 straightforward하다.

실제 data manifold의 경우 disjoint support를 가진다는 것을 쉽게 보장할 수는 없다. 하지만 두 manifold가 'transversal'한 교집합만을 가질 경우 (이를 저자는 'don't perfectly allign'이라는 표현을 사용하였다) 이와 유사한 결과를 가짐을 보인다.

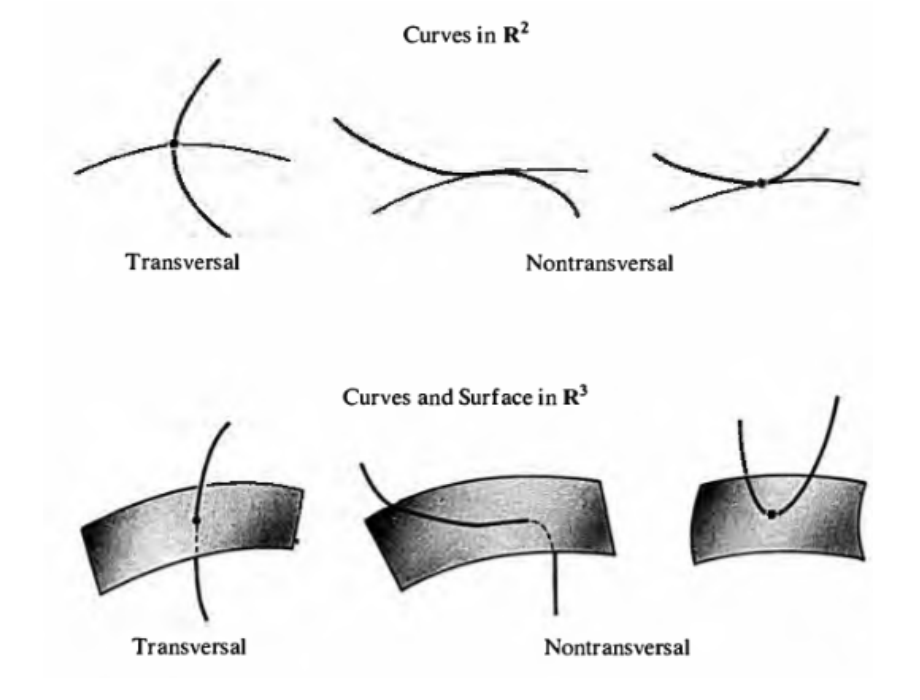
Transversal의 개념을 엄밀하게 정의하려면 미분기하의 지식이 필요하지만, 직관적으로 말하자면 '접하지 않는' 방향으로 만난다는 뜻으로 보면 된다. 위의 그림을 보면서 설명하자면, 각 곡선과 면(surface)이 접하는 방향으로 만날 경우 '접선'이 길이를 가질 수 있지만 (중앙 하단), 접하지 않는 방향으로 만날 경우 끽해봐야 '점'의 형태를 가지게 되어 길이를 가지지 않게 된다 (좌측 하단).

즉, transversal한 교집합은 '넓이'를 가지지 않는 교집합이므로 무시할 수 있다는 것이다.
논문에서는 데이터 manifold가 low-dimensionality를 가질 경우 almost sure하게 (= 1의 확률로) transversal한 교집합만을 가지고, 이 경우 두 확률 분포의 연속성에 의해 support가 disjoint함을 보인다.

증명은 위의 증명보다 조금 더 테크니컬한데 (compact support를 보장할 수 없으므로), 두 disjoint한 support를 포함하는 open set을 잡고 한 쪽에서는 1, 다른 한 쪽에서는 0인 step function 비스무리한 함수를 구성하여 증명한다.
여기서 중요한 점은 각 support에서 $D^*$가 상수함수라는 점인데, 이것이 backprop으로 generator를 학습하는 것을 불가능하게 만든다.

이를 조금 더 엄밀하게 보이자면 먼저 다음과 같은 Sobolev norm을 정의해야한다.

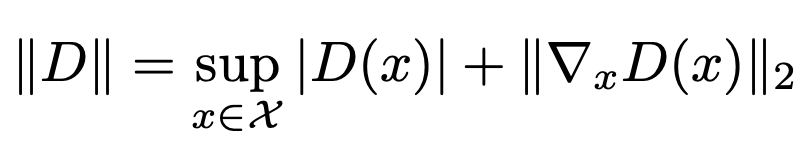
이 때 D가 'nearly optimal'한 경우 위와같은 low-dimensional case에서 vanishing gradient가 발생함을 알 수 있다.

즉 D가 optimal $D^*$에 가까워질 수록 theta에 대한 gradient의 크기가 작아진다는 것이고, 이것은 JS divergence의 minimization을 위해 optimal D를 얻어야 한다는 기존의 목표와 상충되는 결과이다.

이렇게 low-dimensional setting에서는 JS divergence라는 metric이 적절히 작동하지 않는 경우가 많다. 실제로 많은 논문에서 이미지 데이터 분포가 픽셀 차원보다 낮은 차원에 분포해있다는 점을 주장하고 있으며, GAN의 generator의 경우 low-dimensional latent space에서 sampling한 데이터를 고차원에 map하는 구조로 되어있어 저차원의 구조를 띠고있다.

The - log D alternative

JS divergence를 사용한 학습의 vanishing gradient 이슈가 불거지고나서 사람들은 다른 cost function을 사용한 학습을 선택했다. Negative log D alternative는 많은 사람들이 vanishing gradient문제를 피하기 위해 택한 optimization objective이다.

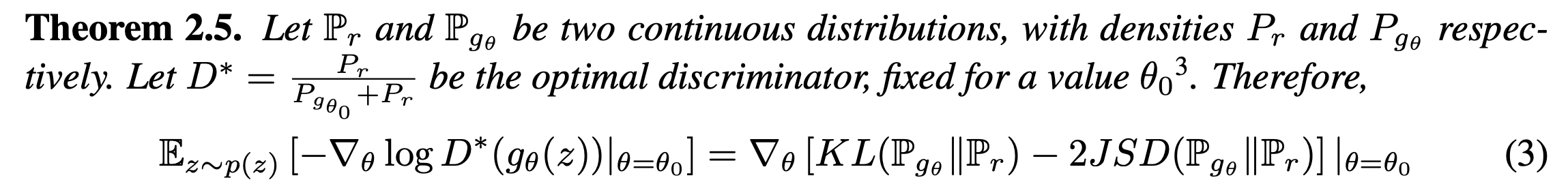
하지만 수식 (3)의 우항을 보면 알 수 있듯이, -JSD항이 포함되어있어 두 분포의 divergence를 증가시키는 방향의 업데이트가 포함되어있다.
$KL(P_g||P_r)$또한 MLE추정에서 사용하던 $KL(P_r||P_g)$이 아닌 반대 방향의 divergence이다.
위에서 지적한 대로 이 방향의 divergence는 fake-looking sample issue는 고려가 되지만 mode dropping issue는 고려가 되지 않는다. 이는 GAN이 실제로 좋은 품질의 이미지를 생성함과 반대로 mode dropping issue를 많이 겪는 이유중의 하나로 생각할 수 있다.

다음은 $D^*-D$, $\nabla_xD^*-\nabla_xD$가 x에 independent한, centered Gaussian process 라는 가정 하에 Negative log D를 사용할 때 gradient의 불안정성을 증명한 것이다.

증명은 간단한 chain rule을 사용하면 바로 나오는데, 분모가 $\epsilon$ (=centered Gaussian process)이므로 expectation을 취할 경우 무한으로 발산한다. 반면 분모가 0으로 수렴하지 않는다고 하면 gradient가 centered이므로 update가 0의 기댓값을 갖게 된다는 것을 의미한다.

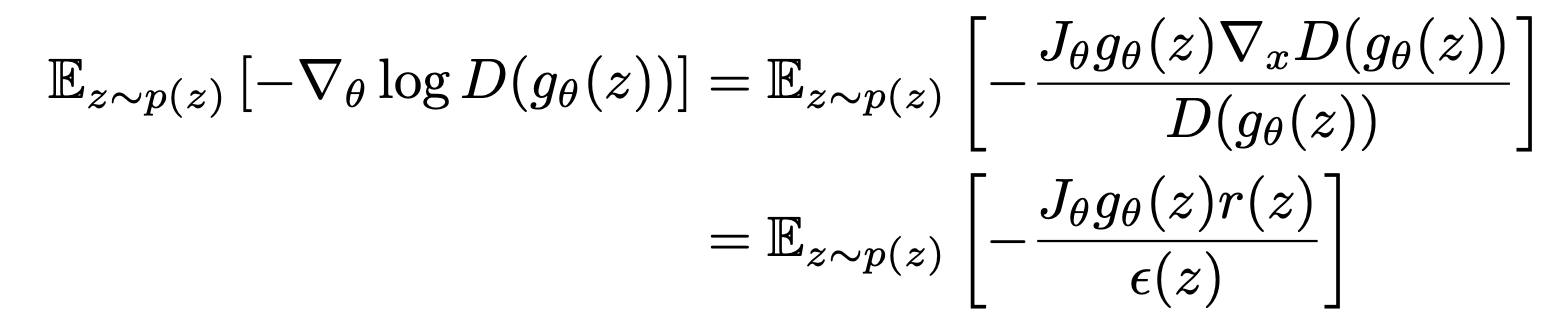
실제로 discriminator를 학습하면 할수록 grdient의 norm이 점점 커지는 것을 관찰할 수 있는데, 그 과정에서 norm의 variance도 같이 커지는 것을 볼 수 있다.

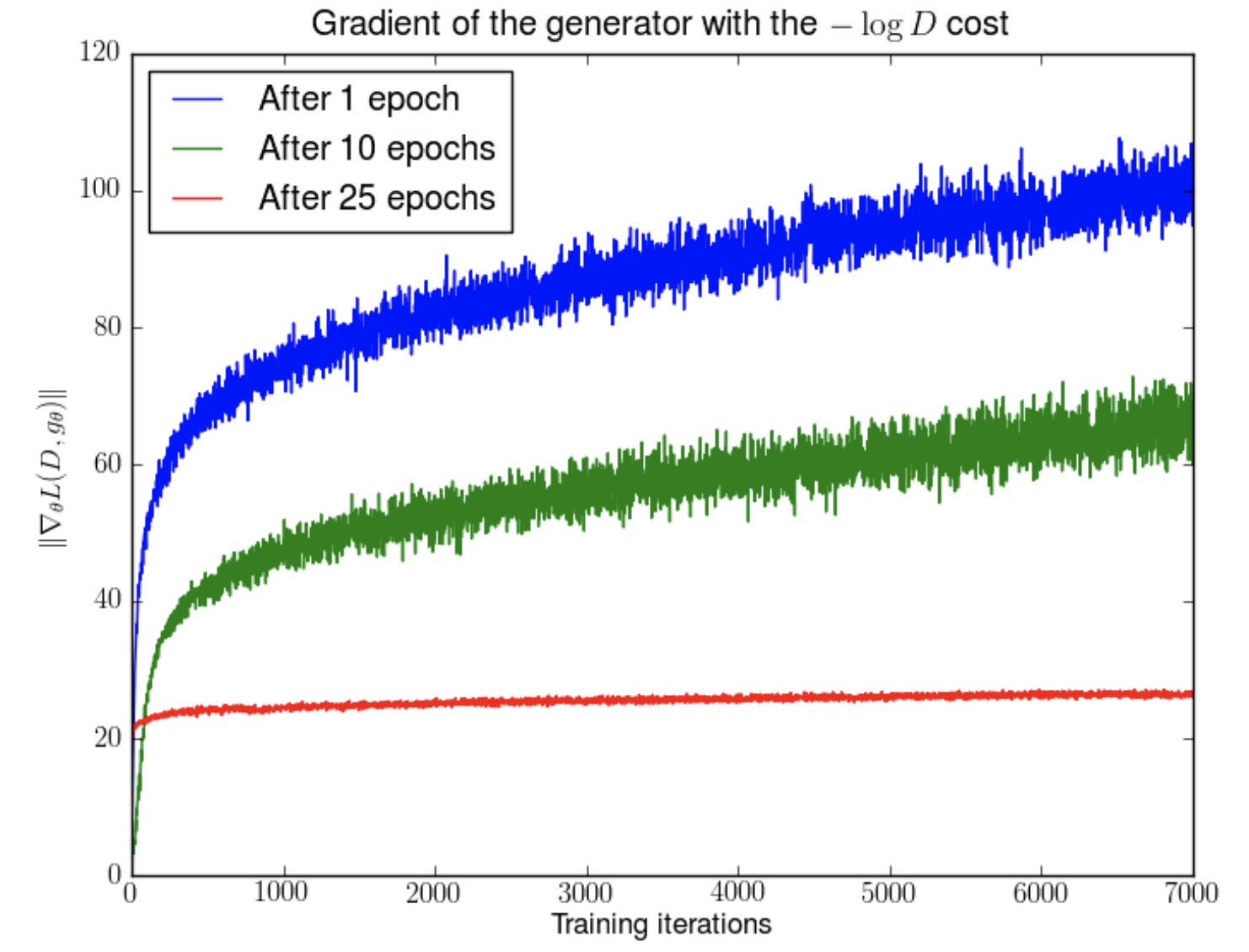
이와 같이 low-dimensional setting에서는 generator의 학습 과정에서 gradient가 instable한 행동을 보임을 알 수 있다. 또한 low-dimensionality로부터 나오는 중요한 성질이 하나 더 존재한다.

이는 $P_r, P_g$가 아무리 '가까이' 있어도 두 manifold가 low dimensionality를 가지면 divergence는 maximal한 값을 가질 수 있다는 것이다. 따라서 이 metric들이 low-dimensional data의 학습에도 적용될 수 있는 충분한 softness를 가지지 못한다고 한다.

Toward softer metrics and distributions

Training with noisy variants

그렇다면 이런 low-dimensionality 문제를 어떻게 하면 해결할 수 있을까? 많은 경우 이를 해결하기 위해서 input에 Gaussian noise를 주어 low-dimesionality를 해소하고자 한다.

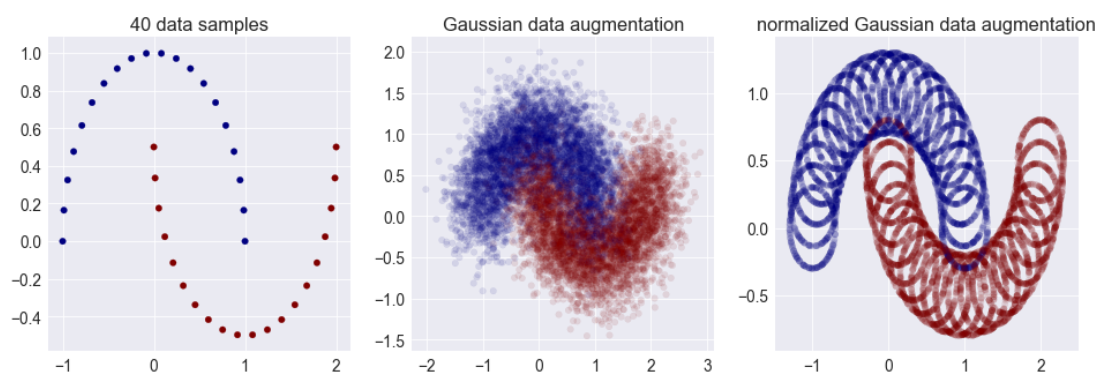
위의 사진을 보면, 각 클래스의 데이터 샘플들이 2차원 평면 위의 1차원 곡선 위에 분포해있는 형태를 띤다. 이 상태에서 2차원 Gaussian noise를 주면 데이터 분포를 '뚱뚱하게' 만들어서 2차원에 가까운 분포를 만들 수 있다. 이미지 데이터의 경우, 각 픽셀에 인간의 눈으로 imperceptible한 noise를 더하는 정도로도 충분한 dimension expansion 효과를 볼 수 있다.

이를 조금 더 엄밀하게 다루자면, 먼저 manifold $M$위의 확률변수 $X$와 노이즈 변수 $\epsilon$을 생각하자. 일반적인 Gaussian noise의 경우, 다음이 성립한다.

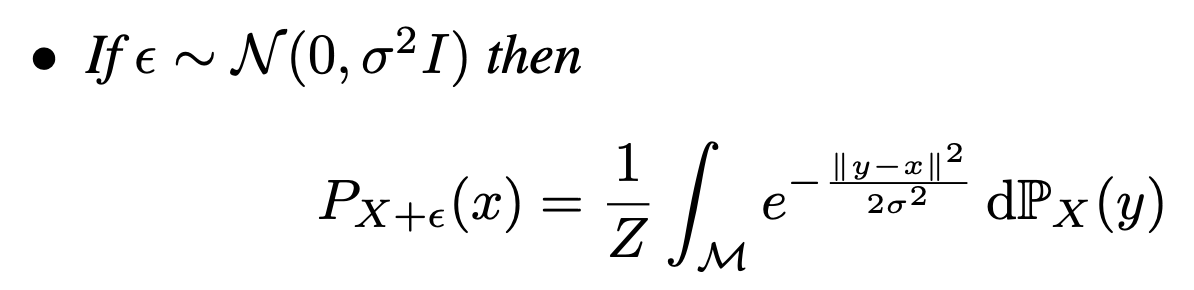
이는 smooth하게 X의 support를 확장하여 overlap을 강제로 만든 것으로 볼 수 있으며, 각 x에서 $\mathbb{P}_{X+\epsilon}$의 값은 각 data points 까지의 거리의 weighted sum에 반비례한다. Noise induction이후의 gradient는 다음과 같이 변한다.

식이 조금 복잡해보이기는 하는데, 조금 rough하게 말하자면 기존의 식에서 각 data points 까지의 거리의 weighted sum에 반비례하게 영향력이 adjust된 것이라고 보면 된다.
조금 더 자세히 뜯어보자면, 왼쪽 항은 real data manifold로부터 거리를 줄이려는 term이고 오른쪽 항은 fake data manifold로부터 거리를 벌리려는 term이다.
특히

• $P_g > P_r$인 경우 b>a가 되어 $P_g$를 낮추려는 방향의 update가 dominant해지고,
• $P_g = P_r$인 경우 두 term이 상쇄되어 gradient가 안정화된다.

문제는 discriminator의 input이 $g(z)$의 noisy variant $g(z)+\epsilon$인데 반해 generator의 update가 이뤄지는 부분은 0의 부피를 가지는 $g(Z)$이기 때문에 exact fake sample에 대한 discriminator의 update가 이뤄지지 않는다는 것이다. 심지어 g가 만드는 unreal한 데이터에 대해서도 cost를 높게 책정하지 않는 경우가 있다.

이를 해결하기 위해서 generator를 backprop하는 과정에서 또한 noisy sample을 사용하여야 한다고 주장한다. 이를 통해서 update가 negligible한 volume에서만 일어나는 것이 아닌 discriminator과 겹치는 영역에서 일어나게 할 수 있다.

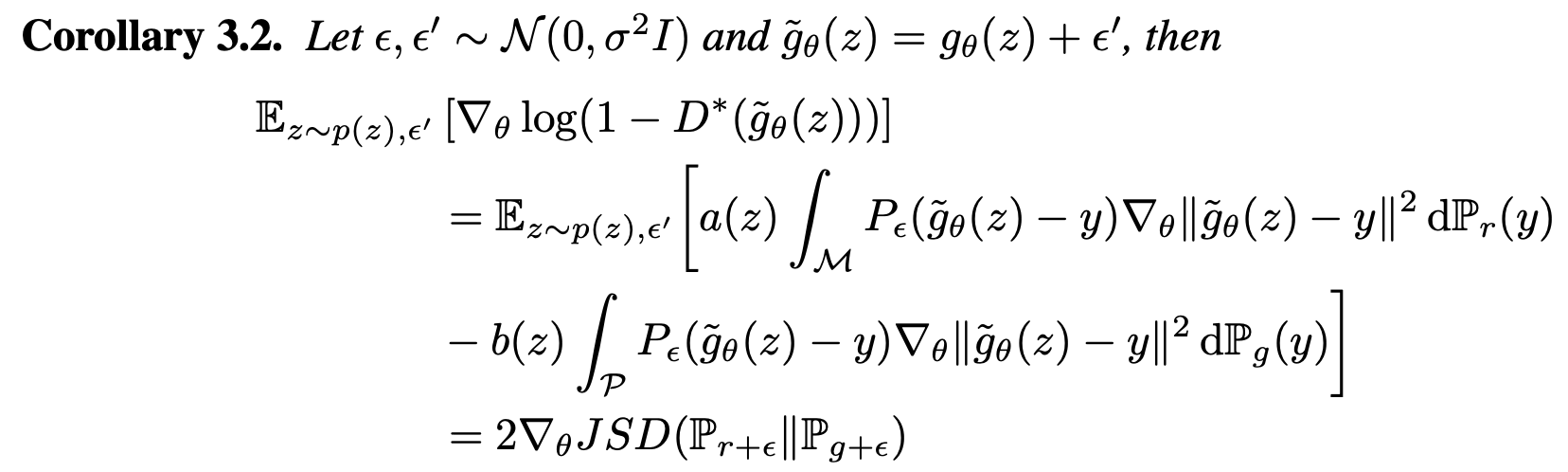
위 정리는 noisy variant에 대한 generator의 학습이 JSD와 어떻게 연결되어있는지를 보여준다. 각 noisy variant에 대해 학습하는 것은 noisy distribution끼리의 JSD를 최소화하는 것과 같다.

이 때 두 distribution의 거리가 가까우면 noisy distribution끼리는 거의 overlap하므로, original distribution에서 JSD가 maximized되는 경우에도 noisy variant간의 JSD는 작은 값을 보이게 된다.

Training with softer metric

위의 내용은 JSD를 probability function끼리의 divergence를 재는 metric으로 사용하기 위해 noisy variant of original distribution을 사용한다는 내용이었다. 하지만, 이 metric은 noisy variant간의 metric이지 두 probability function간의 intrinsic한 metric이 아니라는 한계가 있다.

저자들은 intrinsic한 divergence를 재기 위한 alternative measure로 Wasserstein distance(=earth mover's distance)를 제안한다.
Wasserstein distance를 설명하기 위해서는 transportation theory에 대해 간략한 설명을 해야 한다.

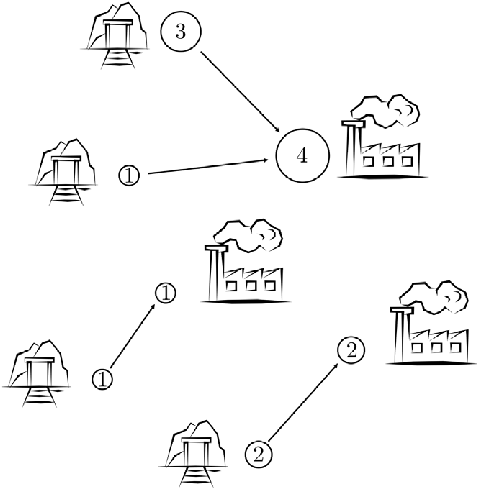
transportation theory를 설명하기 위해서 고전적으로 가장 많이 사용되는 예시는 mines-factories의 예시이다. 철강을 만드는 공장에 철광석을 운송하는 광산을 생각해보자. 각 철강 공장에는 수용할 수 있는 철광석의 양이 정해져있고, 각 광산은 철광석의 양과 공장까지의 거리에 따라 운송 비용이 달라질 것이다. Optimal transport는 어떻게 해야 운송 비용의 총합을 최소화하면서 철광석을 모두 공급할 수 있는지에 관한 이론이다.

또 다른 예시로는 흙 더미를 옮겨서 모래성을 만드는 예시가 존재한다. 흙 더미를 멀리 옮길수록, 많은 양의 흙더미를 퍼 옮길수록 에너지 소모가 클 것이고, 우리는 에너지 소모가 가장 작은 선에서 모래성을 만들고 싶다.

$x$좌표에서의 높이가 $h(x)$미터인 흙 더미가 있다고 생각하고, $x$좌표에 있는 흙 더미 1미터를 $x'$까지 옮기는 데에 드는 에너지가 $c(x,x')$라고 하자. 이 때 특정 위치의 흙 더미를 나눠서 옮길 수 없다고 가정하면 x좌표의 흙더미를 $x'$까지 옮기는 데에 드는 비용은 $h(x)c(x,x')dx$가 될 것이다.

모래성을 만들기 위해서는 흙 더미의 어느 부분을 어디로 옮겨야 할 지에 대한 계획 (transportation plan) $T:X \to X'$를 세워야 할 것이다. 그렇다면 우리가 찾는 최적의 계획 (optimal transport plan) $T^*$는 각 흙더미를 옮기는 비용의 총 합 $\int_Xh(x)c(x,T^*(x))dx$를 최소화 하는 $T$가 된다.

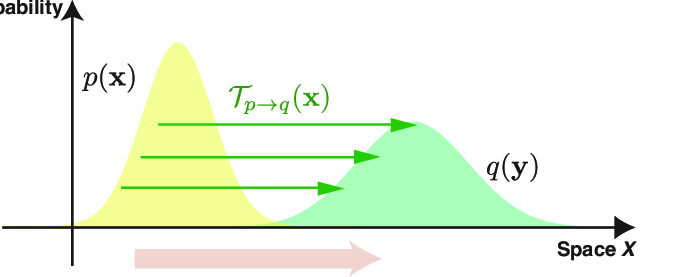
서론이 길었는데, transportation theory를 이렇게 길게 설명한 이유는 '흙더미를 옮기는 최소 비용'이 사실은 '확률 분포를 옮기는 최소 비용'에 대한 비유로써 사용할 수 있기 때문이다.
'흙더미의 높이'를 '특정 위치에서의 확률밀도'로 해석하게 되면 확률 분포를 다른 분포로 옮기기 위해 얼마나 많은 비용이 필요한지를 측정할 수 있게 되고, 이 비용의 크기를 두 분포가 얼마나 멀리 떨어져있는지에 대한 distance metric으로써 해석할 수 있게 된다.
특히 cost function c가 단순한 Eucldian distance가 될 경우, 이 때의 transportation cost를 Wasserstein metric, 혹은 더 직접적으로 earth mover's distance라고 부르는데 (물론 엄밀한 의미에서의 distance는 아니다) 이는 위의 '흙 더미 옮기기'의 예시를 생각했을 때 꽤나 적절한 이름이라고 할 수 있다.

Euclidian distance가 포함된 점에서 눈치챈 사람도 있겠지만, 이 metric은 두 분포의 support간의 직접적인 overlap이 없어도 distance를 충분히 정의할 수 있다. Low-dimensional setting에서 JS Divergence의 경우 아무리 작은 noise level을 가져도 확률분포 $\mathbb{P}_X$ 와 이것의 noisy variant $\mathbb{P}_{X+\epsilon}$에 대해서 maximal divergence를 갖는데 반하여 Wasserstein metric은 $\epsilon$의 Variance에 의한 upper bound를 갖는다. (증명은 straightforward하니 굳이 언급하지 않겠다.)

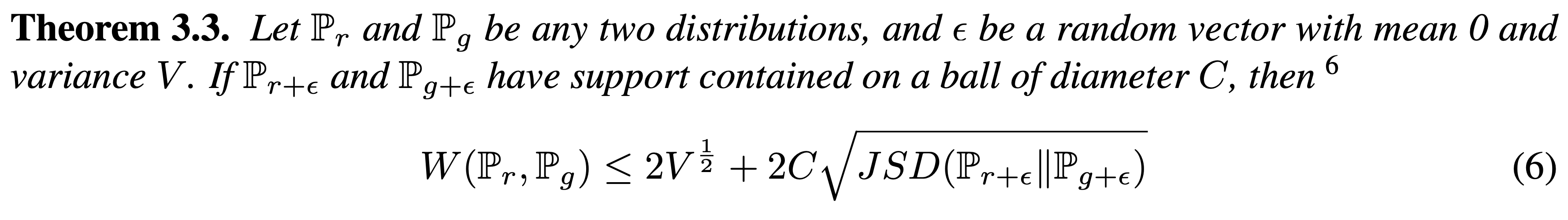
이를 이용하면 Wasserstein metric과 JSD with noisy variant 간의 관계에 관한 정리를 얻을 수 있다.
중요한 것은 오른쪽 항이 $\epsilon$의 variance에 대한 조절과 GAN의 학습에 의해 조절될 수 있다는 점으로, noisy variant에 대한 학습이 Wasserstein distance의 minimization을 가져온다는 점이다.

이 아이디어가 발전해서 후속논문인 Wasserstein GAN이 나왔는데, 사실 그 논문에서 든 예시보다 이 논문에서 보여준 내용이 조금 더 Wasserstein metric의 사용을 정당화하기에 적절하지 않았나..싶기도 하다. 그 내용은 분량상 따로 정리하도록 하겠다.